Normal Distribution
The Normal (or Gaussian) distribution is the most common type of probability density function (PDF), and is often used for probabilistic studies in geotechnical engineering.
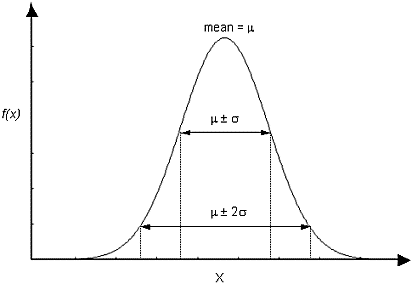
For a Normal distribution, about 68% of observations should fall within one standard deviation of the mean, about 95% of observations should fall within two standard deviations of the mean, and over 99% should fall within 3 standard deviations.
Normal probability density function, showing standard deviation ranges
Truncated Normal Distribution
A truncated Normal distribution can be defined by setting the desired minimum and/or maximum values for the variable. If the minimum / maximum values are less than 3 standard deviations away from the mean, the distribution will be visibly truncated. For practical purposes, if the minimum and maximum values are at least 3 standard deviations away from the mean, you will obtain a complete normal distribution.
Estimating a Standard Deviation
For a theoretical Normal distribution, 99.73 % of all samples, will fall within 3 Standard Deviations of the mean value. This fact leads to the following rule of thumb (the "Three Sigma Rule"), which allows you to estimate a standard deviation for a normally distributed random variable.
Estimate the highest conceivable value (HCV) of the random variable, and the lowest conceivable value (LCV), and divide the difference between them by six:
![]()
The resulting value can be taken as the Standard Deviation of the Normally Distributed random variable. This is useful if actual data is not available. This and other methods of estimating standard deviation, are discussed in (Duncan, 2000).