Fisher Distribution
A Fisher Distribution is commonly used for modeling the distribution of 3-dimensional orientation vectors [Fisher (1953)], such as the distribution of joint orientations (pole vectors) on a sphere. A Fisher Distribution describes the angular distribution of orientations about a mean orientation vector, and is symmetric about the mean. The probability density function can be expressed as:
![]() Eqn.1
Eqn.1
where ![]() is the angular deviation from the mean vector, in degrees, and K is the "Fisher constant" or dispersion factor.
is the angular deviation from the mean vector, in degrees, and K is the "Fisher constant" or dispersion factor.
In RS2, joint orientations for the Baecher or Veneziano joint network models can be defined using a Fisher distribution.
Fisher K
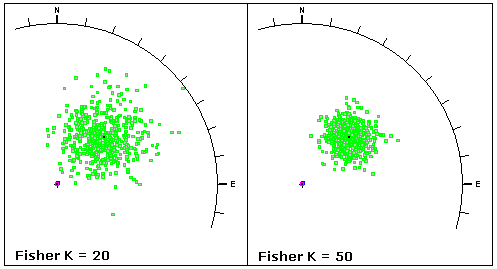
The Fisher K value describes the tightness or dispersion of an orientation cluster. A larger K value (e.g. 50) implies a tighter cluster, and a smaller K value (e.g. 20) implies a more dispersed cluster, as shown in the following figure.
Stereonet plots showing the effect of Fisher K on a randomly generated joint set of 500 samples
The Fisher K value can be estimated from Eqn. 2, for data sets with greater than approximately 30 vectors (poles) [Fisher (1953)].
![]() Eqn.2
Eqn.2
where N is the number of poles, and R is the magnitude of the resultant vector (i.e. the magnitude of the vector sum of all pole vectors in the set).
Standard Deviation
By analogy with a Normal distribution, it can be shown that the standard deviation of a Fisher distribution can be estimated from Eqn.3 [Butler (1992)].
![]() Eqn.3
Eqn.3
where ![]() is the "angular standard deviation" or "angular dispersion" of the Fisher Distribution, and K is the Fisher constant.
is the "angular standard deviation" or "angular dispersion" of the Fisher Distribution, and K is the Fisher constant.