Generalized Anisotropic

The Generalized Anisotropic Strength model allows you to define Anisotropic strength properties for a material using any combination of failure criteria applied over user defined orientations. There are two methods of defining the anisotropy:

• Dip/Dip Direction - you can define one or more planes of anisotropy, with 3-dimensional orientation defined by Dip and Dip Direction, OR
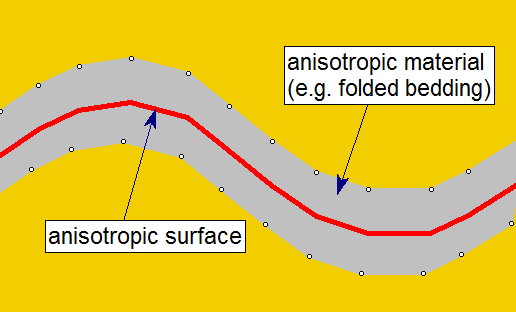
• Surface - you can define a general 3D anisotropic surface (e.g. to follow the orientation of folded bedding strata).

Each anisotropic plane or surface can be assigned its own failure criterion, within a specified angular range defined by A and B parameters. The rock mass is also assigned a failure criterion. The strength of any failure plane through the anisotropic material can then be calculated, using a linear interpolation method, as described below.

To define a Generalized Anisotropic Strength Function:

1. Set the Failure Criterion: Anisotropic > Generalized Anisotropic in the Material Properties dialog.
2. Select the Edit button beside the failure criterion combo box.
3. You will see the Define Generalized Strength Function dialog.
   • To edit an existing Generalized Anisotropic Strength function, select the Function Name from the list at the left of the dialog.
   • To create a new Generalized Anisotropic Strength function, select the Add button at the lower left corner of the dialog, and enter a Function Name.
4. Select the Base Material for the function. This will represent the strength properties of the rock mass, for failure planes which are not within the defined orientation range of the anisotropic plane(s) or surface.
5. Select the Anisotropy Definition - Dip/Dip Direction or Surface. For each plane or surface, assign a material and enter the required parameters as described below.
6. When all data has been entered, select OK, and you will be returned to the Material Properties dialog. The Name of the function you have just defined will appear in the Generalized Function list. By selecting a Function Name from this list, you can now apply a Generalized Anisotropic Function to any material in the model.
   
In the Material Properties dialog you must also define the material strength properties for the rock mass and anisotropic plane(s) assigned in steps 4 and 5.

Anisotropy Definition - Dip/Dip Direction

The Anisotropy Definition = Dip/Dip Direction option allows you to define one or more planes of anisotropy, with orientation defined by Dip and Dip Direction. The A and B parameters define the angular range of the anisotropy as described below.

1. By default, one anisotropic plane will be defined. Enter the Dip and Dip Direction of the anisotropic plane, and enter the A and B parameters (see below for details), and select a Material for the anisotropic plane.
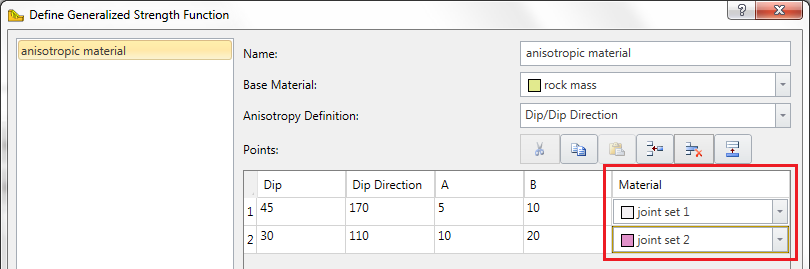
2. If you have more than one anisotropic plane, select the Insert Row button to add the required number of rows. Enter the Dip, Dip Direction, A and B parameters for each plane. 2-Dimensional representation of two anisotropic plane orientations.

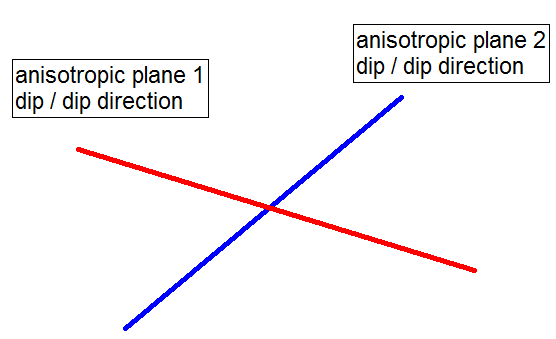
Definition of Dip/Dip Direction

The definition of Dip and Dip Direction follows the standard convention:

• Dip Direction is measured from the North, with clockwise positive convention. The y-axis of your model represents the North direction.
• Dip is measured from the horizontal, with downward positive convention.

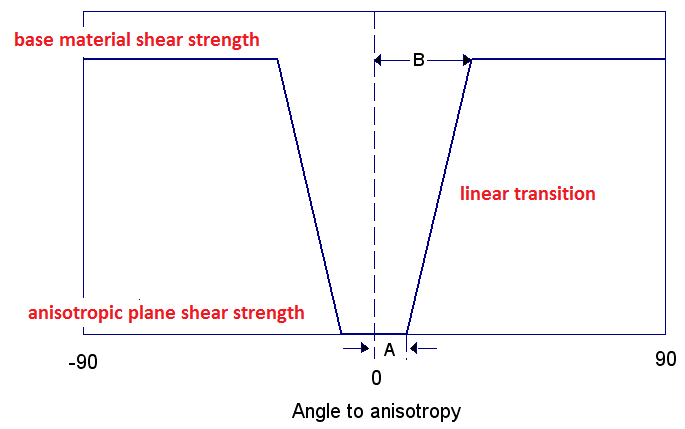
Definition of A and B Parameters for Generalized Anisotropic Function

The definition of the input parameters for the Generalised Anisotropic strength model is described below. For example, let's assume a rock mass has a single well-defined plane of anisotropy, such as a bedding plane, with input as shown below.

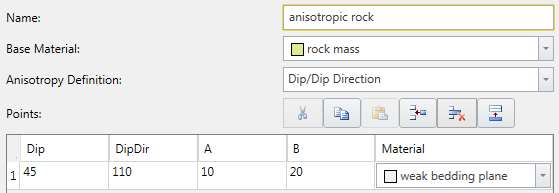
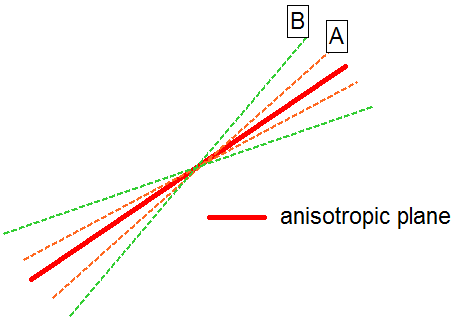
A 2D representation of the A and B parameters is shown below. If a shear plane (column base) lies within the A angle, the anisotropic plane strength is applied. If a shear plane lies outside of the B angle, the rock mass strength is applied. If a shear plane lies between the A and B angles, a linear transition between the rock mass strength and the anisotropic plane strength is applied.

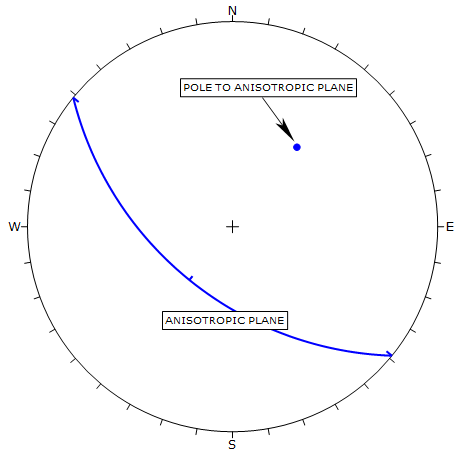
The best way to illustrate the definition of the A and B parameters is within the aid of a stereonet. The 3-dimensional orientation of an anisotropic plane is given by entering the Dip and the Dip Direction of the plane. On a stereonet, a plane can be represented as a great circle with corresponding pole (normal vector) as shown below.

The A and B parameters define the angular radius of two cones centered on the pole vector of the anisotropic plane, as shown in the following figure.

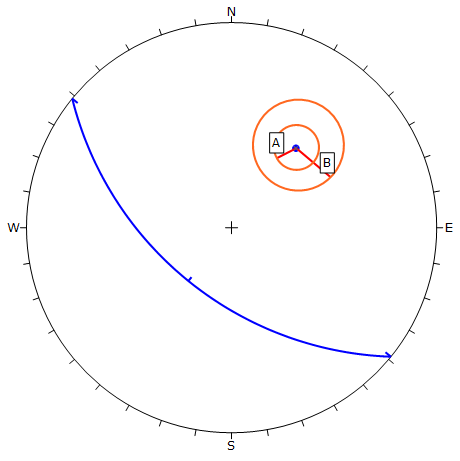
Definition of A and B Parameters for Anisotropic Plane

The Generalized Anisotropic Strength model is applied as follows. For a given column in a sliding mass, the orientation (dip and dip direction) of the base of the column is determined. The normal vector to the base of the column is then determined.

• If the normal vector of the column base is WITHIN radius A of the normal vector of the anisotropic plane, then the strength model selected for the Anisotropic Plane is applied (in the above example the "weak bedding plane" material).
  
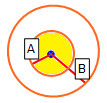
• If the normal vector of the column base is OUTSIDE radius B of the normal vector of the anisotropic plane, then the strength model selected for the Base Material is applied (in the above example the "rock mass" material).
  
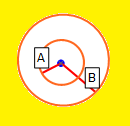
• If the normal vector of the column base is OUTSIDE radius A and WITHIN radius B, then the strength applied is based on a linear transition between the Anisotropic Plane strength and the Base Material strength, as shown in the figure below.
  

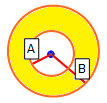
The following figure illustrates how the shear strength is derived for a Generalized Anisotropic material. Within angular radius A the shear strength of the anisotropic plane is applied. Outside of angular radius B the base material (rock mass) strength is applied. For angles between A and B the transition of shear strength is assumed to be linear.

Anisotropic Strength Properties from RS2 to RS3

In RS2, anisotropic strength properties are assigned with simple angular measurement. Since RS2 does not contain 3D orientation of the planes with weakness defined by dip and dip direction, there are few assumptions when creating a 3D model from a 2D model with the anisotropic strength properties. Firstly, dip direction is aligned to the East-West direction. This is due to 2D model extruded along the north direction. The angular range is then converted to Dip and A and B factors.

Here are the rules for importing and converting a RS2 generalized anisotropic function:

1. The material with the maximum cumulative angular range in 2D is defined as the base material in 3D.
2. All other materials that are part of the 2D generalized anisotropic description are translated as Anisotropic directions in 3D.
3. The 3D dip is equal to the 2D (Angle From + Angle To)/2.0
4. The A value is equal to the 2D (Angle To - Angle From)/2.0
5. B value is A + 5 degrees

Dip and Dip direction are always adjusted so that Dip is positive.

Multiple Anisotropic Planes

If more than one anisotropic plane has been defined, the algorithm first determines which anisotropic plane is nearest to the orientation of a given column base. The the calculation proceeds as described above, only considering the nearest anisotropic plane. Other anisotropic planes are ignored.

Anisotropic Definition - Surface

The Anisotropy Definition = Surface option allows you to assign a surface which corresponds to the mean orientation of a non-planar anisotropic region. For example, as illustrated in the figure below. For simplicity this is illustrated in 2D, however, the actual surface is 3-dimensional.

In order to use this option:

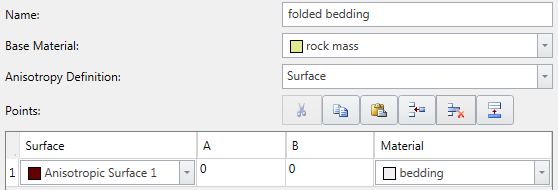
1. You must first define the Anisotropic Surface using the Anisotropic Surfaces option in the Surfaces menu.
2. You will then be able to assign this surface to the Generalized Anisotropic material, with A and B parameters.

The Anisotropic Surface option is useful because it allows you to assign a single anisotropic material type, to a non-planar material zone with variable anisotropic orientation. The Anisotropic Surface option is useful because it allows you to assign a single anisotropic material type, to a non-planar material zone with variable anisotropic orientation. The determination of shear strength is exactly the same as described above for the planar Dip/Dip Direction option, with the following additional step:

• For a given column base, the NEAREST point on the Anisotropic Surface is first determined.
• This gives a local value for the Dip/Dip Direction of the anisotropic surface.
• The angle between the column base plane and the local anisotropic surface orientation is determined.
• The calculation of shear strength for the column base, then proceeds as described above for the planar Dip/Dip Direction option.

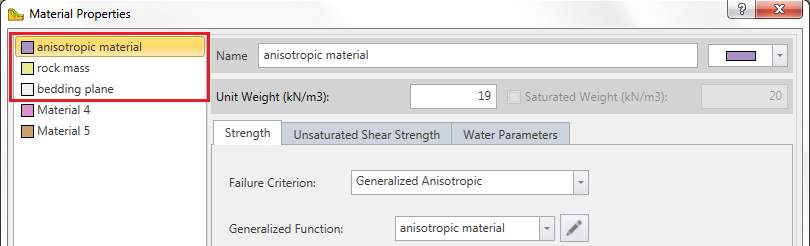
Generalized Anisotropic Material Assignments

A Generalized Anisotropic material in RS3 will always require at least three material assignments:

1. One material for the Generalized Anisotropic material.
2. One material for the rock mass strength assignment.
3. One material for the anisotropic plane or surface strength assignment.

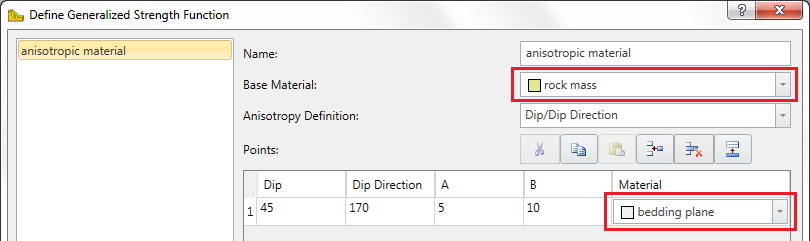
The Generalized Anisotropic material is really a composite material with a rock mass strength component and one (or more) anisotropic strength component(s). If the Anisotropy definition = Dip/Dip Direction, and more than one anisotropic plane is defined, then each plane may have a different material assigned. This is illustrated below.

Failure Criteria for Base Material and Anisotropic Planes

You may use any material strength model for the base material (rock mass) and anisotropic planes. For example, you might use:

• Generalized Hoek-Brown (for the rock mass)
• Barton-Bandis (for anisotropic planes or surface)

You are not limited to Mohr-Coulomb strength model when using the Generalized Anisotropic material option in RS3.

Tensile Strength

See the Tensile Strength topic.