Stiffness Properties

The following elastic models are available for defining your material stiffness (elastic) properties in the Material Properties dialog:

• Linearly Isotropic
• Transversely Isotropic
• Orthotropic
• Duncan-Chang Hyperbolic
• Non-linear Isotropic
• Custom
• Datum Dependent

An unloading condition can be specified by selecting the Use Unloading Condition checkbox and selecting the condition from the dropdown list (e.g. Mean Stress, Deviatoric Stress, Volumetric Strain, Deviatoric Strain).

Linear Isotropic

A Linear Isotropic material implies that the material properties do not vary with direction. The elastic properties of an Linear Isotropic material are defined by a single value of Young’s Modulus and a single value of Poisson’s Ratio.

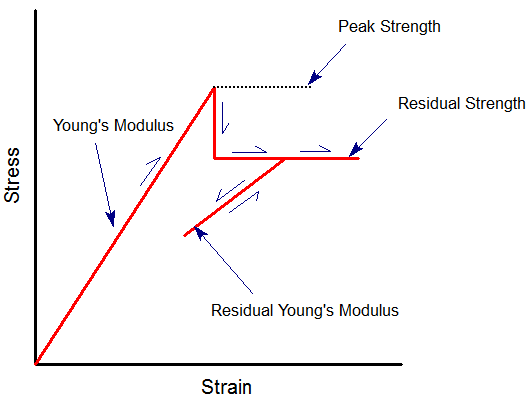
Residual Young's Modulus

For a Linear Isotropic material you can define a residual value of Young's Modulus by selecting the Young's Modulus (residual) checkbox. This option is only enabled if the failure criterion = Mohr-Coulomb, Hoek-Brown, Drucker-Prager, or Generalized Hoek-Brown. The residual value of Young's Modulus will be used in the analysis under the following conditions:

• Material yielding has occurred (peak strength envelope exceeded)
• After yielding, the material is subjected to a change in load state (i.e. unloading / reloading).

Only under these conditions will the residual modulus be applied. If the material yields but the load state does not change, then the residual modulus will not be applied. This is indicated in the following figure.

Definition of residual Young's modulus

Transversely Isotropic

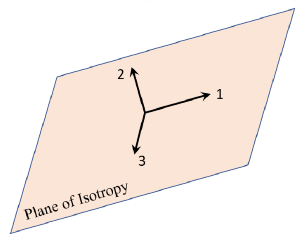
A Transversely Isotropic material has properties that vary with direction. The elastic properties are specified in two orthogonal directions as follows:

• E1 and E2 are the values of Young's Modulus in two orthogonal directions
• E3 = E1 therefore plane 1-3 is the isotropic plane
• The orientation of E2 is specified by XYZ vector components where XYZ corresponds to the principal axes of your model. The orientation of E2 is normal to the isotropic plane 1-3
• The required Poisson’s ratios are v12 and v13 = v31 = v. Note that vij implies strain in the j-direction due to strain in the i-direction. Also note that Ei / Ej = vij / vji
• G12 is the shear modulus in the 1-2 plane
  
  

Orthotropic

An Orthotropic material has properties that vary with direction. The elastic properties are specified in three orthogonal directions.

• For an Orthotropic material three Young's moduli are required: E1, E2 and E3
• Three Poisson’s ratios are required: v12, v13 and v23
• Three shear moduli are required: G12, G13, G23
• The orientations corresponding to E1 and E2 are specified by XYZ vector components

Duncan-Chang Hyperbolic

The Duncan-Chang Hyperbolic constitutive model [Duncan and Chang, (1970)] is widely used for the modeling of soil behaviour and is capable of modeling the non-linear, stress-dependent and inelastic behaviour of cohesive and cohesionless soils.

The Duncan-Chang Hyperbolic model can only be used in conjunction with the Mohr-Coulomb failure criterion in RS3.

The following input parameters are used to define the Duncan-Chang Hyperbolic model in RS3:

Modulus Number (Ke) - this dimensionless parameter represents Young's Modulus (range of values: 350-1120)

Modulus Exponent (n) - governs the stress dependence of Ke on sigma3 (range of values: 0-1)

Unloading Modulus Number (Ku) - is used to calculate the tangential modulus for unloading/reloading conditions

Failure Ratio (Rf) - defines the shape of the stress-strain curve (range of values: 0.60-0.95)

Atmospheric Pressure (Patm) - used for normalization of stress input

Poisson's Ratio (v) - can be specified as either Constant or Stress Dependent.

• If Poisson's Ratio = Constant, then Poisson's Ratio is entered directly as a constant value.
• If Poisson's Ratio = Stress Dependent, then the Bulk Modulus parameters are entered (see below).

Bulk Modulus Number (Kb) - this dimensionless parameter characterizes the volumetric change (range of values: 200-700)

Bulk Modulus Exponent (m) - governs the stress dependence of Kb on sigma3 (range of values: 0-1)

Based on a hyperbolic stress-strain curve and stress-dependent material properties, the following equations are derived for the Duncan-Chang Hyperbolic model.

The tangential modulus (Et) for a given stress condition, is given by Eqn.1.

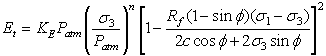
The tangential bulk modulus (Bt) and tangential Poisson's ratio are given by Eqn.2 and Eqn.3 respectively.

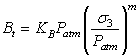
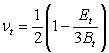
Non-linear Isotropic

A Non-linear Isotropic material has elastic properties that are dependent on some measures of stress or strain tensor. In RS3, there are five (5) possible options for nonlinear elasticity:

• Formula 1, given by Eqn.4
  
  

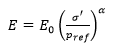
• Formula 2, given by Eqn.5
  

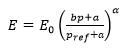
• Formula 3, given by Eqn.6
  

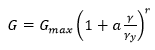
• Formula 4, given by Eqn.7
  

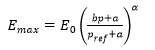
• Formula 5, given by Eqn.8
  

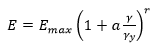
The first two options (Formula 1 and Formula 2) are based on the proportionality between the elastic modulus of porous materials and the confinement.

The third option (Formula 3) is based on laboratory data that suggests degradation of shear modulus with increase in deviatoric strain.

The fourth option (Formula 4) combines the effect of confinement and deviatoric strain to calculate the maximum elastic modulus based on the level of confinement.

The fifth option combines (Formula 5) the effect of confinement and deviatoric strain to calculate the maximum elastic modulus based on the degradation, with deviatoric strain, which depends on the loading history, taken into account.

Custom

A Custom option is provided for the user to enter a custom elastic property model.

Datum Dependent

A Datum Dependent option is provided for the user to enter an elastic property model that is dependent on datum.