Edit Contour Data
The Edit Contour Data dialog contains a variety of options for setting the Contour Type and the method used to compute contours.
To access Edit Contour Data:
- Select Presets > Contour > Edit Contour
 from the Stereonet 2D or Stereonet 3D ribbon.
from the Stereonet 2D or Stereonet 3D ribbon.
Edit Contour Data is also available in the Contours entity's Properties pane.
Contour Data
The data that is contoured on the stereonet is determined by the selection of the Contour Data in the Edit Contour Data dialog. You may select one of the following data types to contour:
The Contour Data can also be selected in the Contour entity's Properties pane.
POLE VECTOR DENSITY
If Pole Vector Density is selected, then the contours will represent either pole or dip vector concentrations, according to the selection of the Pole/Dip Vector Mode.
See the Pole Vector Contour topic for details.
INTERSECTION VECTOR DENSITY
If Intersection Vector Density is selected, then the contours will represent the concentration of intersections. See the Intersection Vector Contour topic for details.
QUANTITATIVE
If the Quantitative option is selected, then you may choose a Quantitative (i.e., numeric) data column from the Pole Data Grid, and the selected data will be contoured on the Stereonet. See the Quantitative Contour topic for details.
Density Calculation
The following options are available, which control the way that DIPS computes the density concentration values for the data:
- Distribution
- Fisher
- Schmidt
- Count Circle Size
The Schmidt distribution method provides very quick computation time and, for large amounts of data, produces concentration values which are very similar to those obtained with the Fisher method. When the quantity of data is limited, however, the Schmidt distribution produces very crude contour diagrams and often misleading results, since each measurement is assumed to be 100 percent accurate and any existing errors are exaggerated due to a lack of data. Therefore, in this case, it is advisable to use the Fisher distribution, since it tends to suppress any undue influence that a single measurement might have on the data contained in a limited data set. When you have lots of data, there is little difference between the plots generated by the two methods, and the Schmidt distribution is faster.
FISHER DISTRIBUTION
In the Fisher method, each pole is assigned a normal influence or Fisher distribution over the surface of the sphere, rather than a point value, as in the Schmidt method. The integrated zone of influence is a bell-shaped distribution with a maximum height of 1, and a basal radius twice that of the counting circle radius. The influence contribution to a grid point is represented by the height of the influence zone immediately above the grid point. In this method, the total influence of an individual pole is the same as in the Schmidt method, but its distribution of influence reflects an assumed probability of measurement error. For large quantities of data, this option will produce similar results to the familiar Schmidt option. The real strength of the Fisher option is in "smoothing" density plots for sparse data sets.
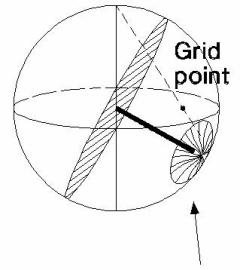
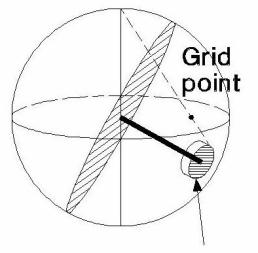
SCHMIDT DISTRIBUTION
The Schmidt distribution is the classical method, in which each pole is assigned a constant influence value of 1. The integrated zone of influence is a cylinder of constant height with a radius equal to the radius of the counting circle. A counting grid is superimposed on the stereonet plane, or in the case of DIPS, on the surface of the reference sphere. Convention dictates the use of a counting circle with an area equivalent to 1% of the lower hemisphere surface. For each pole plotted, any grid point falling within a circle of arbitrary constant radius centered on this pole is incremented by the value of the pole. After the influence of all plotted poles is thus distributed, the density plotted at each grid point is calculated by dividing the pole count at that grid point by the total pole influence.
COUNT CIRCLE
You can customize the Count Circle Size used in the contour calculations.
The generally accepted Count Circle Size used in contour calculations is one percent of the surface area of the lower reference hemisphere. This is, however, merely a convention, and if desired, you may use a different Count Circle Size. The allowed range of the count circle area as a percentage of the hemisphere area is 0.5 % to 5.0 %. For meaningful results, a range limit of 1.0 % to 2.5 % is recommended.
Interpolation
The Interpolation Method option only applies if Contour Data is Qualitative (i.e., you are plotting general data on the stereonet rather than vector densities). The following options are available:
- Inverse Distance
The Inverse Distance interpolation method's "distance" measure is actually an angular difference since we are dealing with orientations.
The Local Cone Angle is set to 90 degrees by default, which means that the interpolation happens over all the data (including wrapping). For localized interpolation, restrict the Local Cone Angle to < 90 degrees.