Wedge Sliding
The Wedge Sliding Kinematic Analysis failure mode is a test for the sliding of wedges formed by the intersection of two planes.
The key elements of Wedge Sliding Kinematic Analysis are:
- Slope plane
- Intersection plotting
- Plane friction cone (angle measured from the perimeter of the stereonet)
Wedges can slide on two planes (along the line of intersection) or on one plane (if one plane has a more favourable orientation for sliding than the line of intersection). Wedge Sliding is based on the analysis of intersections. Dip vectors of individual planes are also considered to determine if wedges slide on two planes or one plane. Pole vectors are not used.
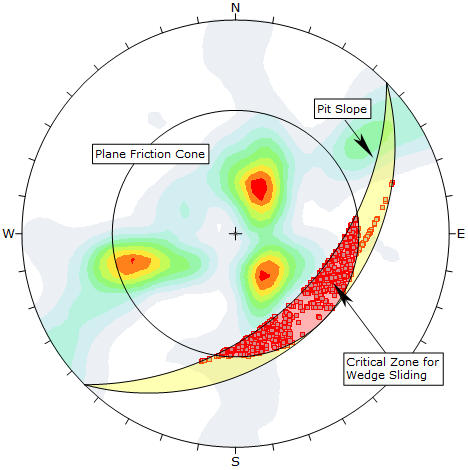
Intersection Plotting
When two joint planes intersect, they can form a wedge which can slide out of the slope (depending on kinematic and frictional considerations). The intersection of two planes forms a line in 3-dimensional space. The trend/plunge of the line plots as a single point on a stereonet, which we refer to as an Intersection.
Wedge Sliding Kinematic Analysis is based on the analysis of intersections. If an intersection point satisfies the frictional and kinematic conditions for sliding, then it represents a risk of Wedge Sliding.
In DIPS, there are several different options for the display of intersections on the stereonet. You can plot:
- Intersection of pole planes in the file (Pole Data Grid planes)
- Contours of all intersections (Pole Data Grid planes)
- Intersections of major planes (i.e., Mean Set Planes and/or User Planes)
In the above figure, the critical intersections of all Pole Data Grid planes are highlighted in the critical zone, and intersection contours are also displayed. Since the maximum contour concentrations do not overlap the critical zone, Wedge Sliding is not likely to be a problem for this example.
See the Intersections Overview topic for more information.
Primary Critical Zone for Wedge Sliding
The primary critical zone for Wedge Sliding is the crescent-shaped area:
- INSIDE the plane friction cone and
- OUTSIDE the slope plane
Intersections that plot in this zone represent wedges which satisfy frictional and kinematic conditions for sliding. This is highlighted in red in the above figure.
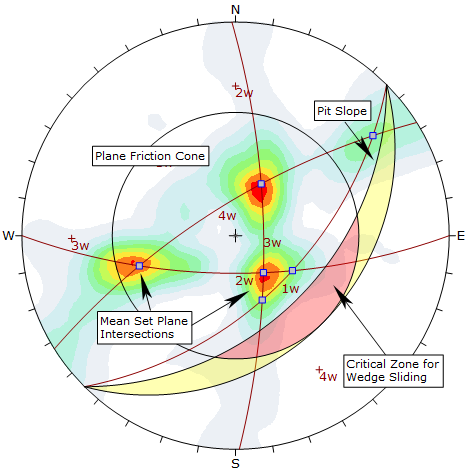
Sliding on Two Planes or One Plane
Depending on the wedge geometry, a wedge may slide along the line of intersection (i.e., on two planes) or on one plane. Sliding on one plane can occur when the dip vector of one of the wedge planes has a more favourable orientation for sliding than the line of intersection.
- In the primary critical zone, wedges can slide on either two planes or one plane.
- In the secondary critical zone, wedges always slide on one plane.
For sliding on a single plane, the dip vector of the sliding plane must be in the primary critical zone. This is the same criterion used for Planar Sliding (with no lateral limits). However, note that critical dip vectors are not displayed on the stereonet for wedge analysis; only the critical intersections are plotted.
Secondary Critical Zone for Wedge Sliding
The secondary critical zone for Wedge Sliding is the area between the slope plane and a plane (great circle) inclined at the friction angle (the two areas highlighted in yellow in the above figure, on either side of the primary critical zone). Critical intersections that plot in these two zones always represent wedges which slide on one joint plane. In this region, the intersections are actually inclined at LESS THAN the friction angle, but sliding can take place on a single joint plane which has a dip vector greater than the friction angle.
Friction Cone
A friction cone defines the limits of frictional stability on a stereonet. For Wedge Sliding analysis, we use a Plane Friction Cone.
When considering intersections (or dip vectors), the friction angle is measured from the EQUATOR (perimeter) of the stereonet. All intersections or dip vectors INSIDE the Plane Friction Cone represent wedges or planes which dip steeper than the friction angle, and can slide if kinematically possible. The cone angle for a Plane Friction Cone = 90° - friction angle.
For Wedge Sliding, it is assumed that both sliding planes have the same friction angle.
Lateral Limits
For Wedge Sliding, we do not consider lateral limits. Since the second joint plane allows an extra degree of freedom of movement, wedges can slide over the entire lateral range. The second joint plane may act as a sliding plane or a release plane.
Wedge Sliding Results
Wedge Sliding analysis results are displayed in the Legend for the currently displayed intersection type (i.e., Pole Planes, Mean Set Planes, User Planes)
- The number of intersections within the critical zone is counted.
- Results are expressed as a percentage of all intersections.
These percentages give an estimate of "feasibility of failure" (not to be mistaken for "probability of failure") with respect to the total number of intersections for the currently displayed Intersection Type.