Equal Area/Equal Angle Projection Method

Equal Area Projection

In the Equal Area method, the bottom of the sphere rests on the projection plane. The point A on the sphere is projected down to the plane by swinging this point in an arc about the contact between the sphere and the plane, giving point B. The resultant projection is then scaled back to the size of the projection sphere.

Equal Angle Projection

For the Equal Angle projection method, a line is drawn from the center of the top of the sphere (the zenith), to a point A on the sphere (a pole or a point on the great circle). The intersection of this line with a horizontal plane through the center of the sphere, defines the projection point B.

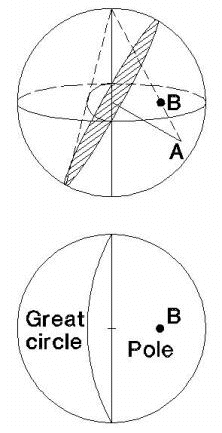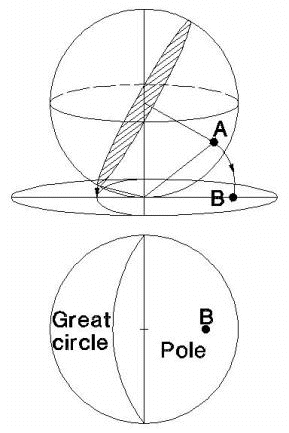Equal Angle Projection Method	Equal Area Projection Method

Equal Angle / Equal Area Comparison

Equal Angle projection preserves the geometry of projected shapes. The area on the surface of the sphere, represented by a projected region, depends on its location. The projected area of a given circle increases towards the equator of the projection (see below for illustration).

Equal Area projection distorts geometrical shapes such as small circles (circles with centers not coincident with that of the sphere). Nevertheless, a constant area on the projection represents a constant area on the surface of the sphere, regardless of its location. This method reduces visual bias in comparisons between data clusters in different parts of the sphere.

EQUAL ANGLE projection	EQUAL AREA projection
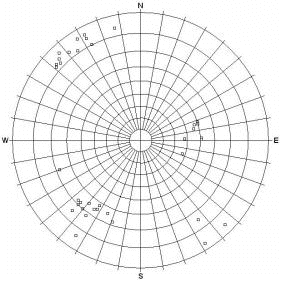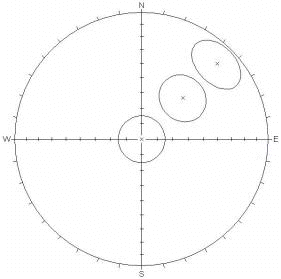
Pole Plot	Pole Plot
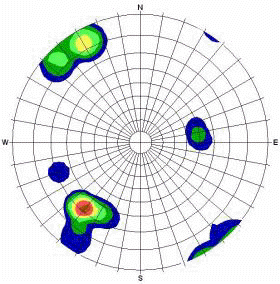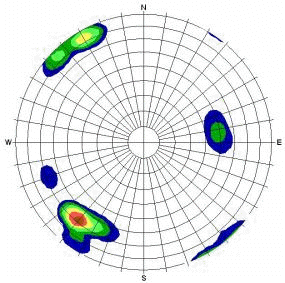Contour Plot	Contour Plot
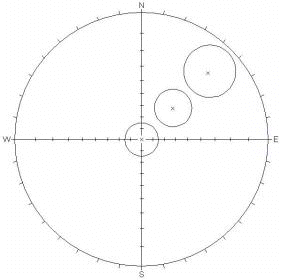Small Circles, 15 ° cone angle (circles remain circular, but increase in area towards the equator)	Small Circles, 15 ° cone angle (circles have equal area, but become elliptical towards equator)

The choice of projection ( Equal Angle or Equal Area) has no effect on the calculated mean plane for sets. The mean plane calculations are done using the raw data on the reference sphere. The projection type affects the display of the 2-dimensional Stereonet, but does not affect the calculation of the mean plane of a joint set.

If you switch between Equal Angle and Equal Area, using the same Set Windows, you should get identical results for the Mean Set Planes.

Equal Angle vs Equal Area

When making visual estimates of clusters and variabilities, it is actually more appropriate to use Equal Area projection to reduce areal distortion and improve visual estimates.

Since using Equal Area preserves areas (i.e., relative areas on reference sphere versus projection), this means that there is no distortion of area from the center of the stereonet to the perimeter, therefore allowing you to more accurately compare sets anywhere on the projection. So you might consider Equal Area to be more suitable when you are initially determining the extent of sets and their relative importance. Of course, the Fisher concentration also determine the ranking of sets.

If you are performing Kinematic Analysis, then Equal Angle projection is more appropriate. Since angular relationships and shapes are preserved (e.g., small circles remain circular anywhere on the stereonet), you can more accurately assess kinematic stability with an Equal Angle projection.

In general, the relevance of Equal Angle versus Equal Area was probably a more important issue in the days of manual stereonets, when it took a great deal of time to generate even the most basic plots. Furthermore, since detailed post-processing (e.g., wedge stability analysis with factor of safety) is now handled by other software packages (such as RocSlope2 and UnWedge) the issue of stereonet projection is of even less importance.