Flexural Toppling

The Flexural Toppling Kinematic Analysis failure mode is a test for Flexural Toppling as defined in Goodman (1980).

The key elements of Flexural Toppling Kinematic Analysis are:

• Slope plane
• Slip limit plane (based on slope angle and friction angle)
• Lateral limits

For Flexural Toppling, you can use either Pole Vector Mode or Dip Vector Mode. The results are equivalent regardless of the vector mode.

Pole Vector Mode

To carry out Flexural Toppling analysis using pole vectors, the Pole Vector Mode must be in effect.

• Select Vector Mode > Pole Vector from the Stereonet 2D ribbon.

For Flexural Toppling using pole vectors, the critical zone for toppling is defined by the region:

• OUTSIDE the slip limit plane (see below for the definition of the slip limit plane)
• INSIDE the lateral limits

All poles that plot in this region represent a toppling risk. This is illustrated in the figure below.

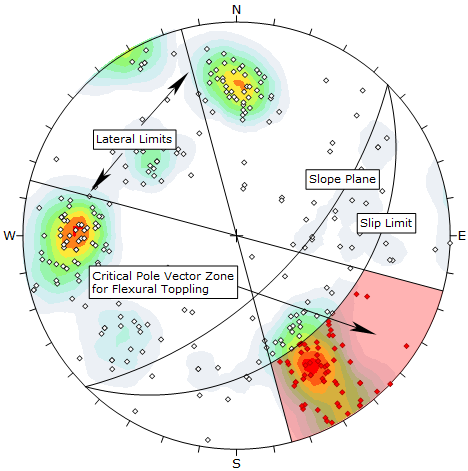
In this example, the friction angle = 30°, slope dip = 60°, slope dip direction = 135°, lateral limits = 30° (plus/minus).

Dip Vector Mode

To carry out Flexural Toppling analysis using dip vectors, the Dip Vector Mode must be in effect.

• Select Vector Mode > Dip Vector from the Stereonet 2D ribbon.

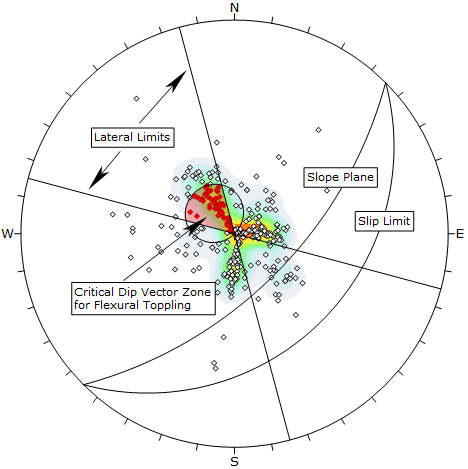
For Flexural Toppling using dip vectors, the critical zone for toppling is defined by the region:

• INSIDE the daylight envelope of the slip limit plane (see below for the definition of the slip limit plane)
• INSIDE the lateral limits

All dip vectors that plot in this region represent a toppling risk. This is illustrated in the figure below. The input is the same as the pole vector example above.

NOTES:

The slip limit plane is not an actual physical plane although it is derived from the slope angle and friction angle. Furthermore, the daylight envelope of the slip limit plane is also not a physical construct, however it serves the purpose of defining a critical toppling zone for dip vectors.

Although the critical toppling region for dip vectors may appear to be much smaller than the equivalent toppling region for pole vectors, they do in fact represent the same critical zones. Also, remember that the Projection Type changes the apparent areas on the stereonet. In these figures, we have used Equal Angle projection. If you use the Equal Area projection, the pole and dip vector critical zones will be closer in apparent size, although the dip vector region will still appear smaller due to the inherent nature of the Flexural Toppling analysis.

Slip Limit

Planes cannot topple if they cannot slide with respect to one another. Goodman (1980) states that for slip to occur, the bedding normal must be inclined less steeply than a line inclined at an angle equivalent to the friction angle above the slope.

This results in a “slip limit” plane, which defines the critical zone for Flexural Toppling. The dip angle of the slip limit plane is derived from the Slope Dip – Friction Angle (in this example 60° – 30° = 30°). The Dip Direction of the slip limit plane is equal to that of the slope face.

Lateral Limits

The Lateral Limits for Flexural Toppling have the same purpose as described for Planar Sliding. They define the lateral extents of the critical zone with respect to the dip direction of the slope. See the Planar Sliding topic for more information.

Flexural Toppling Results

Flexural Toppling results are displayed in the Legend.

• The number of poles (or dip vectors) within the critical zone are counted.
• Results are expressed as a percentage of all poles in the file, and as a percentage of poles within individual Sets (if sets are defined).

These percentages give an estimate of "feasibility of failure" (not to be mistaken for "probability of failure") with respect to all planes in the file, and with respect to all planes in individual sets. It does not matter whether you are viewing poles or dip vectors; the results are identical since the critical zones are equivalent for pole or dip vectors.