Optimize Surfaces
The Optimize Surfaces option is available in the Surface Options dialog if Surface Type = Non-Circular.
The Optimize Surfaces option is a very powerful search technique, which allows you to search for lower safety factor slip surfaces, using the surfaces generated by a non-circular search or specific user-defined slip surfaces, as a starting point.
To enable the Optimize Surfaces option:
- Select the Optimize Surfaces checkbox in the Surface Options dialog.
- Various analysis options are available by selecting the Settings button beside the Optimize Surfaces checkbox. See below for details.
There are two optimization techniques available in Slide2: Monte Carlo and Surface Altering. Surface Altering is recommended - it is faster than Monte Carlo and able to find more critical surfaces.
Optimization Search: Monte Carlo
The Optimize Surfaces option is based on a Monte Carlo technique, often referred to as "random walking". For a detailed description of the algorithm, refer to Greco, 1996.
When used in conjunction with a non-circular search (e.g. Block Search or Path Search) the Optimize Surfaces option can be very effective at locating slip surfaces with lower safety factors.
Although the option is referred to as "optimization" in Slide2, it can also be considered an additional Search Method. It does not require that a non-circular search be carried out. It can be used as an independent search method, starting with only a single, user-defined non-circular slip surface, as a starting point for the optimization search.
A simplified description of the algorithm follows:
- The factor of safety is calculated for the initial slip surface.
- The location of one vertex on the surface is randomly modified.
- The factor of safety is calculated for the new surface.
- If the factor of safety for the modified surface is lower than the factor of safety for the initial surface, the new surface replaces the original surface, and the location of another vertex is modified. The process is then repeated.
- If the factor of safety for the modified surface is higher than the factor of safety for the initial surface (or the change in the factor of safety is lower than some tolerance) the process ends.
This technique is known as "random walking", since a randomly generated number determines the direction that the vertices are moved. There is no complex underlying algorithm that is searching for the surface. The only data that is used to determine whether one surface is preferable to another, is the factor of safety.
As with many other optimization techniques, this method will become "trapped" in a local minimum, and is not guaranteed to find a global minimum for the factor of safety. However, notwithstanding the simplicity of the algorithm, the results typically compare very well with more complex methods of searching for global minimums (e.g. simplex, conjugate-gradient, etc).
The best application of random walking optimization is to use it to optimize a surface that is already considered to be a good surface (i.e. already close to a local or global minimum, for example, determined by a non-circular search). Try the Optimize Surfaces option, using the Global Minimum as the initial surface, and see how Optimize Surfaces determines the optimum location where the surface exits the weak layer.
A similar optimization algorithm is also described inf.
Optimization Search: Surface Altering
The Surface Altering Optimization (SA) option is a local search method which uses the results of the primary search method (e.g. Cuckoo search).
SA is a powerful tool to yield lower factors of safety by modifying geometry of a given slip surface. SA is a novel approach based on a derivative-free constrained nonlinear optimization*.
Unlike the metaheuristic method, SA is a local optimization method.
- The optimization process is stopped when either the maximum number of iterations is reached or when the optimization does not make any further progress.
*Bound Optimization BY Quadratic Approximations (BOBYQA) developed by Powell in 2009.
For additional information about Surface Altering Optimization, please refer to this document.
Surface Optimization Settings
There are several options and settings associated with the Optimize Surfaces option, which may be customized by the user. They are available by selecting the Settings button beside the Optimize Surfaces checkbox in the Surface Options dialog. This will display the Optimize Surfaces Settings dialog, in which the following options are available.
Surfaces to Optimize
- Global Minimum – in most cases, you will probably wish to use the Global Minimum surface determined from the search as a starting point for the Optimize Surfaces option.
- All – this option will perform the optimization on EVERY SURFACE generated by the search. If you choose this option, the analysis may take a noticeably longer time to complete.
- Factor of Safety Less Than – this option will perform the optimization on all surfaces with a factor of safety less than the specified value. This allows you to "filter out" high safety factor surfaces, which are probably not a good starting point for the optimization.
Optimization Options
- Tolerance – The convergence criterion for the optimization. When the difference in safety factor between the current iteration, and the average safety factor of the last five iterations (including the current iteration), is less than the Tolerance, then the optimization is considered to have converged and the calculation is ended.
- Maximum Number of Iterations – the number of iterations allowed for the optimization. If this number is reached, then the optimization is automatically terminated, and the results at the final iteration are reported.
- Step Reduction Factor – this number is a factor (0 to 1) which determines the relative distance by which vertices are moved, during each iteration of the optimization. A small value may lead to long computational time, while a high value may lead to a premature termination of the iteration process. The default value of 0.5 is recommended.
- Explore All Vertices Before Moving Surface – if this checkbox is selected, then the optimal direction of movement will be determined for each vertex, and all vertices will be moved at once. If this checkbox is NOT selected, then the optimal direction of movement is determined for a vertex, the vertex is moved, and the process is repeated on the next vertex.
- Maximum Concave Angle - If this checkbox is selected you can define the maximum allowable concave angle between adjacent segments of a slip surface. If this checkbox is not selected, then concave angles will not be allowed for slip surfaces generated by the optimization search.
Snap Shallow Surfaces to Slope
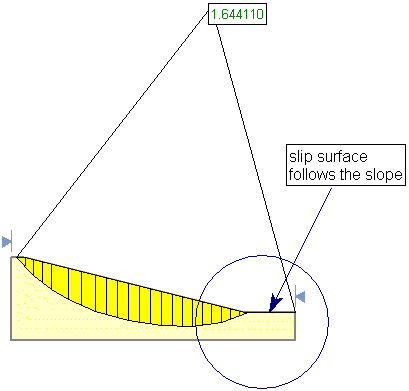
In certain cases, the Optimization algorithm may generate a slip surface which "follows" the slope surface, at a very shallow depth beneath the surface. This usually occurs at either end of the slip surface, as illustrated in the following figure.
Very shallow slip surface at toe of slope
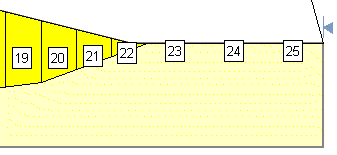
In the above example, very shallow slices have been created at the toe of the slope. You may not be able to see them without zooming in, however, if you turn on the slice numbers in Display Options, you can see the location of the slices. This is illustrated below.
Slice numbers displayed, indicating the location of shallow slices at toe of slope.
A slip surface such as this is clearly not kinematically feasible, and the calculated safety factor may be incorrect (usually too low). If you ever see results similar to this, after using the Optimization option, then you should select the Snap Shallow Surfaces to Slope checkbox and re-run the analysis. This will automatically "remove" very shallow portions at the ends of the slip surface, and the safety factor will be re-calculated for the slip surface.
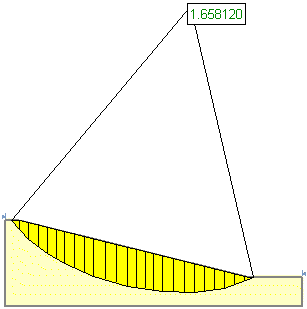
For this example, if the analysis is re-run using the Snap Shallow Surfaces to Slope option, the resulting slip surface and safety factor are shown below. Notice that the safety factor is noticeably larger after re-running the analysis (1.658 vs. 1.644).
Analysis re-run using the Snap Shallow Surfaces to Slope option
Specify Distance
If you are using the Snap Shallow Surfaces to Slope option, then you may also specify the minimum distance allowed between the slip surface and the slope.
- If the Specify Distance checkbox is NOT selected, then the program will automatically determine a minimum allowable depth for the slip surface. If any vertex of the slip surface is within this distance of the slope surface, then the vertex will automatically be snapped up to the slope.
- If the Specify Distance checkbox is selected then you can specify the minimum allowable distance.
Use checks for depth, elevation, concave surfaces
This checkbox refers to the options in the Surface Options dialog. If this checkbox is selected in the Optimize Surfaces dialog, then the optimization search will use the settings for:
- Minimum Elevation
- Minimum Depth
- Concave Surfaces
as specified in the Surface Options dialog (if applicable) for the search method.