Snowden Modified Anisotropic Linear

The Snowden Modified Anisotropic Linear strength model is based on the Anisotropic Linear strength model, with the following additional properties (Mercer, 2012; Mercer, 2013):

• Allows you to define non-linear stress-dependent strength envelopes for the rock mass and bedding material, and
• Allows non-symmetric anisotropy.

For a general background read the Anisotropic Linear strength topic. The differences between the Anisotropic Linear and Snowden Modified Anisotropic Linear models are discussed below.

Non-symmetric Anisotropy

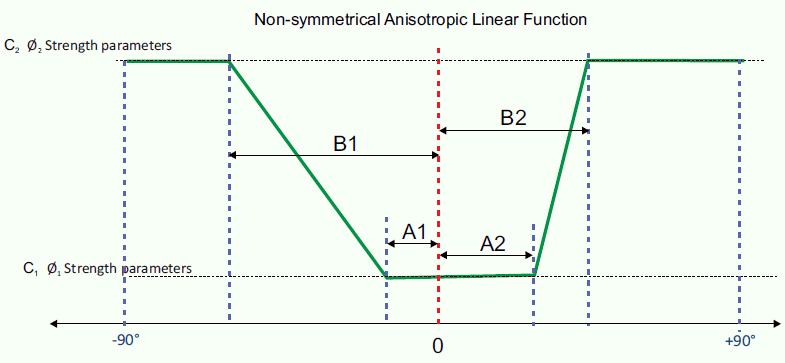
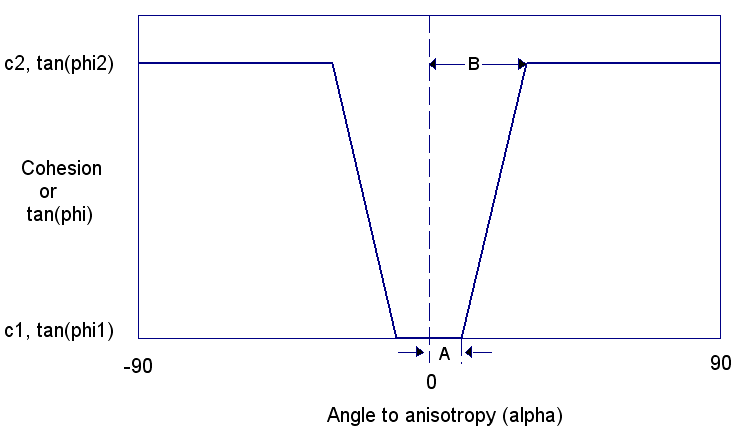
The Snowden Modified Anisotropic Linear model allows you to define a non-symmetric anisotropy function as shown below, using four parameters A1, A2, B1 and B2. Compare this with the symmetric function for the Anisotropic Linear model in the next figure which only uses two variables A and B.

Both the Snowden Modified Anisotropic Linear model and the Anisotropic Linear model assume a linear transition between the bedding plane strength and the rock mass strength.

Strength Functions for Rock Mass and Bedding

The original Anisotropic Linear model assumes constant values of cohesion and friction angle for the bedding and rock mass. For the Snowden Modified Anisotropic Linear model, you can define non-linear strength functions for the bedding and rock mass, as follows:

1. Select the Bedding Strength Function button in the Define Material Properties dialog.
2. You will see the Define Bedding Strength Function dialog.
3. You can define a strength function in one of two ways:
• Shear-Normal function
• Cohesion-Friction function

By default, you can define a Shear-Normal strength function by entering Normal and Shear stress data in the grid. Alternatively, you can select the Cohesion-Friction function option, and enter Normal stress, cohesion and friction data in the grid. You can also import strength functions by selecting the Import button.

1. When you have finished entering the data select OK to save the function and return to the Define Material Properties dialog.
2. Select the Rock Mass Strength Function button in the Define Material Properties dialog.
3. You will see the Define Rock Mass Strength Function dialog.
4. Repeat steps 3 and 4 to define a strength function for the rock mass.

Slide2 will use the Bedding Strength function, the Rock Mass Strength function and the Anisotropy function (first figure above) to determine the stress-dependent shear strength for any shear plane. For any shear plane (i.e. slice base) at any orientation:

• The Bedding Strength Function defines the strength within the angular range between A1 and A2 in the top figure.
• The Rock Mass Strength Function defines the strength for angles outside of the range defined by B1 and B2 in the top figure.
• For intermediate orientations, both bedding and rock mass strength functions are computed, and the final shear strength is a weighted average determined by the linear transition of the anisotropy function.

Suggested Method of Obtaining Strength Functions

Shear-normal strength functions for the rock mass and bedding may not always be readily available. One possible method of obtaining these functions is to use the Rocscience program RSData to convert other strength criteria envelopes (e.g. Generalized Hoek-Brown and Barton-Bandis) into shear-normal functions as follows:

1. In RSData program, enter the rock mass strength parameters using the Generalized Hoek-Brown criterion. For the Failure Envelope Range, choose Custom Application and a value of sig3max for your slope. The resulting shear stress versus normal stress envelope should cover the range of effective normal stresses you anticipate on all possible failure surfaces.
2. In the File > Export menu, select the Slide2 Shear/Normal Function option and save the rock mass shear-normal function.
3. Define the bedding strength using the Barton-Bandis strength criterion and repeat steps 1 and 2 to obtain a shear-normal strength function for the bedding.
4. Import the shear-normal functions into Slide2 using the Import option for the Snowden Modified Anisotropic strength functions for rock mass and bedding.

Anisotropy Definition

For the Snowden Modified Anisotropic Linear strength model there are two methods of defining the direction of the anisotropy:

• Angle
• Surface

If the Anisotropy Definition = Angle then the direction of anisotropy is constant and defined by a single angle which is entered in the Angle (ccw to 1) edit box. The definition of the angle is illustrated in the Anisotropic Linear topic.

If the Anisotropy Definition = Surface then the direction of anisotropy can be variable and defined by an Anisotropic Surface. Select the desired anisotropic surface from the Anisotropic Surface list box.

Anisotropic Surface

If you have chosen Anisotropy Definition = Surface, then you must select a surface from the Anisotropic Surface list box. If the list box is disabled, this means that you have not defined any anisotropic surfaces. You must use the Add Anisotropic Surface option to define an anisotropic surface. See the Anisotropic Surface Overview topic for more information.