Using Response Surface

Although many verification examples have proven it to agree well with Latin-Hypercube results, it cannot always guarantee a result that is identical. However, it will be able to give you a ballpark PF value. It is always recommended to run at least one Latin-Hypercube Overall Slope analysis overnight.

A probabilistic analysis with response surface is set up in the same way as any other probabilistic analysis:

Important Notes:

• Response Surface cannot be used in conjunction with a beta distributed input variable.
• The required initial computations used by response surface are a function of the number of random variables defined in the model. If the user's defined number of samples is smaller than the number of samples needed by Response Surface, the user's number of samples is computed with Latin-Hybercube only.
• After a Response Surface Overall Slope computation, the “Show All Surfaces” button will only show the surfaces for the samples that were computed in order to train the model.

Stochastic Response Surface Theory

How it works:

1. Convert all random variables to standard normal random variables, N(0,1).

2. Represent resulting FS in polynomial chaos expansion form. In Slide2, a 3^rd order Hermite expansion is used.

3. Use a small number of computations to determine the coefficients of the polynomial in Step 2.

4. Generate Latin-Hypercube samples and plug them into the polynomial to estimate FS.

STEP 1

The initial random variables are converted to standard normal random variables using transformation equations (Li et al., 2011).

STEP 2

The Hermite polynomial expansion looks like this:

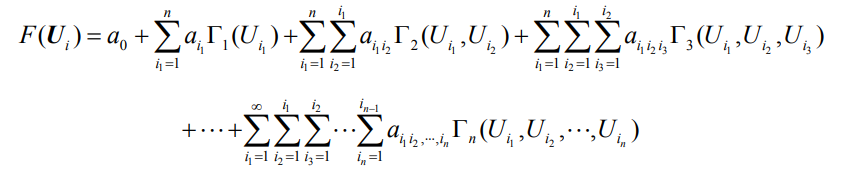
In the above, F is the factor of safety and U_i is the particular combination of standard normal random variables in a simulation. The coefficients a must be determined.

In Slide2, a 3^rd order Hermite expansion is used.

STEP 3

Let n=number of random variables defined, and N = number of computations required. The number of computations required is determined as follows:

If 1 random variable is defined (n=1), N=15 simulations are computed.

If n random variables are defined, the number of simulations computed (N) is:

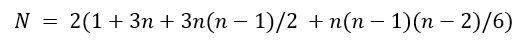
If the N determined from the equation above is larger than the number of samples (S) defined by the user in the Statistics section of the Project Settings dialog, then only the user-defined number of samples are computed using the Latin-Hypercube sampling method.

These N computations are generated using Latin-Hypercube sampling (Choi et al., 2004) to ensure that the solution space is well-covered. They are then used to determine the polynomial coefficients associated with each variable or variable combination.

STEP 4

The number of samples defined by the user (S) in the Statistics section of the Project Settings dialog, is generated using Latin-Hypercube sampling method. The samples are matched with the corresponding coefficients and the resulting FS is predicted. The PF is estimated from these predicted FS values.

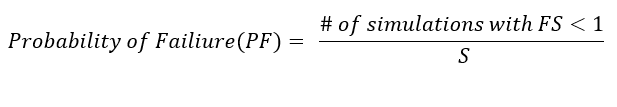
References for response surface:

Choi, S. K., Grandhi, R. V., Canfield, R. A., & Pettit, C. L. (2004). Polynomial chaos expansion with latin hypercube sampling for estimating response variability. AIAA Journal, 42(6), 1191-1198.

Isukapalli, S. S. (1999). Uncertainty analysis of transport-transformation models.

Li, D., Chen, Y., Lu, W., & Zhou, C. (2011). Stochastic response surface method for reliability analysis of rock slopes involving correlated non-normal variables. Computers and Geotechnics, 38(1), 58-68.