Probabilistic Results Overview

If your Slide2 analysis includes either a Probabilistic Analysis or a Sensitivity Analysis, then the Probabilistic and/or Sensitivity analysis results, are viewed using the options in the Statistics menu in the Slide2 Interpret program.

• After a Probabilistic Analysis, you can view Histogram, Cumulative, Scatter or Convergence Plots.
• After a Sensitivity Analysis, you can view a Sensitivity Plot.

Of primary interest after a Probabilistic Analysis, are the Probability of Failure, and the Reliability Index for the slope. These are discussed below.

Probability of Failure

After a Probabilistic Analysis, the Probability of Failure (PF = ##) for the Global Minimum slip surface, is displayed as shown in the following figure.

Display of Probability of Failure

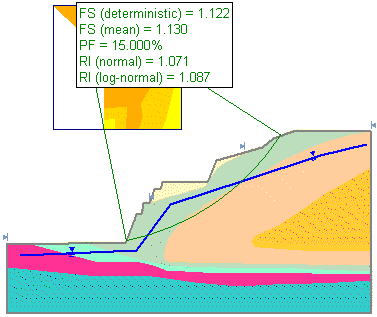
The definition of Probability of Failure in Slide2, is simply:

where:

• numfailed = Number of Analyses with Safety Factor < 1
• numtotal = Total number of analyses (samples)

If all sample iterations of the Probabilistic Analysis yielded a valid result (safety factor), then numtotal = Number of Samples. If the safety factor could not be calculated for some analyses, then numtotal = total number of VALID analyses. For example, if Number of Samples = 1000, and a valid safety factor could not be calculated for 10 samples, then the actual numtotal = ( 1000 – 10) = 990, will be used to calculate the Probability of Failure.

Reliability Index

Another commonly used measure of safety, after a Probabilistic Analysis, is the Reliability Index. The Reliability Index (RI = ###) is displayed in the Legend as shown in the previous figure. The Reliability Index is defined as follows.

If one assumes that the distribution of safety factors, after a probabilistic analysis, is NORMALLY distributed, then the following equation is used to calculate the Reliability Index:

Eqn. 1

where:

b = Reliability Index,

m = Mean Factor of Safety,

s = Standard Deviation of FS

As can be seen from Equation 1, the Reliability Index represents the number of standard deviations which separate the MEAN Factor of Safety, from the critical Factor of Safety ( = 1 ).

• As a rule of thumb, the Reliability Index should be at least 3 or greater, to have reasonable assurance of a safe slope design.
• A Reliability Index = 0, implies that the Mean Factor of Safety = 1.
• A negative Reliability Index indicates a Mean Factor of Safety less than 1.

If one assumes that the distribution of safety factors, after a probabilistic analysis, is LOGNORMALLY distributed, then the following equation is used to calculate the Reliability Index:

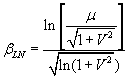Eqn. 2

where:

= lognormal Reliability Index

m = Mean Factor of Safety

V = coefficient of variation of Factor of Safety = s / m

s = Standard Deviation of FS

In reality, the Factor of Safety distribution is often best fit by a Lognormal rather than a Normal distribution, and therefore Equation 2 is frequently used to calculate the (lognormal) Reliability Index. Remember that the Lognormal distribution is only applicable for variables which are always greater than zero, which is the case for Factor of Safety.

The Reliability Index information can be found in the following locations in the Slide2 Interpret program:

• In the Report Generator, the Reliability Index is always reported for BOTH the Normal (Equation 1) and Lognormal (Equation 2) assumptions. Also, the best fit PDF for the Factor of Safety distribution is listed.
• On the main model view, the Reliability Index ( RI = ### ) is listed beside the slip center for the Global Minimum slip surface.
• On Histogram Plots of Factor of Safety, the Reliability Index is listed at the bottom of the plot.

• If the best fit distribution = Lognormal, then the Lognormal Reliability Index (Equation 2) is listed.
• If the best fit distribution = Normal (or any other distribution except Lognormal), then the Normal Reliability Index (Equation 1) is listed.

Probabilistic Analysis Type

In Slide2 there are two different types of Probabilistic Analysis which can be carried out:

• The Global Minimum Method
• The Overall Slope Method

The Probabilistic Analysis Type is selected in Project Settings in the Slide2 Model program. When you are interpreting the results of the probabilistic analysis, you should keep in mind how each analysis is carried out.

Probabilistic Analysis Type = Global Minimum

If the Probabilistic Analysis Type = Global Minimum, then the Probabilistic Analysis is only carried out on the deterministic Global Minimum slip surface. Therefore the probability of failure and reliability index for the slope are only based on the analysis of one slip surface – the deterministic Global Minimum slip surface (also referred to as the Critical Deterministic Surface).

Probabilistic Analysis Type = Overall Slope

If the Probabilistic Analysis Type = Overall Slope, the definitions of Probability of Failure and Reliability Index, are the same as described above. However, you must keep in mind how this type of analysis is carried out.

• For the Overall Slope method, the entire slip surface search is repeated N times, where N = Number of Samples. In this case, EACH ITERATION of the Probabilistic Analysis, can locate a different Global Minimum slip surface. In general, several different Global Minimum slip surfaces will be located by this method (for example, 10 to 50 different Global Minimum surfaces, can be typical).
• The display of these Global Minimum slip surfaces can be toggled ON or OFF with the Show GM Surfaces option in the Statistics menu (by default the display is ON when you open a file).
• The safety factors used to calculate the Probability of Failure and the Reliability Index, are obtained from ALL of the different Global Minimum slip surfaces, displayed by the Show GM Surfaces option, and NOT just the Deterministic Global Minimum slip surface.

The Probability of Failure ( PF = ### ) and Reliability Index ( RI = ### ) for the Overall Slope results are displayed in the Legend.

If you wish to view results for a selected subset of these Global Minimum slip surfaces, then surfaces can be selected with the Pick GM Surfaces option in the Statistics menu. After surfaces have been selected, then the data for the selected surfaces can be viewed using the Highlight Data option for Histogram or Scatter plots.

For more information, see the Show GM Surfaces and Pick GM Surfaces topics.

Critical Probabilistic Surface

If the Probabilistic Analysis Type = Overall Slope, then the Critical Probabilistic slip surface can also be displayed. This is the slip surface, of all slip surfaces analyzed, which has the Minimum Reliability Index. By definition, this slip surface also has the Maximum Probability of Failure. The Critical Probabilistic Surface WILL NOT NECESSARILY BE THE SAME AS THE CRITICAL DETERMINISTIC SLIP SURFACE (i.e. the Global Minimum slip surface – the slip surface with the lowest safety factor when all input parameters are equal to their mean value).

Also, the RI of the Critical Probabilistic Surface, will (in general), NOT be equal to the RI which is obtained using the aggregate safety factor data of all of the different Global Minimum slip surfaces which are located by the Overall Slope analysis.

• The RI of the Critical Probabilistic Surface will always be GREATER THAN the RI for the entire analysis (i.e. the RI displayed in the Legend).
• The PF of the Critical Probabilistic Surface will always be LESS THAN the PF for the entire analysis (i.e. the PF displayed in the Legend).

The Critical Probabilistic Surface, therefore, provides a less conservative measure of the probabilistic slope stability, compared to the results reported using ALL Global Minimum surfaces located by the Overall Slope analysis.

For more information, see the Critical Probabilistic Surface topic.