Water Table Statistics

The method of defining the Water Table location as a Random Variable is a little different than the method used for most other Random Variables in Slide2.

• The Minimum and Maximum locations of the Water Table are specified graphically, by drawing the location of the limiting boundaries on the model.
• The statistical distribution of the Water Table location is specified by defining a Normalized Random Variable with a range of 0 to 1. ZERO represents the location of the Minimum Water Table boundary, ONE represents the location of the Maximum Water Table boundary. The distribution of the Random Variable between 0 and 1, specifies the distribution of the Water Table elevation, between the Minimum and the Maximum Water Table boundaries.

Probabilistic Water Table Boundaries

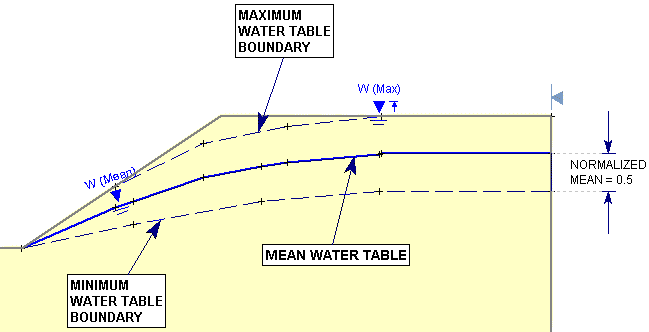
Overview of Probabilistic Water Table

The general procedure for defining the Water Table as a Random Variable in Slide2, is as follows.

1. A random Water Table in Slide2 requires THREE boundaries:
• Maximum Water Table
• Mean Water Table
• Minimum Water Table
2. If your model already includes a Deterministic Water Table (i.e. a Water Table created with the Add Water Table option in the Boundaries menu), then you can specify that the Deterministic Water Table is used as the Mean, Minimum or Maximum water table boundary, for the Probabilistic Analysis (select Statistics > Water Table > Statistical Properties).
3. Depending on your selection in Step 2 (if applicable), you must then draw the Minimum and/or Maximum Water Table boundaries (select Statistics > Water Table > Draw Max Water Table or Draw Min Water Table).
4. After the first two boundaries are defined, the THIRD boundary is then automatically calculated.
5. Now select Statistics > Water Table > Statistical Properties, and define the Statistical Distribution of the Water Table location. This is done in terms of NORMALIZED mean and standard deviation values, where the Normalized parameters define the distribution of the water table elevation, along any vertical line between the Minimum and Maximum Water Table boundaries.

Further information about these options is described below.

Use Deterministic Water Table

If your model already includes a Water Table (i.e. a Water Table created with the Add Water Table option in the Boundaries menu), then it is likely that you will want to use this Water Table (referred to as the Deterministic Water Table), as a Water Table boundary in your Probabilistic Analysis.

For this purpose, the Use Deterministic Water Table As option is available, in the Water Table Statistics dialog (select Statistics > Water Table > Statistical Properties). With this option, you may specify that the Deterministic Water Table, is to be used as the Mean, Minimum or Maximum Water Table boundary, in the Probabilistic Analysis. Or you may specify that it is Not Used. Depending on the setting of this option, you will have to draw the Minimum and/or Maximum Water Table boundaries. The third boundary is then automatically calculated. The four different possibilities are summarized below.

Four possibilities for creating Probabilistic Water Table boundaries

Automatic Calculation of Mean or Minimum Water Table

Depending on the setting of the Use Deterministic Water Table option in the Water Table Statistics dialog, there are two possibilities for the automatic calculation of the THIRD Water Table boundary.

1. The MEAN Water Table can be automatically calculated from the MINIMUM and MAXIMUM Water Table boundaries. OR
2. The MINIMUM Water Table can be automatically calculated from the MEAN and MAXIMUM Water Table boundaries.

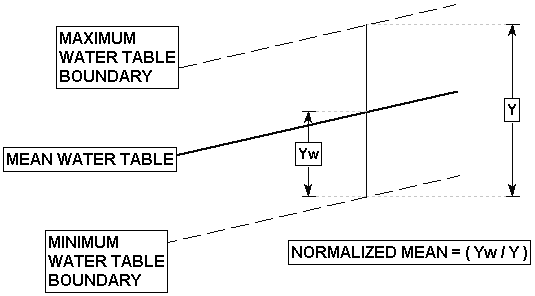
In either case, the location of the CALCULATED Water Table, is determined by the value of the Normalized Mean in the Water Table Statistics dialog. The Normalized Mean is the relative elevation of the Mean Water Table, along any vertical line between the Minimum and Maximum water table boundaries. By default, the Normalized Mean = 0.5, so that the calculated Water Table boundary will be positioned such that the MEAN Water Table is located exactly midway BETWEEN the Minimum and Maximum Water Table boundaries.

No Deterministic Water Table

If your model has NO Deterministic Water Table defined, and you wish to proceed directly to a Probabilistic Analysis using a Water Table, then BOTH the Minimum and Maximum Water Table boundaries will have to be drawn, and the Mean Water Table will be automatically calculated.

Creating Water Table Boundaries

1. To define a Maximum Water Table boundary, select Statistics > Water Table > Draw Max Water Table.
2. To define a Minimum Water Table boundary, select Statistics > Water Table > Draw M in Water Table.
3. The method of defining the Minimum or Maximum water table boundaries, is the same as other boundaries in Slide2. You may draw the boundaries graphically and/or use keyboard entry to define the boundary vertices. For example, see the Add Water Table topic for details.
4. There are no restrictions on the locations of these boundaries, except that the Minimum boundary must be located BELOW (or equal to) the Maximum boundary, at all locations. The Minimum and Maximum boundaries can overlap, if necessary, but they cannot cross each other.
5. The Minimum and Maximum water table boundaries should have the same lateral extents (i.e. left and right X coordinates).

Editing Water Table Boundaries

If you need to edit the Water Table boundaries, remember the following:

1. The water table boundaries which you have drawn, can be moved, edited and deleted like any other boundary in Slide2.
2. However, the CALCULATED Water Table boundary CANNOT be edited directly. That is, you cannot move or delete vertices, or move the boundary.

EXAMPLE: If you have drawn the Minimum and Maximum Water Table boundaries, then you will NOT be able to edit the Mean Water Table.

3. The position of the CALCULATED boundary can only be changed, by changing the value of the Normalized Mean, or by editing the other two water table boundaries.

Water Table Statistics

After the probabilistic Water Table boundaries have been defined, you must define the statistical distribution of the water table location between the Minimum and Maximum boundaries. The Statistical Distribution, Normalized Mean and Normalized Standard Deviation, are specified in the Water Table Statistics dialog.

• You can access this dialog by selecting Statistics > Water Table > Statistical Properties.
• Or a convenient right-click shortcut is also available – simply RIGHT CLICK the mouse anywhere on the Minimum, Mean or Maximum Water Table boundaries, and select Statistical Properties from the popup menu which will appear.

The statistical parameters which define the Water Table location are described below.

Normalized Mean

The definition of the Normalized Mean water table location, is illustrated in the following figure. The Normalized Mean is simply the relative elevation of the Mean Water Table, along any vertical line between the Minimum and Maximum water table boundaries.

Definition of Normalized Mean Water Table Location

The Normalized Mean must have a value between 0 and 1.

• The default Normalized Mean (= 0.5) produces a Mean Water Table which is exactly midway between the Minimum and Maximum boundaries, at all locations.
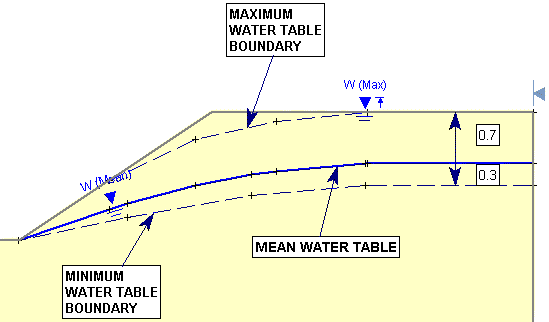
• As another example, if the Normalized Mean = 0.3, the Mean Water Table would be located as shown in the following figure.

Normalized Mean = 0.3

Mean Water Table

The significance of the Mean Water Table boundary is the following.

1. The Mean Water Table is used in the regular (DETERMINISTIC, safety factor) slope stability analysis. Remember that the regular (DETERMINISTIC, safety factor) analysis is always performed before the Probabilistic slope stability analysis when you select Compute.
If you have specified the original (deterministic) Water Table as either the Maximum or the Minimum Water Table for the Probabilistic Analysis, then the deterministic analysis will use the MEAN water table, and NOT the original deterministic Water Table.
2. The Mean Water Table also represents the statistical mean location, of the distribution of random water tables generated during the Probabilistic Analysis.

Statistical Distribution

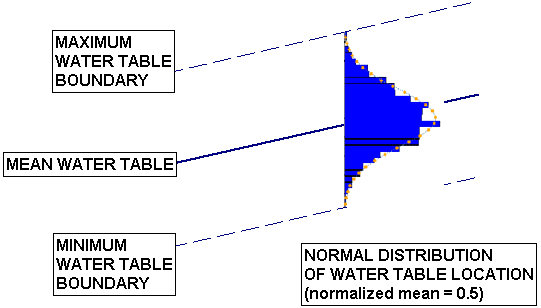
Like other Random Variables in Slide2, a Statistical Distribution must be selected for the Water Table location. By default, a Normal Distribution is specified.

Normal Distribution of Water Table Location

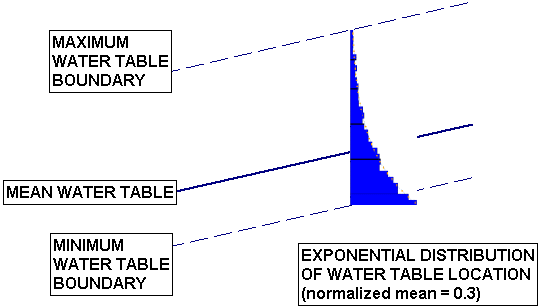
For the Water Table location, it is worth noting that an Exponential Distribution may also be useful. An Exponential Distribution can be used to simulate the occurrence of infrequent heavy rainfall (i.e. the majority of samples would be generated closer to the Minimum Water Table location, and the Maximum Water Table location would only have a small probability of occurring). If you are using an Exponential Distribution, you may want to set the Normalized Mean to a lower value such as 0.3 for example, rather than the default of 0.5.

Exponential Distribution of Water Table Location

A Uniform Distribution can be used to simulate an equal probability of the Water Table occurring at any location between the Minimum and Maximum Water Table boundaries.

Normalized Standard Deviation

Because the Water Table location is specified using a normalized Random Variable with a range of 0 to 1, the Standard Deviation must also be specified as a Normalized value. Although the concept of a Normalized Standard Deviation may be a bit harder to grasp than the concept of a Normalized Mean, it is very simple, just remember:

• The Statistical Distribution you are defining for the Water Table location is really for a Random Variable with a range of 0 to 1.
• Therefore, define the Normalized Standard Deviation accordingly.
• For example: for a Normal Distribution, the Minimum and Maximum values should be located at approximately 3 Standard Deviations away from the Mean, in order to define a complete (non-truncated) Normal Distribution. For a Random Variable with a Minimum = 0, Mean = 0.5 and Maximum = 1, a Standard Deviation of approximately (0.5/3) = 0.17, will generate normally distributed samples of the Water Table location, between the Minimum and Maximum Water Table boundaries.

Ponded Water and a Random Water Table

If the Maximum Water Table boundary is located ABOVE the slope at any location, and this results in a randomly generated Water Table which is above the slope, then Ponded water is automatically created between the Water Table and the slope, in exactly the same manner, as for a regular (DETERMINISTIC) Water Table.

However, note that when you define the Maximum Water Table boundary above a slope, Ponded Water is NOT graphically displayed on the model. Ponded water will be automatically created and taken into account during the analysis, whenever necessary, but it will not be visible on the model.

Sensitivity Analysis

If you are performing a Sensitivity Analysis, and the Water Table Location is one of the variables you are analyzing, then you must define the Minimum and Maximum Water Table boundaries, as described above for a Probabilistic Analysis. The Sensitivity Analysis will be carried out by uniformly varying the Water Table location between the Minimum and Maximum Water Table boundaries, in 50 equal increments.

For more information about Sensitivity Analysis with Slide2, see the Sensitivity Analysis topic.