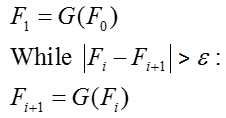Iteration Parameters

The Advanced page in the Project Settings dialog allows you to configure the following Iteration Parameters.

• Check m_alpha
• Min/max lambda (Spencer, GLE, Sarma vertical)
• Initial Trial Value of FS
• Max. Iteration Change in FS
• Min. Iteration FS
• Use Steffensen's Method

The Iteration Parameters are used during the limit equilibrium analysis calculations to determine safety factor.

M_Alpha Check

The variable m_alpha, is the denominator in the equation which is used to calculate the NORMAL force on the base of a slice, during the limit equilibrium calculations. It is dependent on the angle of the slice base (alpha), the friction angle of the material, and the safety factor F, as follows:

The factor of safety calculation is sensitive to the value of m_alpha. It has been suggested (Whitman and Bailey, 1967), that if the value of m_alpha goes below 0.2, for any slice, during the limit equilibrium calculations, the resulting safety factor may be incorrect or misleading. For example:

• m_alpha cannot equal zero, since this gives an infinite normal force, and no safety factor can be calculated.
• If m_alpha is small (but positive), this may lead to the calculation of a large normal force. This may result in a disproportionately large shear resistance and possibly incorrect factor of safety.
• If m_alpha is negative, a negative shear resistance can be calculated. This may lead to low factors of safety. If m_alpha is small (but negative), a large negative normal force will result and may lead to the calculation of a negative safety factor, which is meaningless.

A more complete discussion of issues related to the variable m_alpha can be found in Ching and Fredlund, 1983.

So there are numerous reasons to keep track of the value of m_alpha during the stability calculation. To ensure that the value of m_alpha is NOT ALLOWED to go below a value of 0.2, select the checkbox for "Check m_alpha < 0.2". Any slip surfaces for which m_alpha < 0.2 (on the final iteration of the limit equilibrium calculation), will be reported as INVALID slip surfaces, with an error code of -112 written to the output file.

Surfaces with an error code of -112, will often be deep-seated slip surfaces, with high negative base angle slices in the passive zone (at the toe of the slope). In some cases, you may wish to calculate a safety factor for these slip surfaces.

A value of m_alpha < 0.2, DOES NOT NECESSARILY MEAN THAT THE SAFETY FACTOR IS INCORRECT. In most cases, a safety factor can still be calculated (i.e. the limit equilibrium calculation will converge to an answer). If you wish to analyze such surfaces, then clear the "Check m_alpha < 0.2" checkbox. In this case, m_alpha is allowed to take on any value, except zero (m_alpha cannot equal zero, since the entire stability calculation would then abort).

Min Lambda / Max Lambda

These options are applicable for the Spencer, GLE and Sarma (Vertical Slice) analysis methods. They allow you to set minimum and maximum values of lambda, which limits the minimum and maximum angle of the resultant interslice force computed during the analysis.

Initial Trial Value of FS

By default the initial trial value of Factor of Safety = 1. You may enter a different value if you wish to start with a particular trial value.

Max iteration change in FS

This option allows you to limit the maximum change in Factor of Safety between successive iterations of the limit equilibrium analysis. This may be useful in some cases and allows you to control the rate of convergence. If the change in safety factor is greater than this value between successive iterations, then it will be set equal to this value for the next iteration.

Minimum iteration FS

This option allows you to specify a minimum value of safety factor computed during the analysis. Very low safety factors may indicate zero shear resistance along part of the slip surface. If this checkbox is selected, then slip surfaces with factor of safety below this value will be discarded from the analysis.

Use Steffensen's Method

If this checkbox is selected, then Steffensen's Method will be used during the iteration procedure used to determine the factor of safety. Steffensen's Method is a well-known root-finding method with quadratic convergence properties. In the Slide2 implementation, the results of the previous TWO iterations are used to determine the next value.

• Improvement on Fixed Point Iteration (FPI)
• Incorporates Aitken’s process into FPI
• Aitken’s is an acceleration technique
• Rate of convergence is increased from linear to quadratic without the use of derivatives
• Radius of convergence is increased
• Results in more converged surfaces, and faster speed in reaching these convergences

The algorithm works as follows. If solving for a variable F ensure that function is in form F=G(F). Choose an initial value F0 and a tolerance epsilon. Let i = 0.

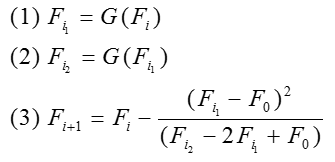
While and repeat until desired tolerance is achieved.

If this checkbox is not selected, then standard Fixed Point Iteration is used: