General Quadratic/Hyperbolic Model (GQ/H)
The Darendeli (2001) study constructs the shear strength - shear strain curves based on the experimentally obtained data. At small strains the data is collected using resonant column tests, and towards the medium shear strain levels the torsional shear test results are used. The values are extrapolated at the large strain levels. This extrapolation may underestimate or overestimate the shear strength at large strains. Therefore, shear strength correction is necessary to account for the correct shear strength at large strains (Phillips and Hashash 2009). General Quadratic/ Hyperbolic model proposed by (Groholski et al. 2016) has a curve fitting scheme that automatically corrects the reference curves (such as Darendeli (2001)) based on the specified shear strength at the large strains (the parameter τmax in Eq. 2). The curve fitting parameters θ1 through θ5 (Eq. 1) are used to preserve the modulus reduction curves obtained from reference studies as much as possible and modifies the large strain values based on the specified large strain shear strength.
The parameters τmax, and θ1 through θ5 are required to construct the shear strength corrected shear strength - shear strain curves. Obtaining τmax is straightforward and user only needs to determine the shear strength of the simulated soil material at large strains. The parameters θ1 through θ5 can be obtained based on the reference study (Groholski et al. 2016). One easy way to obtain these parameters is using RSSeismic (a 1-D nonlinear site response analysis software). The user can create the layered domain in RSSeismic software and select the available reference curve. Upon constructing the layered domain, GQ/H curve fitting routine calculates the shear strength corrected shear strength - shear strain curve and provides the parameters θ1 through θ5. These values can be directly used in soil hysteretic material without necessity to define any reference shear strength - shear strain curve. The material model uses the τmax, 𝐺0, and θ1 through θ5 to construct the shear strength - shear strain curve using the following functions:
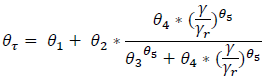 | Eq. 1 |
where, 𝛾𝑟 is the reference strain and is calculated as 𝛾𝑟=𝜏𝑚𝑎𝑥/𝐺0. Once the θτ is determined, the shear strength - shear strain curve is constructed as follows:
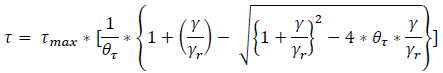 | Eq. 2 |