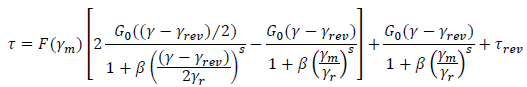Default Hysteretic Re/Unloading Formulation

For Equivalent Linear and Nonlinear analyses, users have the option to select the Default Hysteretic Re/Unloading Formulation:

• Non-masing re/unloading (recommended)
• Masing re/unloading

Masing Rules

When the user wishes to fit a soil curve (i.e. determine the model parameters which most closely match the defined curves), the following options are available:

• MR: Procedure to find the parameters that provide the best fit for the modulus reduction curve with potentially significant mismatch of the damping curve.
• MRD: Procedure to find the parameters that provide the best fit for both the modulus reduction and damping curve.
• DC: Procedure to find the parameters that provide the best fit for the damping curve with potentially significant mismatch of the backbone curve.

Non-Masing Unload-Reload Rules

The non-Masing model included in RSSeismic is the MRDF Pressure-Dependent Hyperbolic model (Phillips and Hashash, 2009). This model is implemented as a reduction factor which effectively alters the Masing rules. By introducing the reduction factor, the modulus reduction and damping curves can be fit simultaneously. The damping behavior is modified as:

𝜉_{𝑀𝑎𝑠𝑖𝑛𝑔𝐻𝑦𝑠𝑡𝑒𝑟𝑒𝑡𝑖𝑐} = 𝐹(𝛾_𝑚𝑎𝑥) ∗ 𝜉_{𝑀𝑎𝑠𝑖𝑛𝑔}

where F(γ_m) is the reduction factor calculated as a function of γ_m,, the maximum shear strain experienced by the soil at any given time, and ξ_Masing is the hysteretic damping calculated using the Masing rules, based on the modulus reduction curve. Two formulations for F(γ_m) are implemented in RSSeismic are:

• MRDF-UIUC
• MRDF-Darendeli

MRDF-UIUC

The MRDF Pressure-Dependent Hyperbolic (Phillips and Hashash, 2009) model available in RSSeismic allows the user to introduce a reduction factor into the hyperbolic model. The reduction factor has the form:

𝐹(𝛾_𝑚) = 𝑃₁−𝑃₂(1−𝐺(𝛾_𝑚) ⁄ 𝐺₀)^𝑃₃

where 𝛾𝑚 is the maximum shear strain experienced at any given time, 𝐺(𝛾_𝑚) is the shear modulus at 𝛾_𝑚, and P₁, P₂, and P₃ are the fitting parameters.

By setting P₁= 1 and P₂= 0, the reduction factor is equal to 1 (regardless of the value of P₃), and the model is reduced to the Extended Masing criteria.

MRDF-Darendeli

The MRDF Pressure-Dependent Hyperbolic model (Phillips and Hashash, 2009) can also be used with alternative formulations for the reduction factor. One alternative is the formulation proposed by Darendeli, 2001. This formulation is an empirically-based modified hyperbolic model to predict the nonlinear dynamic responses of different soil types. The developed model is implemented as a reduction factor with the form:

𝐹(𝛾_𝑚) = 𝑃₁(𝐺(𝛾_𝑚) ⁄ 𝐺₀)^𝑃₂

where 𝛾𝑚 is the maximum shear strain experienced at any given time, 𝐺(𝛾_𝑚) is the shear modulus at 𝛾_𝑚, and P₁ and P₂ are the fitting parameters.

By setting P₁= 1 and P₂= 0, the reduction factor is equal to 1, and the model is reduced to the Extended Masing criteria.

Non-Masing Unload-Reload Formulation

The hyperbolic / pressure-dependent hyperbolic unload-reload equation is modified with the reduction factor, 𝐹(𝛾_𝑚), as follows: