GMP (Green, Mitcher and Polito) Model for Sand
The GMP model (Green et al. 2000) is an energy-based pore pressure generation model. The excess pore pressure is calculated as follows:
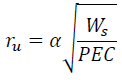 | Eq. 1 |
Table 1: Description of GMP Model Parameters
| VARIABLE | DESCRIPTION |
| ru | Normalized excess pore pressure |
| Ws | Normalized dissipated energy per unit volume of soil |
| PEC | Pseudo energy capacity |
| α | Scale factor |
| v | Degradation parameter |
The dissipated energy, Ws, is calculated as the area beneath the current stress-strain path and has the following functional form:
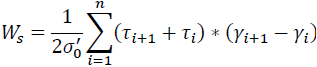 | Eq. 2 |
In RSSeismic, a scale factor “α” is introduced to allow for scaling of the generated excess pore water pressure to match laboratory or field data.
The GMP model is a special case of the Berrill and Davis model (Berrill and Davis, 1985) that has the form ru = α x Wsβ. In GMP model, α and β values are replaced by (1/PEC)0.5 and 0.5 respectively.
The degradation parameter is as described by Matasovic (1993) and uses the same functional form as defined in the Matasovic model for sands (see Pore Water Pressure Degradation topic).
Suggested Values
The determination of the 𝑃𝐸𝐶 calibration parameter can be conducted either via graphical procedure or by use of an empirical relationship. The graphical procedure is described in detail by Green et al. (2000). However, this causes an interruption in the analysis as it requires the construction of the graphical procedure outside of the site response analysis software.
Polito et al. (2008) derived an empirical relationship between 𝑃𝐸𝐶, relative density (𝐷𝑟), and fines content (FC) from a large database of laboratory data on non-plastic silt-sand mixtures, ranging from clean sands to pure silts. The use of this empirical relationship allows the use of the GMP model directly in the nonlinear site response analysis software by removing the need to find the value of 𝑃𝐸𝐶 through graphical procedures. The empirical relationship is defined as:
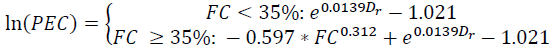 | Eq. 3 |