Stress Computation

The Stress Computation Method determines how the 3-dimensional stress distribution due to loading is calculated.

The Stress Computation Method is specified under the General tab in the Project Settings dialog. Four options are available:

• Boussinesq
• Westergaard
• Multiple Layer
• Vertical Ratio (2:1)
• Vertical Ratio (angle)

Boussinesq Method

The Boussinesq method uses the theory of elasticity to calculate the vertical stress under a point load in a homogeneous, semi-infinite half space:

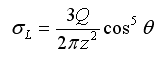
Where is the loading stress at any point and the meaning of the other symbols are as shown in the following figure.

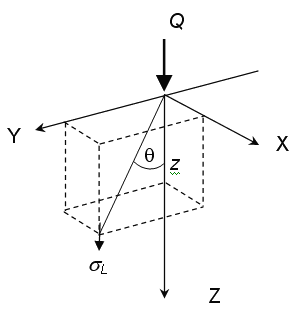
To compute the stresses under a distributed load, the Boussinesq solution is integrated over the area of the footing.

Westergaard Method

The Westergaard stress solution implicitly assumes a layered soil structure, and includes Poisson's ratio in the derivation. This tends to distribute loads over a greater area, compared to the Boussinesq solution.

For further information see the Settle3 Theory Manual.

Multiple Layer Method

The Multiple Layer stress computation method takes into account the stiffness (elastic modulus) of each soil layer when computing the stress distribution due to loading. If the soil layers have significantly different stiffness values, then the resultant stress distribution can be very different from the Boussinesq solution, which assumes homogeneous elastic properties.

If the soil layers all have the same elastic modulus, then the Multiple Layer method should give the same results as the Boussinesq solution.

For further information and references, see the Settle3 Theory Manual.

Vertical Ratio 2:1 Method

The 2:1 method assumes that the zone of influence for an applied rectangular load has a slope of 2:1 as shown in the following figure.

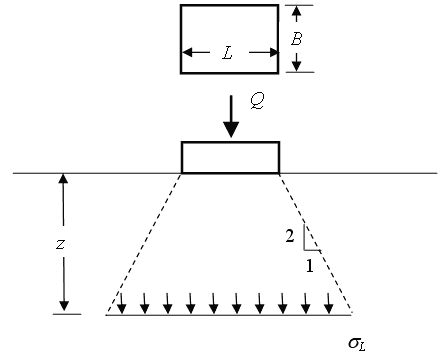
The vertical loading stress at some depth is then calculated by:

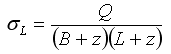
For a non-rectangular footing, the stress is calculated by computing the area of the load at the surface. With increasing depth, the area over which the load is applied increases at a 2:1 ratio and the magnitude of the loading stress decreases correspondingly.

The 2:1 method is included mainly for purposes of comparison with existing calculations, however, its use is generally not recommended for 3-dimensional analysis, due to the simplistic assumption on which the method is based.

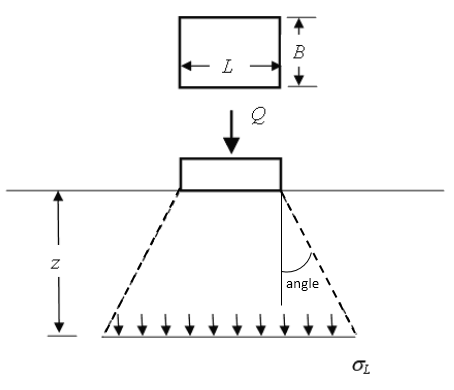
Vertical Ratio (angle)

This method assumes that the zone of influence for an applied rectangular load has a slope which is the angle specified in the Project Settings dialog, as shown in the figure below.

The vertical loading stress at some depth is then calculated by:

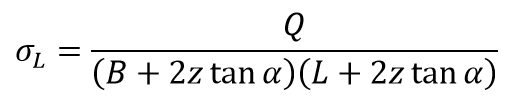
where alpha is the angle.

For a non-rectangular footing, the stress is calculated by computing the area of the load at the surface. With increasing depth, the area over which the load is applied increases at a ratio equal to the specified angle and the magnitude of the loading stress decreases correspondingly.

Note that for vertical ratio (2:1 or angle) stress computation method, any non-uniform loads or embankment loads will be treated as uniform stress distribution due to the nature of simplistic assumptions on which the method is based as discussed above.