Interpolation Methods
There are many different methods which can be used to interpolate values from a grid of data specified at X,Y locations. Interpolation implies that the value of a variable can be determined at any required location, based on the defined values at specified locations.
In Settle3, Interpolation Methods are used for:
- Interpolating the soil profile, if the Multiple Boreholes option in Project Settings is used.
- Interpolating the groundwater level if Grids are being used in the Groundwater Analysis.
- Interpolating with user defined number of surface points in non-horizontal ground surface in project settings.
The following Interpolation Methods are available in Settle3.
Inverse Distance
The Inverse Distance Interpolation method weights every data point according to its distance to the sample point. This scheme is also known as the Shepard method (Shepard, 1968) and can be written in the form:
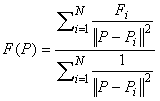
where P is the location of the point to be interpolated, F(P) is the interpolated value, Pi the location of the scattered data, Fi are the scattered data values, and ||P-Pi||2 represents the distance from P to Pi. The main deficiencies of this method are: 1) the local extrema are typically located at the data points and this results in poor shape properties, and 2) undue influence of points which are far away from the sample point.
Thin Plate Spline
The Thin-Plate Spline method utilizes the concept of an infinite thin elastic plate under tension, to determine a spline surface (a smooth 3-dimensional surface which fits through all of the data points). The spline surface is used to determine the sample value at any location (Franke, 1985).
Chugh’s Method
This is an interpolation method based on finding the nearest grid point, in each of the four quadrants with origin centered at the point where the interpolation is required (e.g. at the midpoint of the base of a slice). A plane is then fit through each combination of three quadrant grid points, and an interpolation is performed for each plane. This results in four interpolations, which are then averaged to obtain the final interpolated value at the desired point (Chugh, 1981).
Local Thin Plate Spline
The Local Thin-Plate Spline method is an extension of the Thin-Plate Spline interpolation technique, and is recommended for use with a large number of data points (> 200). The only difference between the methods is that instead of using all the data points for the interpolation, the Local version takes a maximum of 10 closest points to the sample point and fits a spline surface through them. The local spline surface is then used to determine the sample value.
TIN Triangulation
TIN Triangulation (Triangulated Irregular Network) takes the data points and triangulates them using the Delaunay triangulation method. To calculate the value at a sample point, the program first determines which triangle the point lies within. Once the triangle that contains the sample point is found, the interpolated value is calculated using linear interpolation. This is done by calculating the plane equation that fits through the 3 data points at the triangle vertices, then solving for the value using the coordinates of the sample point and the plane equation.
Secondary Interpolation Method
In methods such as the TIN Triangulation and the Chugh method, cases exist where interpolation at a sample point cannot be performed.
- In the case of TIN Triangulation, an interpolation value cannot be calculated if the sample point lies outside the convex hull of the user-defined (grid) data points.
- In the Chugh method, if one or more of the four quadrants surrounding the sample point does not contain any (grid) data points, then an interpolated value cannot be calculated.
In both these cases, a secondary interpolation method is used. By default in Slide, the Local Thin-Plate Spline method is used as the secondary interpolation method. This ensures that an interpolated value is always calculated at a sample point.