Bolt Orientation Efficiency
Bolts which intersect a block can deform in a number of different ways, as shown in Figure 1. As a result, the mechanism of failure of a bolt can be quite complicated. In order to simplify the behavior for the purpose of including support in a limit-equilibrium block analysis program such as RocSlope3, an empirical reinforcement efficiency factor can be used.
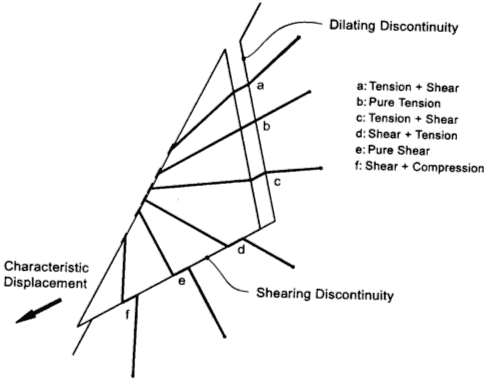
The theoretical tensile capacity of a bolt at any point along its length is determined from the Bolt Force Diagram and the point at which a block plane intersects the bolt. This assumes that a bolt is in pure tension. However, pure tension will only occur if the bolt orientation is aligned exactly with the sliding direction or direction of movement of the block (see Figure 1 - case B).
If a bolt is not in pure tension, but also shear, the effective tensile capacity of the bolt will be reduced. The amount of reduction is given by the Bolt Orientation Efficiency Factor, which may range between zero and one.
- If the bolt efficiency is zero, the bolt has no effect and zero force is placed into the equilibrium equations of the block.
- If the efficiency is one, the bolt is in pure tension and the entire capacity is added as a force in the direction of the bolt in the equilibrium equations of the block.
The Bolt Orientation Efficiency factor is calculated by relating the direction of sliding or movement of the block to the orientation of the bolt. In RocSlope3, there are two different calculation methods.
Cosine Tension / Shear
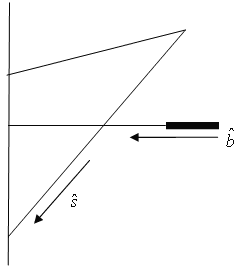
This is the default method in RocSlope3. With reference to Figure 2, the efficiency is calculated as:
e = ̂b̂•ŝ
Where:
b̂ = bolt direction (normalized vector)
ŝ = sliding direction (normalized vector)
e = bolt orientation efficiency
This applies to bolt deformation modes A, B, C, D (see Figure 1). For bolt deformation modes E (pure shear) or F (compression and shear), the bolt efficiency = 0.
Linear Tension / Shear
With the Linear Tension / Shear method, the efficiency is calculated as:
f = ̂b̂•ŝ
ẑ = (0,0,1)
g = |(b̂ x ẑ)•ŝ|
e = f | (f +g)
Where:
b̂ = bolt direction (normalized vector)
ŝ = sliding direction (normalized vector)
f = component of ŝ in direction of b̂
g = component of ŝ perpendicular to b̂
This applies to bolt deformation modes A, B, C, D (see Figure 1). For bolt deformation modes E (pure shear) or F (compression and shear), the bolt efficiency = 0.
Bolt Orientation Efficiency Off
There is also the possibility that the Use Bolt Orientation Efficiency option can be turned off. If you do not wish to use Bolt Efficiency, then clear the Use Bolt Orientation Efficiency checkbox in the Define Bolt Properties dialog.
If Use Bolt Orientation Efficiency is OFF, then the bolt efficiency will equal 1, regardless of the bolt deformation mode (A, B, C, D, E, F; see Figure 1).
Bolt Efficiency and Shear Capacity
Finally, note that the Use Bolt Orientation Efficiency is NOT used in conjunction with the Use Shear Capacity option. If you have selected the Use Shear Strength option, and the bolt deformation mode is D, E or F, so that the Bolt Shear Strength is applied, the Bolt Efficiency DOES NOT multiply the shear strength. The Bolt Efficiency is only used as a factor for the tensile bolt capacity determined from the Bolt Force Diagram.