Triangular Distribution
You may wish to use a Triangular Distribution in some cases, as a rough approximation to a random variable with an unknown distribution.
A Triangular Distribution is specified by its Minimum, Maximum and Mean values. It does not have to be symmetric and can be skewed either to the left or right by entering a mean value greater than or less than the average of the minimum and maximum values.
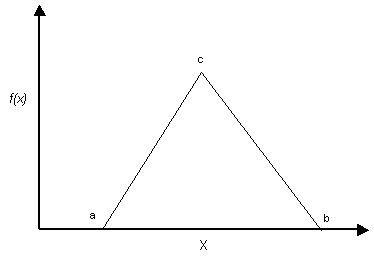
Minimum = a, maximum = b, mode = c. For a symmetric distribution, mean = mode.
For a non-symmetric Triangular Distribution, the mean value is not equal to the mode. The mode is the value of the variable at the peak of the Triangular Distribution. The mean of a Triangular Distribution has the following behaviour:
- In general, the mean of a Triangular Distribution is always given by:
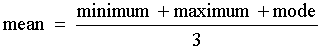
- If the distribution is symmetric, then the mean is equal to the mode.
- For a left Triangular Distribution, the mode = minimum, and the mean = (2*minimum + maximum) / 3.
- For a right Triangular Distribution, the mode = maximum, and the mean = (2*maximum + minimum) / 3.