Waviness Angle
Waviness is a parameter that can be included in calculations of the shear strength of any joint for any of the strength models used in RocSlope3. It accounts for the waviness (undulations) of a joint surface, observed over distances in the order of 1 m to 10 m [Miller, 1988], and has the effect of increasing the Shear Strength of the joint.
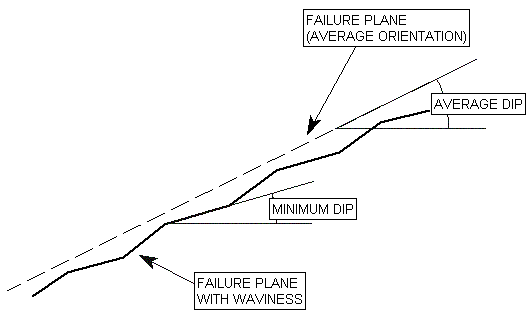
The waviness angle is equal to the AVERAGE dip of the joint, minus the MINIMUM dip of the joint. This is illustrated in the figure below. The waviness angle can be determined by taking a number of failure plane dip measurements, calculating the average dip of the plane and subtracting the minimum dip.
For example, if the average dip = 30 degrees, and the minimum dip = 25 degrees, then the waviness angle = 5 degrees.
Effect of Waviness Angle on Shear Strength
A non-zero waviness angle will increase the effective shear strength of a joint. The implementation of the waviness angle in the shear strength calculation is very simple. The increase in the joint shear strength, due to waviness, is simply equal to:
σx tan (Øw )
where:
σx = normal stress on the joint
Øw = waviness angle
For example, if you are using the Mohr-Coulomb failure criterion, and you have specified a waviness angle (greater than zero), then the shear strength of the joint is given by:
τ = c + σx tan Ø + σx tan Øw
where:
τ = shear strength
c = cohesion
Ø = friction angle
As you can see, the waviness angle is implemented in the same way as the Mohr-Coulomb friction angle. The increased shear strength is proportional to the normal stress and the tangent of the waviness angle. The effect of the waviness angle on shear strength is the same for all strength models used in RocSlope3. Regardless of which strength model you are using in RocSlope3, the failure plane shear strength is simply increased by the amount:
σx tan (Øw )
See the Shear Strength topic for a description of the strength models available in RocSlope3.