Shear Strength
Shear Strength in RocSlope3 is only applicable to the Joint surfaces on which the blocks can slide. Joint Shear Strength refers to the strength of individual Joints or fractures within a rock mass; not the Shear Strength of the intact rock mass.
Joint Shear Strength can be modeled using one of the following Strength Types:
- Mohr-Coulomb
- Barton-Bandis
- Hoek-Brown
- Generalized Hoek-Brown
- Power Curve
Mohr Coulomb
The Mohr-Coulomb model relates Shear Strength and Normal Stress equation, according to:
τ = c + σn tan Ø [Eq. 1]
where:
τ = shear strength
c = cohesion
σn = normal stress
Ø = friction angle
Barton-Bandis
The original Barton equation for the Shear Strength of a rock Joint is given by:
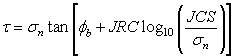
where:
Øb = basic friction angle of the failure surface
JRC = joint roughness coefficient
JCS = joint wall compressive strength [Barton, 1973, 1976]
On the basis of direct shear test results for 130 samples of variably weathered rock joints, Barton and Choubey revised this to:
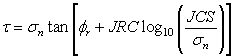
where:
Øy = residual friction angle of the failure surface [Barton and Choubey, 1977]
Barton and Choubey suggest that Icon can be estimated from:
Øy = (Øb - 20) + 20(r | R) [Eq. 2c]
where:
r = Schmidt hammer rebound number on wet and weathered fracture surfaces
R = Schmidt rebound number on dry unweathered sawn surfaces.
Equations 2b and 2c have become part of the Barton-Bandis criterion for rock joint strength and deformability [Barton and Bandis, 1990].
For further information on the Shear Strength of discontinuities, including a discussion of the Barton-Bandis failure criterion parameters, see Practical Rock Engineering: Shear Strength of Discontinuities on the Rocscience website.
Power Curve
The Power Curve model for Shear Strength [Miller, 1988], can be expressed as:
τ = c + a(σn + d)b [Eq. 3]
where:
a, b, and c = parameters which are typically obtained from a least-squares regression fit of data obtained from small-scale shear tests
d = parameter which represents the tensile strength (if included, it must be entered as a positive value)
Hoek-Brown
This is the original Hoek-Brown strength criterion [Hoek and Bray, 1981] which establishes rock mass strength according to the formula:
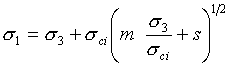
where:
σ1 = major principal stress
σ3 = minor principal stress
σci = uniaxial compressive strength of the intact rock
s = material constants for the rock mass
For the Hoek-Brown (and Generalized Hoek-Brown) criteria, the relationship between Shear Strength and Normal Stress is derived from the Hoek-Brown equations, which are in terms of principal stresses.
The Hoek-Brown criterion is a rock mass failure criterion, applicable to jointed rock masses, and is not applicable to failure along a single joint plane. However, the failure surface in RocSlope3 does not necessarily represent a single discrete joint plane. The use of the Hoek-Brown (or Generalized Hoek-Brown) criterion in RocSlope3 should be considered as follows: the failure plane represents a linear failure surface through a jointed rock mass, rather than a single joint plane. Only under these conditions should the Hoek-Brown failure criterion be applied in RocSlope3.
Generalized Hoek-Brown
The Generalized Hoek-Brown criterion establishes strength according to the formula:
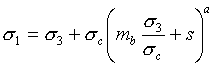
where:
σ1 = major principal stress
σ3 = minor principal stress
σc = uniaxial compressive strength of the intact rock
mb, s, and a = material constants for the rock mass