Fragmentation Overview

Fragmentation in rockfall occurs when a rock impacts the slope and fragments into smaller rock blocks. This process is influenced by several factors, including the presence of pre-existing defects within the rock, the intact rock strength, the mechanical properties of the slope substrate (such as stiffness), and the impact kinematics (e.g. impact velocity and collision geometry). Fragmentation is typically accompanied by a loss in energy. The resulting fragments may travel in various directions, reach different heights, and carry varying amounts of energy. These fragments may also undergo further fragmentation during subsequent impacts. Due to its complexity, rockfall fragmentation remains an active area of research, with ongoing efforts to better understand its mechanics and to develop models for practical application.

RocFall2 presents a recently developed stochastic model for rockfall fragmentation via lump mass simulation. Fragmentation in rockfall can affect the rock trajectory in terms of the runout distances, dispersions in 3D, rock kinetic energies, trajectory heights, and resulting fragment sizes – all of which are important considerations for hazard assessment and protection design. Users may use RocFall2 to analyze rockfall hazard with and without the effects of fragmentation. However, it is recommended that users familiarize themselves with the underlying assumptions and limitations of the fragmentation model to ensure appropriate application and interpretation of results.

Empirical Fragmentation Model

The stochastic fragmentation model available in RocFall2 is fully documented in Guccione et al. (2025). This approach combines experimental, theoretical, and numerical observations with a stochastic prediction of fragmentation occurrence. Experimental observations of artificial spherical rock-like specimens dropped on concrete surface have highlighted key aspects of block fragmentation upon impact, including the relationship between the number, mass, and velocities of fragments relative to the impact velocity (Guccione et al. 2021a, 2021b, 2023).

Whether a rock block survives or fragments upon impact is assessed using a stochastic fragmentation prediction model (also called fragmentation survival probability) proposed by Guccione et al. (2021a). This model accounts for the statistical variability in the tensile strength of the falling block as well as the elasticity of the impacted slope. Input parameters can be derived from standard rock characterization tests: Brazilian tests (BT), also known as indirect tensile tests (ISRM 1978), and unconfined compressive strength (UCS) tests (Bieniawski and Bernede 1979). The fragmentation survival probability is further adjusted for damage accumulated from previous impacts, based on numerical studies conducted on marble spheres (Buzzi et al, 2024).

If an impacting rock does not survive and fractures, then the number and size of fragments are obtained as a function of the impact velocity. The velocity of fragments is determined based on the impact velocity and on the intact secant Young’s modulus of both the rock block and slope, which can be obtained via UCS tests or, in the case of loose materials (e.g. sand or gravel), from confined compression tests (triaxial tests). The energy lost in fragmentation is estimated based on mode I fracture toughness (Kuruppu et al., 2014), if available. If mode I fracture toughness data are not available, the energy lost is approximated as 4% of the impact kinetic energy, based on experimental results by Guccione et al. (2023).

Key assumptions of the Guccione et al. (2025) fragmentation model are summarized as follows:

• Intact specimens: The artificial rock-like specimens were intact samples, and thus the fragmentation model accounts for fracture through the intact rock material and does not account for the effect of defects that may be present in real falling rocks.
• Projection of 3D velocity in 2D: Fragment translational velocities were tracked and formulated for 3D analysis. Given RocFall2 simulates rockfalls in a 2D section, the predicted translational velocities of the fragments are projected onto a 2D plane.
• Simplified impact kinematics: The laboratory specimens were spherical and dropped with minimal rotation, resulting in negligible fragment rotation after impact. Consequently, the modeled impact kinematics are simplified and do not fully consider the influence of rock shape, rotation, and friction at contact. Hence, the fragmentation model is currently limited to lump mass simulation without considering rotation, in which rocks are assumed to be infinitely small particles without the shape and frictional influence that need to be accounted for in rigid body dynamics.
• Mass loss due to fine fragmentation: A 2% mass loss is applied if a rock block fragments upon impact. This mass loss represents the generation of fine particles or powder during crushing at impact. In the field, this mass loss may or may not be applicable, depending on the nature of the geological materials.

The fragmentation model in RocFall2 was verified using experimental data (Guccione et al. 2023, 2025) and real scale in-situ data (Gili et al. 2022; Matas et al. 2020; Prades-Valls et al. 2022) and other historical cases, as documented in the RocFall2 Fragmentation Verification Manual.

Fragmentation Analysis Workflow

Conducting a rockfall analysis and accounting for rock fragmentation in RocFall2 is straightforward. Inputs required for fragmentation analysis can be found in Project Settings, Slope Materials Library, and Rock Type Library, as described below.

Project Settings

1. Select Analysis > Project Settings in the menu.
2. Select the General tab.

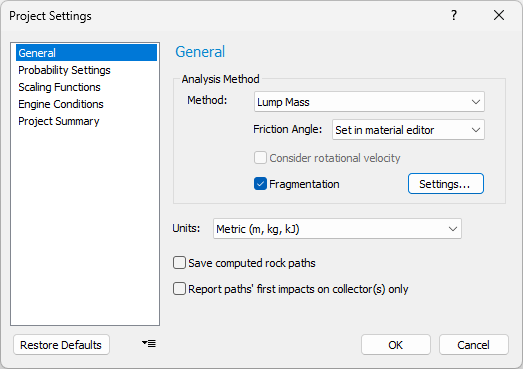
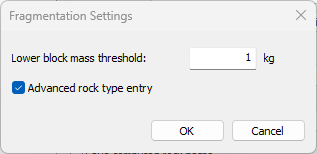
To access fragmentation analysis, select the Lump Mass method. Fragmentation analysis is currently not available for the Rigid Body method. When the fragmentation option is enabled, the Consider rotational velocity option is disabled because the Guccione et al. (2025) fragmentation model does not consider rock rotation. A Settings button will also appear, which grants user access to advanced fragmentation analysis settings. Within the fragmentation settings dialog, the user may input a Lower block mass threshold and select Advanced rock type entry. The Lower block mass threshold controls the lower limit of fragment sizes considered in the fragmentation analysis. Users would typically not be interested in the hazard presented by very fine fragments. Another consideration is that the total number of fragments may grow with each impact and negatively affect the overall computational performance. The Advanced rock type entry permits users to input detailed material characterization for the seeder rock in the Rock Type Library. Users are advised to select Advanced rock type entry only if they have full testing data (UCS, Brazilian, Fracture Toughness) or are interested in conducting their own verification of the fragmentation analysis.

Slope Material Library

1. Select Slope > Slope Material Library in the menu.
2. Select the Fragmentation tab.

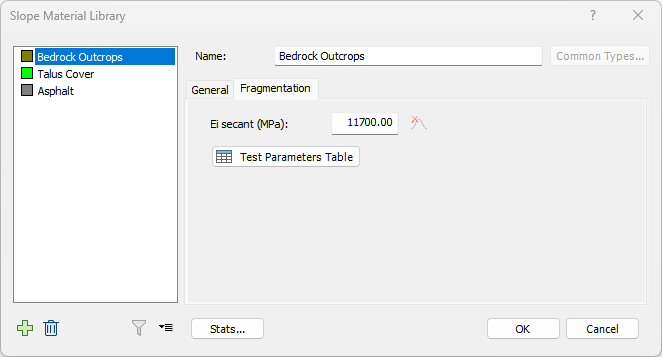
Every slope material requires its own set of material characterization for the fragmentation model, based on UCS testing. The secant modulus of intact samples is a required input. In the absence of test data, users may refer to the Test Parameters Table for published reference values.

Rock Type Library

1. Select Seeder > Rock Type Library in the menu.
2. Select the Fragmentation tab.

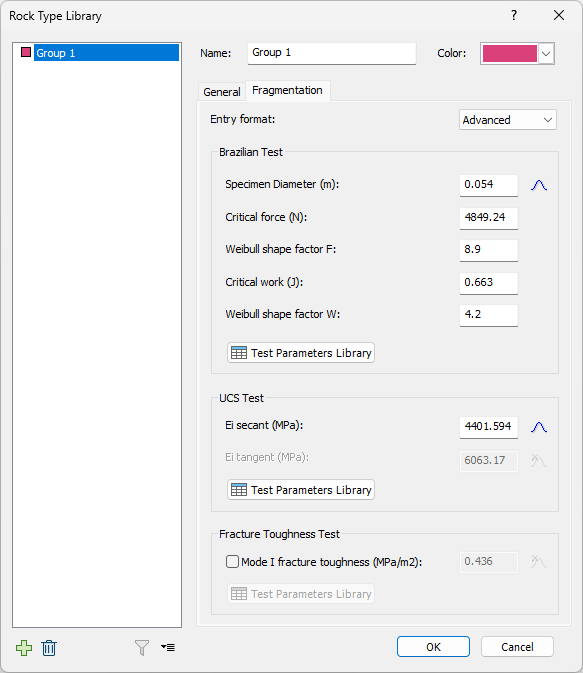
Every rock type requires its own set of material characterization for the fragmentation model, based on UCS testing, Brazilian testing, and optionally, Fracture Toughness Testing. Users have two (2) entry options: 1) a simplified entry form, which is shown on the default view of the Fragmentation tab; or 2) an advanced entry form, accessible via Project Settings with user selection of Advanced rock type entry. The entry options are described below.

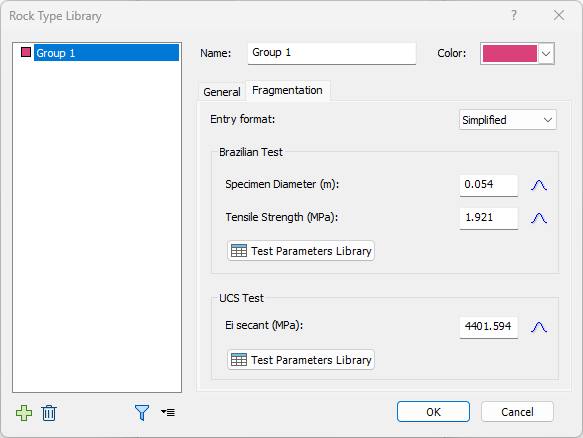
The default entry for rock block material characterization requires only three input parameters and is thus referred to as the simplified entry form. The required inputs are the UCS test intact secant modulus, the Brazilian test specimen diameter, and the Brazilian test tensile strength. In the absence of test data, users may refer to published reference values available via the Test Parameters Table. The simplified entry form is catered towards users who have limited laboratory test data or none at all.

The advanced entry form for rock block material characterization is geared towards advanced users who have actual laboratory test data for interpretation and/or would like to verify the fragmentation analysis. Users would need UCS testing, Brazilian testing, and fracture toughness testing, to obtain specific parameters for the intact secant modulus, intact tangent modulus (optional), Brazilian specimen diameter, critical force, critical work, Weibull shape factors, and mode I fracture toughness (optional).

Whether a user chooses to input via the simplified or advanced entry form should not drastically change analysis results. The simplified entry using Brazilian tensile strength results in the computation of a theoretical force-displacement curve based on Hertz contact theory (Japaridze 2015), from which critical force, critical work, and Weibull shape factors are retrieved (Guccione et al., 2021a, 2022). The differences between the theoretical versus laboratory values typically range between 5% to 20%.

For more details on the rock characterization parameters, please see the following links:

• UCS Test: Bieniawski ZT, Bernede MJ (1979) Suggested methods for determining the uniaxial compressive strength and deformability of rock materials. Int J Rock Mech Min Sci Geomech Abstr. 16(2):137–140. https://doi.org/10.1016/0148-9062(79)91451-7
• Brazilian Test: ISRM (1978) Suggested methods for determining tensile strength of rock materials. Int J Rock Mech Min Sci Geomech Abstr. 15(3):99–103. https:// doi. org/ 10. 1016/ 0148- 9062(78) 90003-7
• Fracture Toughness Test: Kuruppu MD, Obara Y, Ayatollahi MR, Chong KP, Funatsu T (2014) ISRM-suggested method for determining the mode I static fracture toughness using semi-circular bend specimen. Rock Mech Rock Eng. 47(1):267–274. https://doi.org/10.1007/s00603-013-0422-7

Results Interpretation

Users should interpret results for a fragmentation analysis stochastically, as they would typically do for a rockfall analysis without fragmentation. Note that in a rockfall analysis with fragmentation, two (2) new data types become important for interpretation: 1) block mass; and 2) block volume. This is because fragmentation can change the distribution of rock size along a slope. With every occurrence of fragmentation, the number of rocks at any point on the slope could increase, while the size of rocks could decrease. By exposing the block mass and block volume data types for interpretation in conjunction with kinetic energy and height, users can study the effects of fragmentation on hazard and protection sizing requirements at various slope locations.

References

Bieniawski ZT, Bernede MJ (1979) Suggested methods for determining the uniaxial compressive strength and deformability of rock materials. Int J Rock Mech Min Sci Geomech Abstr. 16(2):137–140. https://doi.org/10.1016/0148-9062(79)91451-7

Gili JA, Ruiz-Carulla R, Matas G, Moya J, Prades A, Corominas J, Lantada N, Núñez-Andrés MA, Buill F, Puig C, Martínez-Bofill J, Saló L, Mavrouli O (2022) Rockfalls: analysis of the block fragmentation through field experiments. Landslides. https://doi.org/10.1007/s10346-021-01837-9

Guccione DE, Buzzi O, Thoeni K, Fityus S, Giacomini A (2021) Predicting the fragmentation survival probability of brittle spheres upon impact from statistical distribution of material properties. Int J Rock Mech Min Sci. 142:104768. https://doi.org/10.1016/j.ijrmms.2021.104768

Guccione DE, Thoeni K, Fityus S, Nader F, Giacomini A, Buzzi O (2021) An experimental setup to study the fragmentation of rocks upon impact. Rock Mech Rock Eng. https://doi.org/10.1007/s00603-021-02501-3

Guccione DE, Buzzi O, Thoeni K, Giacomini A, Fityus S (2022) Practical considerations for the application of a survival probability model for rockfall. Aust Geomech J 57(2):115–129

Guccione DE, Giacomini A, Thoeni K, Fityus S, Buzzi O (2023) On the dynamic fragmentation of rock-like spheres: insights into fragment distribution and energy partition. Rock Mech Rock Eng 56(2):847–873. https://doi.org/10.1007/s00603-022-03114-0

Guccione DE, Barros G, Thoeni K, Huang Z, Giacomini A, Buzzi O (2025). A new stochastic rockfall fragmentation approach for lumped mass simulations. Rock Mech Rock Eng. https://doi.org/10.1007/s00603-025-04743-x

Japaridze L. (2015). Stress-deformed state of cylindrical specimens during indirect tensile strength testing. J Rock Mech Geotech Eng. 7(5): 509-518. https://doi.org/10.1016/j.jrmge.2015.06.006

ISRM (1978) Suggested methods for determining tensile strength of rock materials. Int J Rock Mech Min Sci Geomech Abstr. 15(3):99–103. https:// doi. org/ 10. 1016/ 0148- 9062(78) 90003-7

Kuruppu MD, Obara Y, Ayatollahi MR, Chong KP, Funatsu T (2014) ISRM-suggested method for determining the mode I static fracture toughness using semi-circular bend specimen. Rock Mech Rock Eng. 47(1):267–274. https://doi.org/10.1007/s00603-013-0422-7

Matas G, Lantada N, Corominas J, Gili J, Ruiz-Carulla R, Prades A. (2020). Simulation of Full-Scale Rockfall Tests with a Fragmentation Model. Geosciences, 10(5), 168. https://www.mdpi.com/2076-3263/10/5/168

Prades-Valls A, Corominas J, Lantada N, Matas G, Nunez-Andres MA (2022) Capturing rockfall kinematic and fragmentation parameters using high-speed camera system. Eng Geol. 302:106629. https://doi.org/10.1016/j.enggeo.2022.106629