Normal Distribution

The Normal (or Gaussian) distribution is the most common probability density function (PDF) and is generally used for probabilistic studies in geotechnical engineering. Unless there is good reason to use one of the other PDFs available in RocFall, it is recommended that the user choose the Normal PDF.

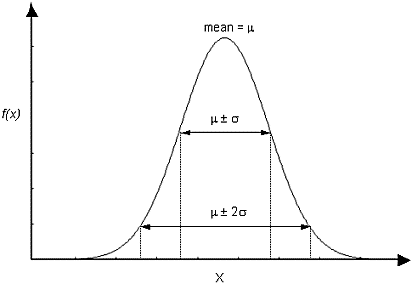
For a Normal distribution:

• 99.74% of samples are within ± (3 x std.dev.)
• 95.44% of samples are within ± (2 x std.dev.)
• 68.27% of samples are within ± (1 x std.dev.)

Normal probability density function, showing standard deviation ranges

Truncated Normal Distribution

A truncated Normal distribution can be defined for a variable by setting the desired minimum and/or maximum values for the variable. For practical purposes, minimum and maximum values that are at least 3 standard deviations away from the mean generate a complete normal distribution. If the minimum / maximum values are less than 3 standard deviations away from the mean, the distribution is visibly truncated.

Estimating a Standard Deviation

For a Normal distribution, 99.73 % of all samples, will fall within 3 Standard Deviations of the mean value. This fact leads to the following rule of thumb (the "Three Sigma Rule"), which allows you to estimate a standard deviation for a normally distributed random variable.

Estimate the highest conceivable value (HCV) of the random variable, and the lowest conceivable value (LCV), and divide the difference between them by six:

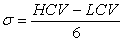
The resulting value can be taken as the Standard Deviation of the Normally Distributed random variable. This is useful if actual data is not available. This and other methods of estimating standard deviation are discussed in (Duncan, 2000).