Joint Water Pressure

To include Joint Water Pressure in the analysis, select the Joint Water Pressure check box in the Input Data dialog. The following Pressure Distribution options will be available:

• Filled Fissures
• %Filled Fissures
• Custom Pressure
• Peak Pressure – Beneath Crest
• Peak Pressure – Toe
• Peak Pressure – Mid Height

Filled Fissures

The Filled Fissures option assumes that extreme conditions of very heavy rainfall have occurred and that in consequence, the fissures (Joint Set 1, Joint Set 2, Tension Crack, Basal Joint) are completely full of water. Further, it is assumed that the pressure varies from zero at the free faces to a maximum value at some point on the line of intersection of the failure planes.

For the Filled Fissures option, SWedge calculates average values of water pressure on the failure planes as follows [Hoek & Bray (1981)]:

WITH NO TENSION CRACK

Eqn. 1

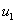where: and 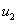are the average values of water pressure on failure planes 1 and 2

= unit weight of water

= total height of the wedge

WITH TENSION CRACK

Eqn. 2

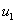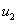where: , and 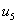are the average values of water pressure on the failure planes 1 and 2, and the tension crack, respectively

= unit weight of water

= depth of bottom vertex of the tension crack below the upper ground surface

The above formulae are simple estimations which are useful in the absence of more precise information.

Notes:

• To simulate intermediate water pressures, you can effectively vary the water pressure (as seen in Equations 1 and 2) by varying the unit weight of water between zero and the actual unit weight. This allows you to perform a sensitivity analysis on the effect of water pressure on the safety factor of the wedge. However, the % Filled Fissures option can also be used, as described below.
• To simulate "dry" joints, you can clear the Joint Water Pressure check box in the Input Data dialog, or enter a Unit Weight of zero.

% Filled Fissures

The % Filled Fissures option allows you to specify the average height of water in the fissures, as a percentage of the completely water-filled state.

For example, if % Filled = 50 % :

There are two options for defining the percent filled - Percent Filled and Percent Slope Height.

PERCENT FILLED

The Percent Filled option allows you to define the percent filled water level with respect to the wedge height.

• For a wedge with no Tension Crack, Percent Filled is with respect to the wedge Slope face height. The upper water surface is a plane parallel to the Upper Slope face and intersects the wedge Slope face at the percentage (i.e., Percent Filled) of the wedge Slope face height specified.
• If your model includes a Tension Crack then the Percent Filled is with respect to the Tension Crack height (Percent Filled TC).

PERCENT SLOPE HEIGHT

The Percent Slope Height option allows you to define the percent filled water level with respect to the slope height. This is useful for Probabilistic Analysis or for scaled wedges when wedges smaller than the slope height are generated, and you wish to simulate the actual water level in the slope. For example, a small wedge near the crest may be entirely above the water elevation defined by the percent slope height (i.e. dry, zero water pressure) whereas a larger wedge may be partially below the water elevation defined by the percent slope height (i.e. non-zero water pressure).

Custom Pressure

The Custom Water Pressure option allows you to specify the actual average water pressure on each plane, independently. This may be useful if actual water pressure data is available on the failure planes of the wedge. However, remember that these are still average values, and only one value may be specified for each plane (Joint 1, Joint 2, Tension Crack, Basal Joint).

Peak Pressure - Beneath Crest

This option assumes a distribution of water pressure such that the peak (maximum) pressure occurs directly beneath the crest of the slope and decreases linearly from the peak value to zero at the toe and upper face.

Peak Pressure - Toe

This option assumes a distribution of water pressure such that the peak (maximum) pressure occurs at the toe of the slope or wedge, and decreases linearly from the peak value to zero at the upper face.

Peak Pressure - Mid Height

This option assumes a distribution of water pressure such that the peak (maximum) pressure occurs at the mid-height of the slope or wedge and decreases linearly from the peak value to zero at the toe and upper face.

Hu

The Hu parameter is simply a factor between 0 and 1 by which the nominal calculated water pressure is multiplied to obtain the actual pressure.

• The default value (Hu = 1) indicates hydrostatic conditions
• Hu = 0 would be equivalent to a dry slope (zero pressure)
• Intermediate values of Hu (between 0 and 1) could be used to simulate head loss due to groundwater seepage if water flow is occurring in the rock slope.

The water pressure values calculated from the pressure distribution models described above are multiplied by the Hu factor to obtain the final pressure used in the wedge stability calculations. The Hu parameter in SWedge is the same as defined in the Rocscience programs Slide2 and RS2.

The Hu parameter is applicable for all pressure distribution models except the Custom Pressure option.