Random Variables
In order to carry out a Probabilistic analysis with RocTopple, you must define at least one input parameter as a random variable. The following input parameters can be defined as random variables:
Defining Random Variables
To define an input parameter as a random variable, select a statistical distribution for the variable (e.g., Normal, Uniform, etc.) and enter the required statistical parameters (e.g., mean, standard deviation, minimum and maximum values).
- Click the Quick-Stats button
next to the variable in the corresponding input dialog (Input Data, Add/Edit Spot Bolt, Add/Edit Load, Water Pressure).
A popup dialog appears allowing you to select a Distribution and enter the standard deviation, relative minimum, and relative maximum. This option is handy for quickly defining statistics for individual variables.
For details on defining statistical distributions, standard deviation, and minimum/maximum values, see Overview of Statistical Distributions in RocTopple.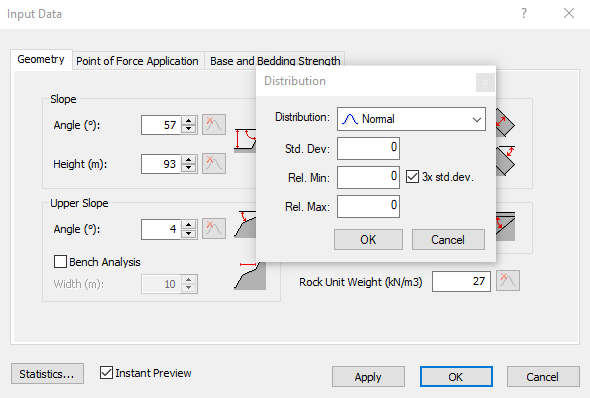
After you have selected a distribution, the button changes to indicate the type of distribution selected (e.g., for a Normal Distribution, the button will show as
). In addition, mousing over the button displays a popup showing the input.
NOTE: When defining Geometry and Strength variables, you also have the option of using the Statistics button
at the bottom of the Input Data dialog to define multiple random variables at a time.
How are the Random Variables used in the Analysis?
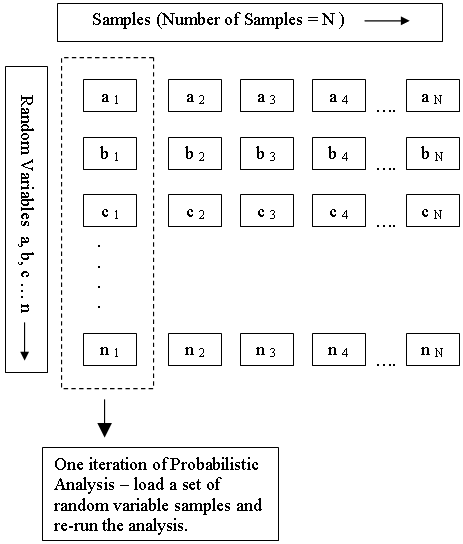
Each input parameter that is defined as a random variable is sampled according to the statistical distribution you have defined for the variable and the Sampling Method and Number of Samples selected in the Project Settings dialog. This generates N values of each random variable (where N = Number of Samples).
As shown in the following diagram, each iteration of the Probabilistic analysis is carried out by loading a new set of random variable samples and re-running the analysis. This is repeated N times.
