Planar Sliding

The Planar Sliding Kinematic Analysis failure mode is a test for sliding on a single plane.

The key elements of the Planar Sliding Kinematic Analysis are:

• Daylighting condition for planes
• Pole Friction cone (angle measured from center of stereonet)
• Lateral limits (optional)

For Planar Sliding you can use either Pole Vector Mode or Dip Vector Mode. The results are equivalent regardless of the vector mode.

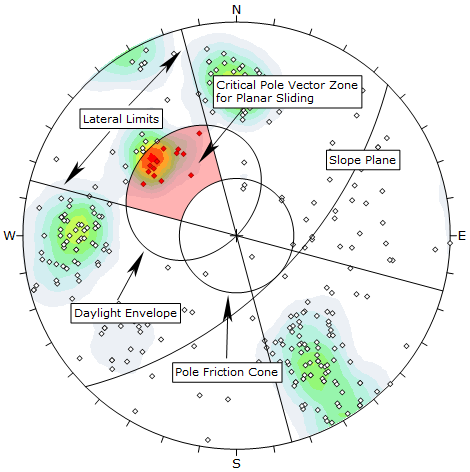
Planar Sliding Kinematic Analysis, pole vector mode

Pole Vector Mode

To carry out Planar Sliding analysis using pole vectors, the Pole Vector Mode must be in effect. This can be selected from the toolbar, the View menu or the Kinematic Analysis dialog ( Vector Mode = Pole).

For Planar Sliding using pole vectors, the critical zone for Planar Sliding is defined by the region:

• INSIDE the daylight envelope and
• OUTSIDE the POLE friction cone and
• INSIDE the lateral limits (if lateral limits are in effect)

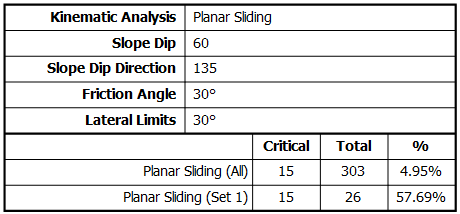
All poles that plot in this region represent a risk of Planar Sliding. This is illustrated in the above figure. In this example, the Friction Angle = 30° , Slope Dip = 60° , Slope Dip Direction = 135° , Lateral Limits = 30° (plus/minus).

Dip Vector Mode

To carry out Planar Sliding analysis using dip vectors, the Dip Vector Mode must be in effect. This can be selected from the toolbar, the View menu or the Kinematic Analysis dialog ( Vector Mode = Dip).

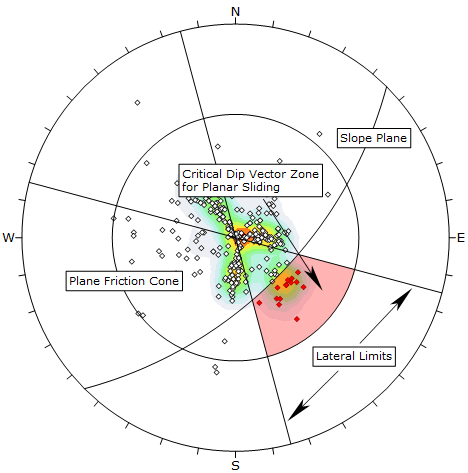
For Planar Sliding using dip vectors, the critical zone for Planar Sliding is defined by the region:

• OUTSIDE the slope plane (daylight condition)
• INSIDE the PLANE friction cone and
• INSIDE the lateral limits (if lateral limits are in effect)

All dip vectors that plot in this region represent a risk of Planar Sliding. This is illustrated in the figure below. The input is the same as the pole vector example above.

Planar Sliding Kinematic Analysis, dip vector mode

Daylight Envelope / Slope Plane

For Planar Sliding, the daylighting condition can be defined either by a daylight envelope (when considering pole vectors) or by the plane itself (when considering dip vectors).

• When considering pole vectors, all pole vectors that fall within the Daylight Envelope (of the slope plane) represent planes which can kinematically daylight from the slope (i.e., the dip vectors of these planes all point "out" from the slope plane).
• When considering dip vectors, all dip vectors that fall outside the slope plane (great circle) represent planes which can kinematically daylight from the slope.

These two criteria are exactly equivalent. All poles that fall within a daylight envelope, are represented by corresponding dip vectors outside the slope plane. In fact, the Daylight Envelope itself is defined by all possible pole vectors whose dip vectors lie exactly on the slope plane (i.e., parallel to the slope plane).

Friction Cone

A friction cone defines the limits of frictional stability on a stereonet. It is important to note the following:

• When considering pole vectors, we use a Pole Friction Cone, and the friction angle is measured from the CENTER of the stereonet. All poles OUTSIDE of the Pole Friction Cone represent planes which dip steeper than the friction angle, and can slide if kinematically possible. The cone angle for a Pole Friction Cone = friction angle.
• When considering dip vectors (or intersections), we use a Plane Friction Cone, and the friction angle is measured from the EQUATOR (perimeter) of the stereonet. All dip vectors INSIDE the Plane Friction Cone represent planes which dip steeper than the friction angle, and can slide if kinematically possible. The cone angle for a Plane Friction Cone = 90° - friction angle.

You can see the difference in the above figures. In both cases, the friction angle = 30° . For the pole vector plot the 30° is measured from the stereonet center; for the dip vector plot the 30° is measured from the stereonet perimeter (the cone angle in this case = 90° - 30° = 60°).

Lateral Limits

The daylighting conditions described above for planar failure, represent theoretical limits of all possible planes which can daylight from a slope face.

In practice it has been observed that planar failure tends to occur only if the dip direction of a plane is within a certain angular range of the slope face dip direction. Typically a value of 20° to 30° is used based on empirical observations ( Goodman 1980, Hudson and Harrison 1997).

You can define the lateral limits for planar failure in the Sidebar or the Kinematic Analysis dialog. The lateral limits define two straight lines through the center of the stereonet, at plus/minus the specified angle from the slope dip direction. The lateral limits add a further restriction to the critical zone for Planar Sliding (poles or dip vectors must be within the lateral limits in order to slide).

Lateral Limits

In the Kinematic Analysis dialog for Failure Mode dropdown list you will notice a Planar Sliding (No Limits) option. If you do not want to use lateral limits, you can choose this option. In this case, the lateral limits option will be disabled (you will not be able to input a value, and the lateral limits will not be displayed or used for the Planar Sliding Kinematic Analysis).

If the lateral limits are not considered, then the entire daylight envelope will be considered kinematically valid. All poles within the daylight envelope (or all dip vectors outside the slope plane) will be considered for Planar Sliding. This represents a worst case and most conservative scenario in which all theoretically possible planes are considered for Planar Sliding.

Alternatively, you can select the Planar Sliding (No Limits) option from the Sidebar.

Planar Sliding Results

Planar Sliding analysis results are displayed in the Legend.

• The number of poles (or dip vectors) within the critical zone are counted.
• Results are expressed as a percentage of all poles in the file, and as a percentage of poles within individual sets (if sets are defined).

These percentages give an estimate of "probability of failure" with respect to all planes in the file, and with respect to all planes in individual sets. It does not matter whether you are viewing poles or dip vectors, the results are identical since the critical zones are equivalent for pole or dip vectors.

NOTE: A detailed summary of all Kinematic Analysis results for all failure modes is available in the Info Viewer.

Planar Sliding Assumptions

An important assumption regarding “pure” Planar Sliding on a single plane, is that release planes are assumed to exist (e.g., lateral joints, tension cracks or other mechanism) which allow a Planar Sliding failure to occur.

Such release planes are not explicitly modeled in the Planar Sliding Kinematic Analysis but you should be aware that some release mechanism must exist to allow a block sliding on one plane to be removed from the slope. Planar Sliding can be considered a special case of Wedge Sliding where sliding takes place on only one plane, and other planes act as release planes.