Wedge Sliding

The Wedge Sliding Kinematic Analysis failure mode is a test for sliding of wedges formed by the intersection of two planes.

The key elements of Wedge Sliding Kinematic Analysis are:

• Slope Plane
• Intersection plotting
• Plane friction cone (angle measured from perimeter of stereonet)

Wedges can slide on two planes (along the line of intersection) or on one plane (if one plane has a more favourable orientation for sliding than the line of intersection). Wedge Sliding is based on the analysis of intersections. Dip vectors of individual planes are also considered to determine if wedges slide on two planes or one plane. Pole vectors are not used.

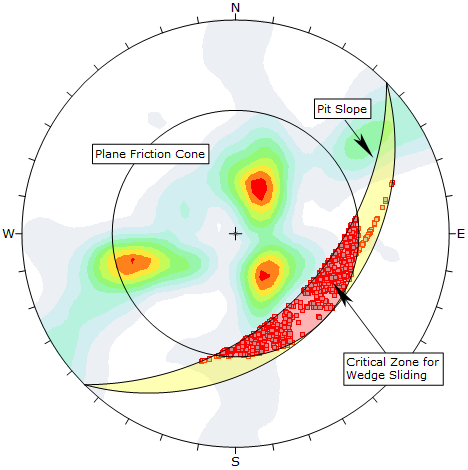
Wedge Sliding Kinematic Analysis, intersection points and contours

Intersection Plotting

When two joint planes intersect, they can form a wedge which can slide out of the slope (depending on kinematic and frictional considerations). The intersection of two planes forms a line in 3-dimensional space. The trend/plunge of the line plots as a single point on a stereonet which we refer to as an intersection.

Wedge Sliding Kinematic Analysis is based on the analysis of intersections. If an intersection point satisfies the frictional and kinematic conditions for sliding then it represents a risk of Wedge Sliding.

In Dips there are several different options for the display of intersections on the stereonet. You can plot:

• The intersection of ALL planes in the file (Grid Data Planes)
• Contours of all intersections (Grid Data Planes)
• Intersections of major planes (i.e., Mean Set Planes and/or User Planes)

In the above figure, the critical intersections of all Grid Data Planes are highlighted in the critical zone, and intersection contours are also displayed. Since the maximum contour concentrations do not overlap the critical zone Wedge Sliding is not likely to be a problem for this example.

See the Intersections Overview topic for more information.

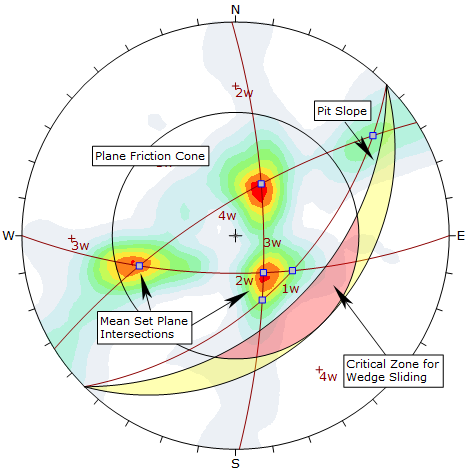
Wedge analysis using mean set plane intersections and contours

Primary Critical Zone for Wedge Sliding

The primary critical zone for Wedge Sliding is the crescent shaped area:

• INSIDE the plane friction cone and
• OUTSIDE the slope plane

Intersections which plot in this zone represent wedges which satisfy frictional and kinematic conditions for sliding. This is highlighted in red in the above figure.

Sliding on Two Planes or One Plane

Depending on the wedge geometry, a wedge may slide along the line of intersection (i.e., on two planes) or on one plane. Sliding on one plane can occur when the dip vector of one of the wedge planes has a more favourable orientation for sliding than the line of intersection.

NOTE: Other failure modes such as rotational sliding or toppling are not considered in this analysis.

Sliding on two planes or one plane is not directly highlighted on the stereonet, however a complete summary of Wedge Sliding results is available in the Info Viewer and can also be exported to Excel.

NOTE:

• In the primary critical zone, wedges can slide on either two planes or one plane.
• In the secondary critical zone, wedges always slide on one plane.

For sliding on a single plane, the dip vector of the sliding plane must be in the primary critical zone. This is the same criteria used for Planar Sliding (with no lateral limits). However note that critical dip vectors are not displayed on the stereonet for wedge analysis, only the critical intersections are plotted.

Secondary Critical Zone for Wedge Sliding

The secondary critical zone for Wedge Sliding is the area between the slope plane and a plane (great circle) inclined at the friction angle (the two areas highlighted in yellow in the above figure, on either side of the primary critical zone). Critical intersections which plot in these two zones always represent wedges which slide on one joint plane. In this region, the intersections are actually inclined at LESS THAN the friction angle, but sliding can take place on a single joint plane which has a dip vector greater than the friction angle.

Friction Cone

A friction cone defines the limits of frictional stability on a stereonet. For Wedge Sliding analysis we use a Plane Friction Cone.

When considering intersections (or dip vectors) the friction angle is measured from the EQUATOR (perimeter) of the stereonet. All intersections or dip vectors INSIDE the Plane Friction Cone represent wedges or planes which dip steeper than the friction angle, and can slide if kinematically possible. The cone angle for a Plane Friction Cone = 90° - friction angle.

For kinematic wedge analysis, it is assumed that both sliding planes have the same friction angle.

Lateral Limits

For Wedge Sliding analysis we do not consider lateral limits. Since the second joint plane allows an extra degree of freedom of movement, it is possible for wedges to slide over the entire lateral range. The second joint plane may act as a sliding plane or a release plane.

Wedge Sliding Results

Wedge Sliding analysis results are displayed in the Legend for the currently displayed intersection type (i.e., Grid Data Planes, Mean Set Planes, User Planes)

• The number of intersections within the critical zone is counted.
• Results are expressed as a percentage of all intersections.

This percentage gives an estimate of "probability of failure" with respect to the total number of intersections for the currently displayed intersection type.

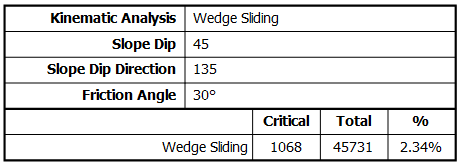
NOTE: Currently, the Legend and stereonet do not identify Wedge Sliding on two planes or one plane. However the Info Viewer provides a detailed breakdown of Wedge Sliding on two planes or one for all intersection types. Furthermore, detailed Kinematic Analysis results can be exported to Excel with the Export Data to Excel option in the File menu.