Beta Distribution

The Beta distribution is a very versatile function which can be used to model several different shapes of probability density curves, as shown below.

Beta (a1, a2) density functions [Law & Kelton (1991)]

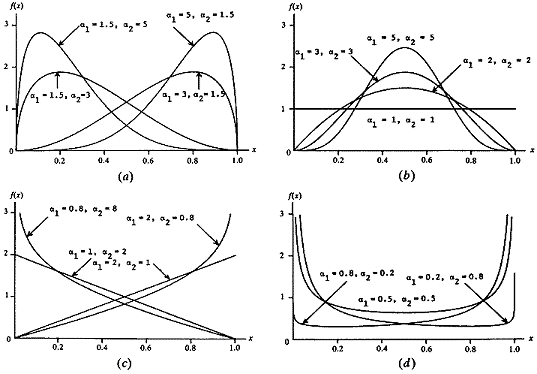
The form of the Beta distribution is determined by the shape parameters a1 and a2. Both a1 and a2 are always > 0. The relationship between the Beta distribution shape parameters and the CPillar input data (mean and standard deviation) is as follows:

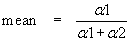
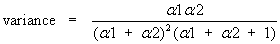
The standard deviation is the positive square root of the variance.

Note that the above equations apply to a beta random variable on [0,1]. To rescale and relocate to obtain a beta random variable on [a,b] of the same shape, use the transformation a + (b–a)X.