Reliability Index

In addition to the Probability of Failure, another commonly used probabilistic measure of safety is the Reliability Index. The Reliability Index is listed in the RocPlane Info Viewer and Sidebar, and is defined as follows.

If one assumes that the distribution of safety factors, after a probabilistic analysis, is normally distributed (i.e. has a Normal Distribution), then Equation 1 is used to calculate the Reliability Index:

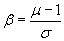Eqn. 1

where:

b = Reliability Index,

m = Mean Factor of Safety,

s = Standard Deviation of FS

As can be seen from Equation 1, the Reliability Index represents the number of standard deviations that separate the mean Factor of Safety, from the critical Factor of Safety ( = 1 ).

• As a rule of thumb, the Reliability Index should be at least 3 or greater, to have reasonable assurance of a safe slope design.
• A Reliability Index = 0, implies that the Mean Factor of Safety = 1.
• A negative Reliability Index indicates a Mean Factor of Safety less than 1.

If one assumes that the distribution of safety factors, after a probabilistic analysis, is lognormally distributed (i.e. has a Lognormal Distribution), then Equation 2 is used to calculate the Reliability Index:

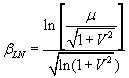Eqn. 2

where:

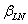= lognormal Reliability Index

m = Mean Factor of Safety

V = coefficient of variation of Factor of Safety = s / m

s = Standard Deviation of FS

In reality, the Factor of Safety distribution is often best fit by a Lognormal rather than a Normal Distribution, and therefore Equation 2 is frequently used to calculate the (lognormal) Reliability Index. Remember that the Lognormal Distribution is only applicable for variables which are always positive, which is the case for Factor of Safety.

The Reliability Index information can be found in the Info Viewer and Sidebar, and is reported for both the Normal (Equation 1) and Lognormal (Equation 2) assumptions.