Failure Shear Strength
A critical assumption in planar slope stability analysis involves the shear strength of the sliding surface. There are several models in rock engineering that establish the relationship between the shear strength of a sliding surface and the effective normal stress acting on the plane. RocPlane offers the following widely accepted shear strength models:
Mohr-Coulomb
In this model the relationship between the shear strength, t, of the failure plane and the normal stress, 
, acting on the plane is represented by the Mohr-Coulomb equation:
Eqn.1
where 
is the friction angle of the failure plane and c is the cohesion.
Barton-Bandis
The original Barton equation for the shear strength of a rock joint is given by E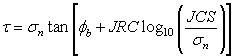qn.2:
Eqn.2
where 
is the basic friction angle of the failure surface, JRC is the joint roughness coefficient, and JCS is the joint wall compressive strength [Barton, 1973, 1976]. On the basis of direct shear test results for 130 samples of variably weathered rock joints, this was later revised to Eqn.3:
Eqn.3
where 
is the residual friction angle of the failure surface [Barton and Choubey, 1977]. Barton and Choubey suggest that can be estimated from Eqn.4:
Eqn.4
where r is the Schmidt hammer rebound number on wet and weathered fracture surfaces and R is the Schmidt rebound number on dry unweathered sawn surfaces. Equations 3 and 4 have become part of the Barton-Bandis criterion for rock joint strength and deformability [Barton and Bandis, 1990].
For further information on the shear strength of discontinuities, including a discussion of the Barton-Bandis failure criterion parameters, see Practical Rock Engineering (Chapter 4: Shear Strength of Discontinuities) on the Rocscience website.
Hoek-Brown
This is the original Hoek-Brown strength criterion [Hoek and Bray, 1981] which establishes rock mass strength according to the formula:
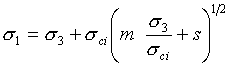Eqn.5
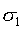is the major principal stress, 
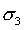is the minor principal stress, 
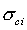is the uniaxial compressive strength of the intact rock, and m and s are material constants for the rock mass.For the Hoek-Brown (and Generalized Hoek-Brown) criteria, the relationship between shear strength and normal stress is derived from the Hoek-Brown equations, which are in terms of principal stresses.
Generalized Hoek-Brown
The Generalized Hoek-Brown criterion establishes strength according to the formula:
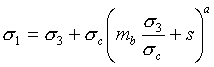Eqn.6
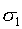is the major principal stress, 
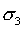is the minor principal stress, 
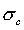is the uniaxial compressive strength of the intact rock, 
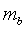is a material constant for the rock mass, and s and a are constants dependent on the characteristics of the rock mass.If you are using the Generalized Hoek-Brown criterion, you can estimate the parameters of the Generalized Hoek-Brown equation, by selecting the GSI button in the dialog. This will display a Parameter Calculator dialog, which allows you to estimate the equation parameters from values of intact rock constant mi, and GSI (Geological Strength Index). Furthermore, within the Parameter Calculator dialog, you may access dialogs for the estimation of mi based on rock type, and the estimation of GSI based on rock structure and surface conditions.
Power Curve
The Power Curve model for shear-strength, 
, of a plane is given by the relationship:
Eqn.7
Waviness Angle
Waviness is a parameter that can be included in calculations of the shear strength of the failure plane, for any of the strength models used in RocPlane. It accounts for the waviness (undulations) of the failure plane surface, observed over distances on the order of 1 m to 10 m [Miller, 1988]. A non-zero waviness angle will always increase the effective shear strength of the failure plane, regardless of the strength model which is in use.
Notes:
- In the Input Data dialog, the waviness angle is specified along with the Failure Plane orientation. The waviness angle is NOT specified under the Strength tab, although it is a strength related parameter.
- For an illustration of the waviness angle, and its effect on shear strength, see the Failure Plane topic for further information.