Rock Mass Modulus

Rock Mass Modulus:

If you are using the Generalized Hoek-Brown strength criterion in RocData, one of the rock mass parameters which is automatically calculated and displayed in the data legend, is the deformation modulus.

Rock mass parameters are shown below in failure range tab.

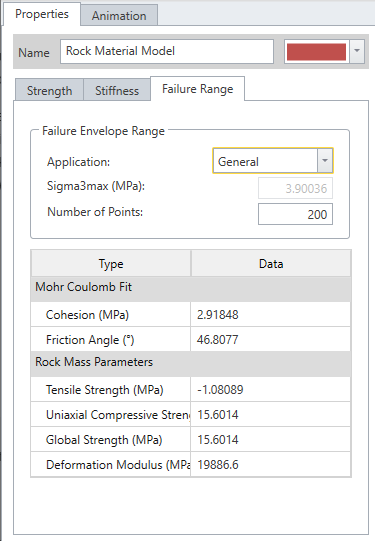
The deformation modulus (Young's Modulus) of a rock mass is often not a well known or easily measured parameter. However, it is a required input parameter for different types of numerical analyses (e.g. finite element stress analysis), therefore it is very important to obtain realistic values of deformation modulus for any analysis which involves deformations.

Several researchers have proposed empirical relationships for estimating the rock mass deformation modulus on the basis of classification schemes. The methods available in RSdata represent the most recent findings, and are based on the GSI rock mass classification scheme and the Generalized Hoek-Brown strength criterion. The rock mass modulus in RocData is calculated according to the currently selected Modulus Estimation Method in the Define Material Model dialog and select GSI calculator.

You may select one of the following three options:

• Generalized Hoek & Diederichs (2006)

• Simplified Hoek & Diederichs (2006)
• Hoek, Carranza-Torres, Corkum (2002)

The applicable equations are given below.

NOTE: the Generalized Hoek & Diederichs (2006) method is the default and recommended modulus estimation method in RocData. The other two methods are available for comparative purposes, but their use is no longer recommended.

Generalized Hoek & Diederichs (2006)

The generalized Hoek and Diederichs equation (Hoek & Diederichs (2006)) utilizes the modulus of the intact rock, GSI and D to compute the rock mass modulus. The modulus is calculated in MPa.

Eqn.1

If you choose this method, then you must enter the intact rock modulus (Ei)

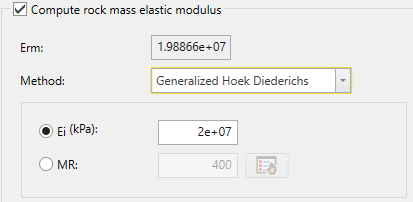
You can enter the intact rock modulus directly, or you can enter the modulus ratio (MR). Intact modulus (Ei) is equal to the modulus ratio (MR) multiplied by the uniaxial compressive strength of the intact rock (sigci).

Ei = MR (sigci) Eqn.2

If you are using the modulus ratio (MR) option, then the value of Ei is automatically calculated using the current values of MR and sigci entered in the Sidebar (e.g. if you change sigci or MR, then Ei will automatically be re-calculated according to Equation 2).

TIP: you can select the suggestion button beside the edit box to estimate the modulus ratio according to rock type.

Simplified Hoek & Diederichs (2006)

The Simplified Hoek & Diederichs equation for rock mass modulus, (Hoek & Diederichs (2006)), only requires GSI and D (Disturbance Factor) as input parameters. The modulus is calculated in MPa.

Eqn.3

This equation can be used if reliable values of intact rock modulus are NOT available.

Hoek, Carranza-Torres, Corkum (2002)

The Hoek, Carranza-Torres and Corkum equation for rock mass modulus (Hoek, Carranza-Torres and Corkum (2002)), uses the uniaxial compressive strength of the intact rock (sigci), GSI and D.

For sigci <= 100 MPa, Equation 4 is used:

Eqn.4

For sigci > 100 MPa, Equation 5 is used:

Eqn.5

The modulus is calculated in GPa.