Calibrate

The Calibrate option can be accessed by selecting Calibrate > Calibrate or by clicking on the Calibrate icon in the toolbar.

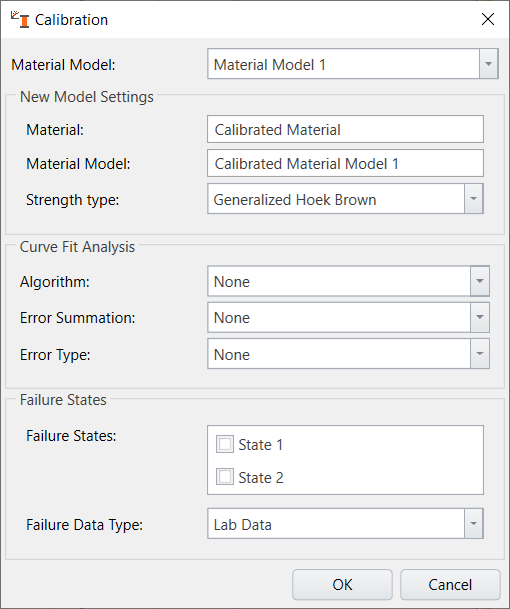
After the calibration, you can see the corresponding results after curve-fit analysis by selecting on the calibrated model and selecting properties as shown below (example from Generalized Hoek-brown tutorial).

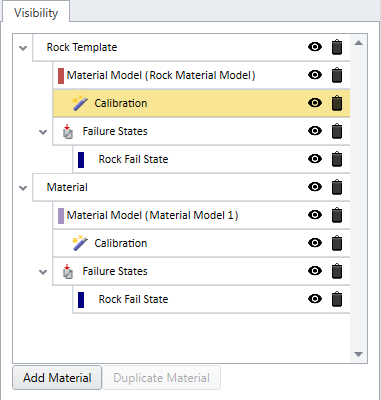
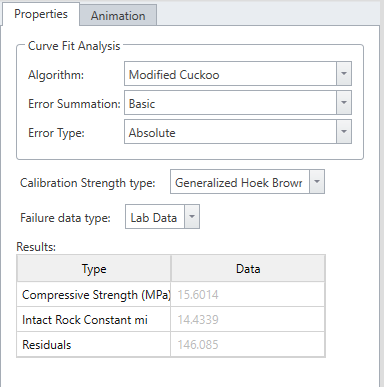
As it shows, the calibration strength type of Generazlied Hoek-Brown, the results with mi, compressive strength, and residual values are shown below.

• Linear Regression
• Modified Cuckoo
• Levenberg-Marquardt
• Simplex

RSData also provides the following methods for summing the error (between data and fitted curve):

• Vertical
• Parabolic
• Basic
• Generalized Fairhurst

Errors or residuals can either be absolute or relative.

These options can be explored in the dropdown menu under Error summation in calibration option. The options apply to the currently selected material. Note that these options are not all available for the selected strength criterion for calibration, but for each strength criterion there are at least two techniques for fitting the criterion to the test data. The following table summarizes the calibration methods available for the different strength models.

	Hoek-Brown Lab Data	Hoek-Brown Rock Mass Data	Mohr-Coulomb	Barton-Bandis	Power Curve
Curve Fit Algorithm
Linear Regression	x		x
Modified Cuckoo	x	x
LevenBerg-Marquardt	x	x	x	x	x
Simplex	x	x		x	x
User Defined	x
Method of Error Summation
Vertical	x	x	x	x	x

Parabolic Tensile	x
Basic	x
Generalized Fairhurst	x
RocLab 1.0/ RocData 4.0	x	x
Residual Type
Absolute	x	x	x	x	x
Relative	x	x	x	x	x

LEVENBERG-MARQUARDT

The Levenberg-Marquardt method is a robust algorithm which has become a standard for non-linear regression. It is very reliable in practice, and has the ability to converge quickly from a wider range of initial guesses than other typical methods.

SIMPLEX

Users can also fit strength models to data using the Simplex method. The Simplex method is one of the best calibration methods, and has a reputation for being very reliable.

LINEAR REGRESSION

Linear Regression (linear least-squares) calibration is also available in RSData. It can only be used to fit the Hoek-Brown criterion for intact rock, and the Mohr-Coulomb strength model to lab data.

RESIDUALS

The Residuals value is a measure of how well a strength criterion fits a given data set. It is equal to the sum of the square of the distances of the given data points from the fitted curve. The “distance” depends on the method of error summation.

The goal of the calibration computation is to determine the strength envelope which minimizes the value of the Residuals. The Residuals value for the best fit strength envelope is displayed in the data legend.

Below is more description with respect to calibration methods with respect to Generalized Hoek-Brown criterion:

For generalized Hoek-Brown, when Linear Regression is used to find the strength envelope of best-fit, each triaxial data point must be transformed from the usual principal stress space to a linearized principal stress space, where the strength envelope becomes a linear function of the form of y = ax + b, where

• y = (sigma1 – sigma3)2
• x = sigma3
• a = mi * sigci
• b = sigci2

Parameters mi and sigci are derived from a and b, which are solved using Linear Regression. Note that the equation above is simply a rearrangement of the Generalized Hoek-Brown criterion for intact rock.

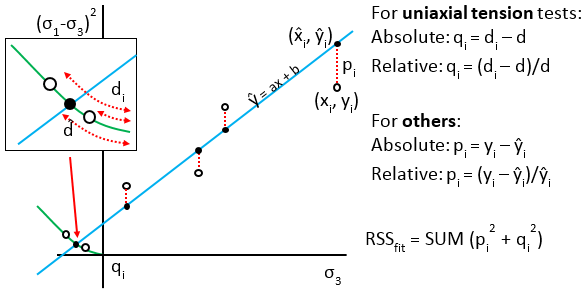
The curve of “best fit” is also determined by the method of error summation and the residual type. If error summation is vertical and the residual type is absolute, the solution is the familiar method of Least Squares, where the curve of best fit calculates error of the test data in the vertical direction to the curve. The error (also known as residual or RSS) is squared to prevent cancelling of positive and negative errors. This is shown in the following figure.

When the residual type is relative, the absolute residual is divided by the y-value of the curve fit. Using this type of residual normalizes the fit where errors may increase with larger values of sigma3.

The error summation type Parabolic Tensile is the same as vertical error summation except in the tensile region. This method is useful when Brazilian test data are available (sigma1 = 0), and these data points would fall on a parabola (y = x2) in the linearized principal stress space. The error for the tensile region then becomes the parabolic distance between the data point and where the parabola intersects the line of best fit. This is shown in the following figure.

MODIFIED CUCKOO

When using the Modified Cuckoo fitting algorithm, the user may calculate residuals either with the Basic or the Generalized Fairhurst methods.

Error summation in the Basic mode is illustrated below.

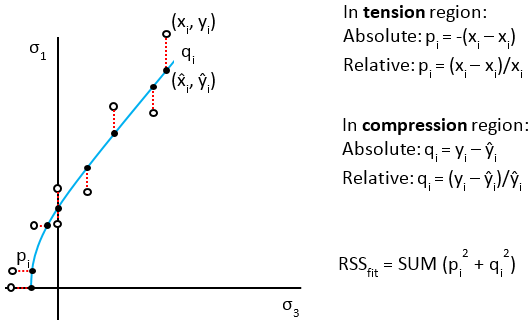
Residuals are calculated by the vertical distance to the curve of best fit for test data in the compression region (sigma3 >= 0) while they are calculated by the horizontal distance in the tension region (sigma3 < 0).

An extension to the Basic method of error summation is the Generalized Fairhurst. By inputting a sig1/sig3 ratio, the user can specify the transition point from the region of tension to the region of compression.

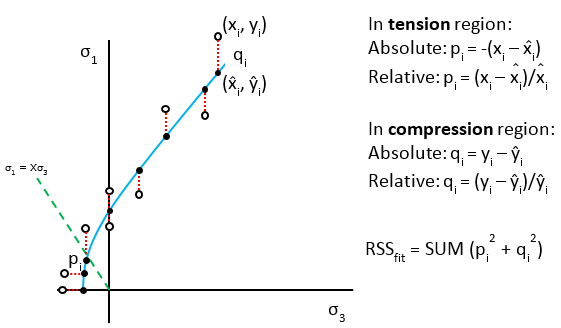
The ratio “X” (in σ1 = Xσ3) is the sig1/sig3 ratio and is based on concepts used in the Generalized Fairhurst equation (Fairhurst, 1964).

LEVENBERG-MARQUARDT OR SIMPLEX

For the Levenberg-Marquardt and Simplex fitting algorithms, errors are calculated using the Basic or RocLab 1.0/RocData 4.0 methods. The latter refers to the legacy error summation used in RocLab 1.0 and RocData 4.0. For this method, errors are calculated in the vertical direction except for the data points in the invalid tensile region, in which case data points are projected onto the inverted curve before errors are calculated vertically.