6 - Probabilstic Analysis
1.0 Introduction
In a Probabilistic Analysis, statistical input data can be entered to account for uncertainty in material unit weight, joint shear strength and joint water pressure. The result is a distribution of factors of safety, from which probability of failure is calculated for any given block formed from a single realization of the joint geometry (i.e., geometry of the blocks are deterministic across all sample runs; only material and joint property parameters are used as random variables).
Finished Product
The finished product of this tutorial can be found in the Tutorial 06 Probabilistic Analysis folder. All tutorial files installed with RocSlope3 can be accessed by selecting File > Recent Folders > Tutorials Folder from the RocSlope3 main menu.
2.0 Opening the Starting File
- Select File > Recent > Tutorials Folder.
- Go to the Tutorial 06 Probabilistic Analysis folder, and
open the file Tutorial 06 Probabilistic Analysis - starting file.rocslope_model.
This model already has the following defined and provides a good starting point to start computing blocks:
- External Geometry
- Measured Joints
In the starting model, Measured Joints are defined over the west extents of open pit.
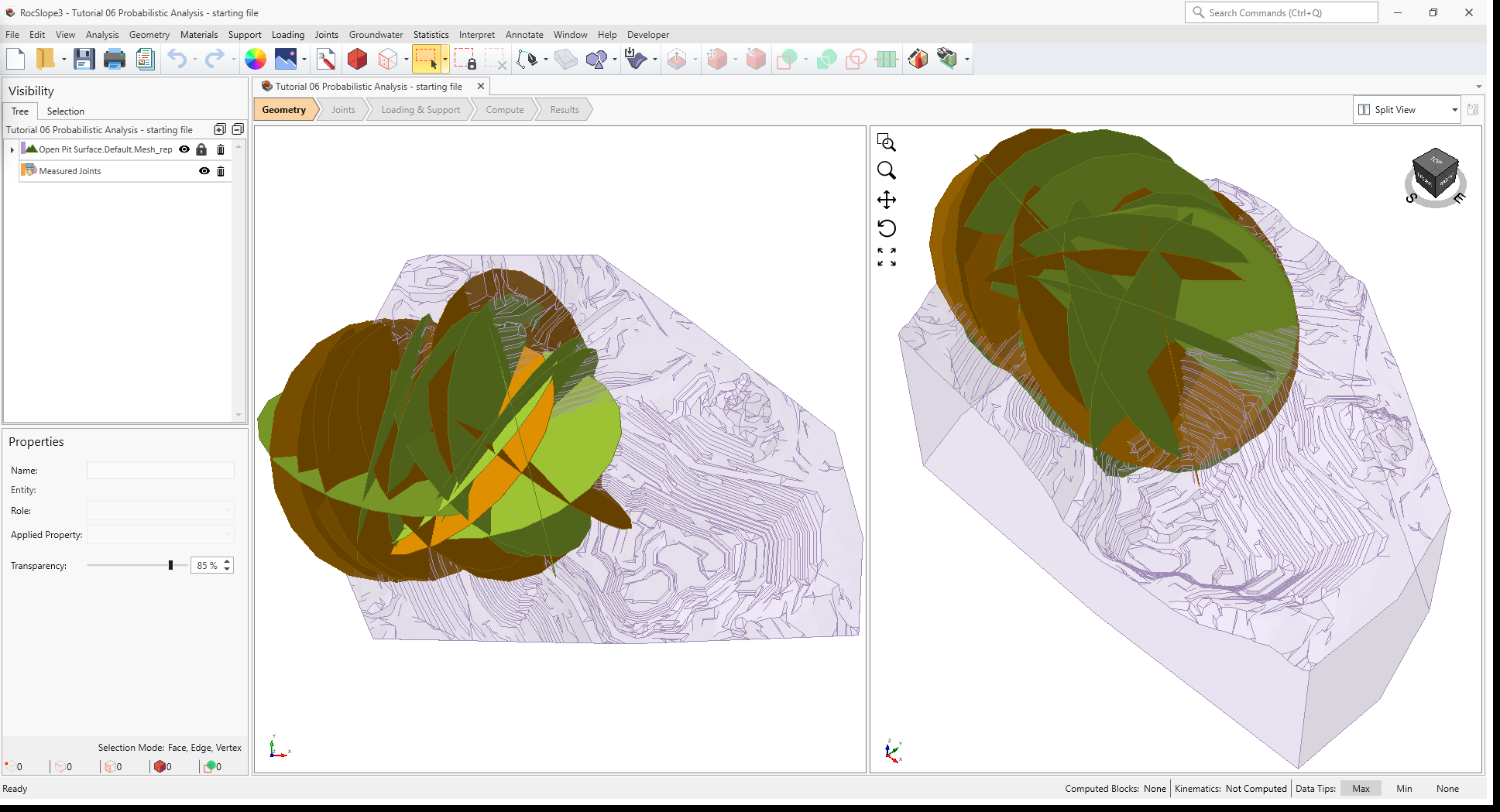
2.1 Project Settings
Our first step is to configure the Statistics settings for the model in Project
Settings.
- Select Analysis > Project Settings

- Select the Units tab. Ensure Units are Metric, stress as
MPa.
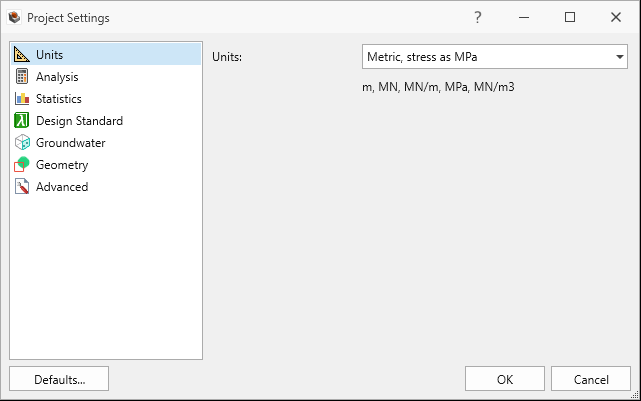
Units tab in Project Settings dialog - Select the Analysis tab.
- Set Design Factor of Safety = 1.5.
- Ensure Successive Failure is ON.
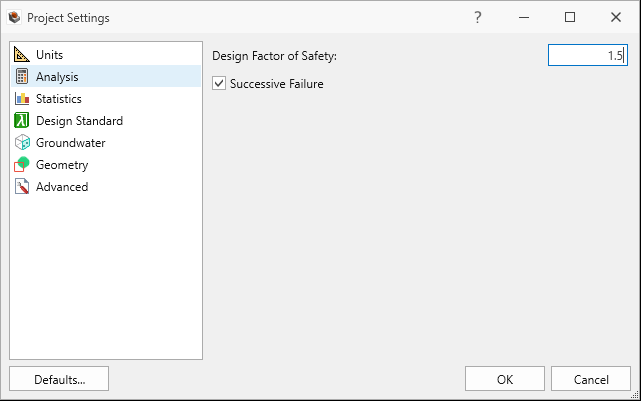
Analysis tab in Project Settings dialog
- Select the Statistics tab.
- Select Probabilistic Analysis to turn on probabilistic analysis mode.
- Leave the default Sampling Method = Latin-Hypercube and default Number of Samples = 1000
- Click OK to save the settings and close the dialog.
2.2 External Geometry
The External is of a pit shell and composed of one volume assigned with the Schist material
property. The Schist material property is currently defined as deterministic.
2.3 Measured Joints
Review the Measured Joints.
- Select Joints > Define Measured Joints

- Click Cancel to exit the dialog.
20 Measured Joints are defined are listed in order of Dip, Dip Direction, X, Y, Z, Radius, and Joint Property:
| Dip | Dip Direction | X | Y | Z | Radius | Joint Property |
|---|---|---|---|---|---|---|
| 59 | 48 | -390 | 1 | 1018 | 500 | Rough |
| 77 | 131 | -319 | 2 | 1004 | 500 | Rough |
| 78 | 123 | -313 | 4 | 1003 | 500 | Rough |
| 78 | 313 | -486 | 2 | 1037 | 500 | Rough |
| 61 | 13 | -793 | 4 | 1099 | 500 | Rough |
| 89 | 255 | -272 | -3 | 994 | 500 | Rough |
| 51 | 341 | -375 | -5 | 1015 | 500 | Rough |
| 67 | 107 | -548 | 47 | 1050 | 500 | Rough |
| 57 | 86 | -281 | 91 | 996 | 500 | Rough |
| 82 | 105 | -758 | 33 | 1092 | 500 | Rough |
| 53 | 62 | -546 | -1 | 1049 | 500 | Smooth |
| 46 | 84 | -665 | -2 | 1073 | 500 | Smooth |
| 55 | 79 | -772 | -4 | 1094 | 500 | Smooth |
| 29 | 90 | -798 | -4 | 1100 | 500 | Smooth |
| 50 | 82 | -305 | 193 | 1001 | 500 | Smooth |
| 34 | 83 | -699 | -5 | 1080 | 500 | Smooth |
| 39 | 87 | -348 | -3 | 1010 | 500 | Smooth |
| 81 | 36 | -258 | -5 | 992 | 500 | Smooth |
| 58 | 314 | -544 | -1 | 1049 | 500 | Smooth |
| 39 | 91 | -744 | -6 | 1089 | 500 | Smooth |
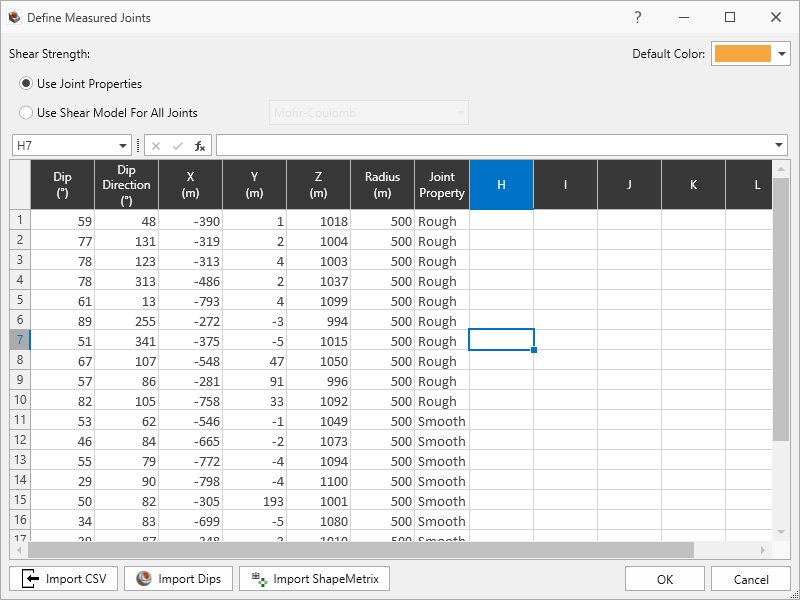
The Rough and Smooth joint properties are currently defined as deterministic.
3.0 Random Variables
In order to run a Probabilistic Analysis, at least one random variable must be defined and used in the model. In RocSlope3, the following can be set as a random variable:
- Material Property parameters (e.g., Unit Weight, Ru Value)
- Joint Property parameters (e.g., Cohesion, Phi, Waviness, Uniform Water Pressure)
For this model, we will be modelling the variability in unit weight of the material and the shear strength of the joints.
3.1 Material Property Statistics
To assign statistics to Material Properties:
- Select: Materials > Define Materials
 . The Define Materials dialog
shows the mean parameter values.
. The Define Materials dialog
shows the mean parameter values. - Select the Statistics
 button.
button. - Click the Add
 button.
button. - In the Add Random Variables dialog:
- Select Unit Weight (MN/m3).
- Click OK. The Unit Weight Property is added to the grid with a
Normal Distribution.
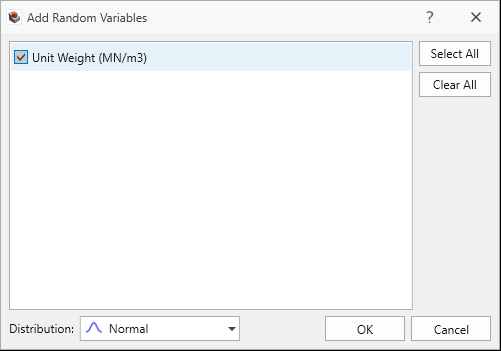
Add Random Variables dialog
- In order for the Unit Weight to be considered a valid random variable, a non-zero Standard Deviation, and
Relative Minimum and/or Relative Maximum must be set for the Schist Material Property's
Unit Weight:
- Distribution = Normal
- Mean = 0.026
- Std. Dev. = 0.002
- Rel. Min. = 0.005
- Rel. Max. = 0.005
The Rel. Min. and Rel. Max is relative to the Mean. They are not the absolute min and max values.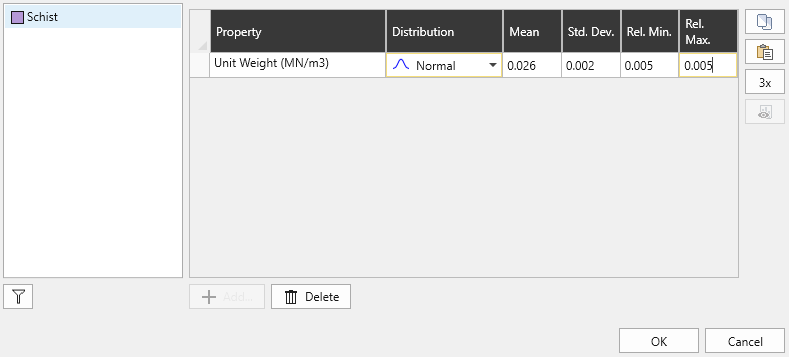
Define Material Statistics dialog - Click OK to close the Define Material Statistics dialog.
- Click OK again to close the Define Materials dialog.
The Define Material Statistics dialog allows users to add any applicable inputs as random variables. Only one Material Property exists (i.e., Schist).
The Define
Material Statistics dialog can also be accessed in Statistics > Define Material
Statistics 
3.2 Joint Property Statistics
To assign statistics to Joint Properties:
- Select Joints > Define Joint Properties
 . The Define Joint Properties dialog shows
the mean parameter values.
. The Define Joint Properties dialog shows
the mean parameter values. - Click the Statistics
 button.
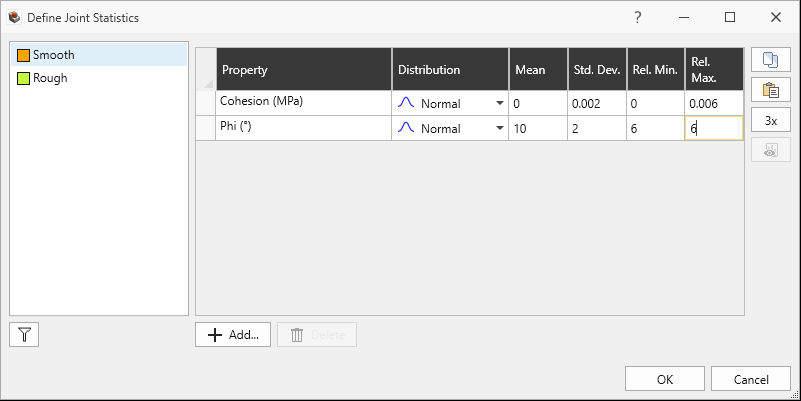
button. - For the Smooth Joint Property:
- Click the Add
 button.
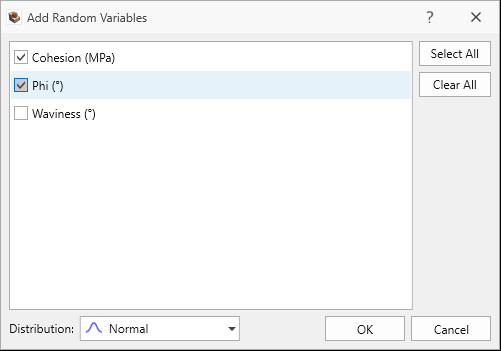
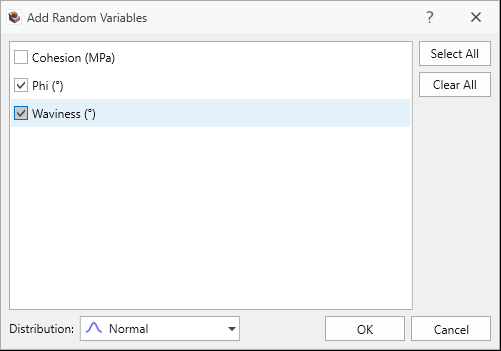
button. - In the Add Random Variables dialog:
- Select Phi and Cohesion.
- Click OK. The Cohesion and Phi properties are added to the grid with a Normal Distribution.
- For Cohesion:
- Distribution = Normal
- Mean = 0
- Std. Dev. = 0.002
- Rel. Min. = 0
- Rel. Max. = 0.006
- For Phi:
- Distribution = Normal
- Mean = 10
- Std. Dev. = 2
- Rel. Min. = 6
- Rel. Max. = 6
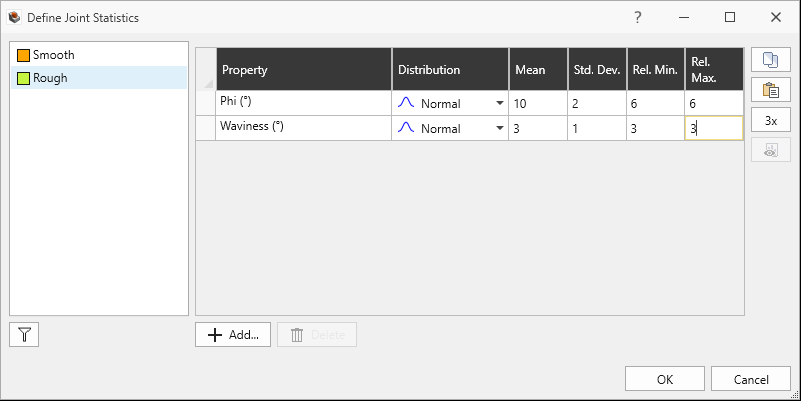
- For the Rough Joint Property:
- Select the Add
 button.
button. - In the Add Random Variables dialog:
- Select Phi and Waviness.
- Click OK. The Phi and Waviness properties are added to the grid with a Normal Distribution.
- For Phi:
- Distribution = Normal
- Mean = 10
- Std. Dev. = 2
- Rel. Min. = 6
- Rel. Max. = 6
- For Waviness:
- Distribution = Normal
- Mean = 3
- Std. Dev. = 1
- Rel. Min. = 3
- Rel. Max. = 3
- Click OK to close the Define Joint Statistics dialog.
- Click OK again to close the Define Joint Properties dialog.
The Define Joint Property Statistics dialog allows users to add any applicable inputs as random variables. There are two Joint Properties.
The Define Joint Statistics
dialog can also be accessed in Statistics > Define Joint Property Statistics 
4.0 Compute
RocSlope3 has a two-part compute process.
4.1 Compute Blocks
The first step is to compute the blocks which may potentially be formed by the intersection of joints with other joints and the intersection of joints with the free surface.
To compute the blocks:
- Navigate to the Compute workflow tab

- Select Analysis > Compute Blocks

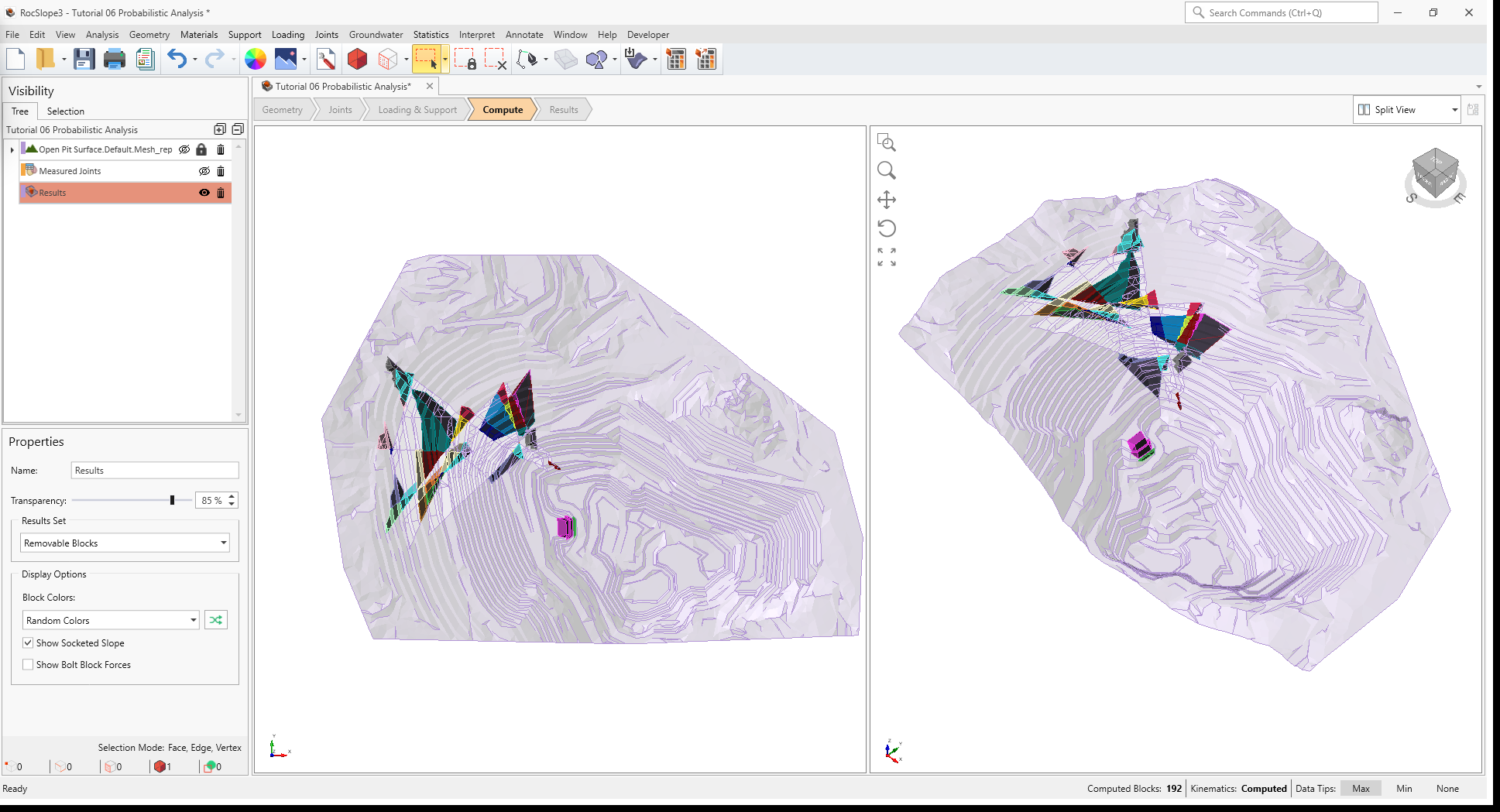
As compute is run, the progress bar reports the compute status. Once compute is finished, the Results node is added to the Visibility Tree and All Valid Blocks are blocks are shown in the viewport. The Results node consists of the collection of valid blocks and the socketed slope. The original External and Measured Joints visibility is turned off.
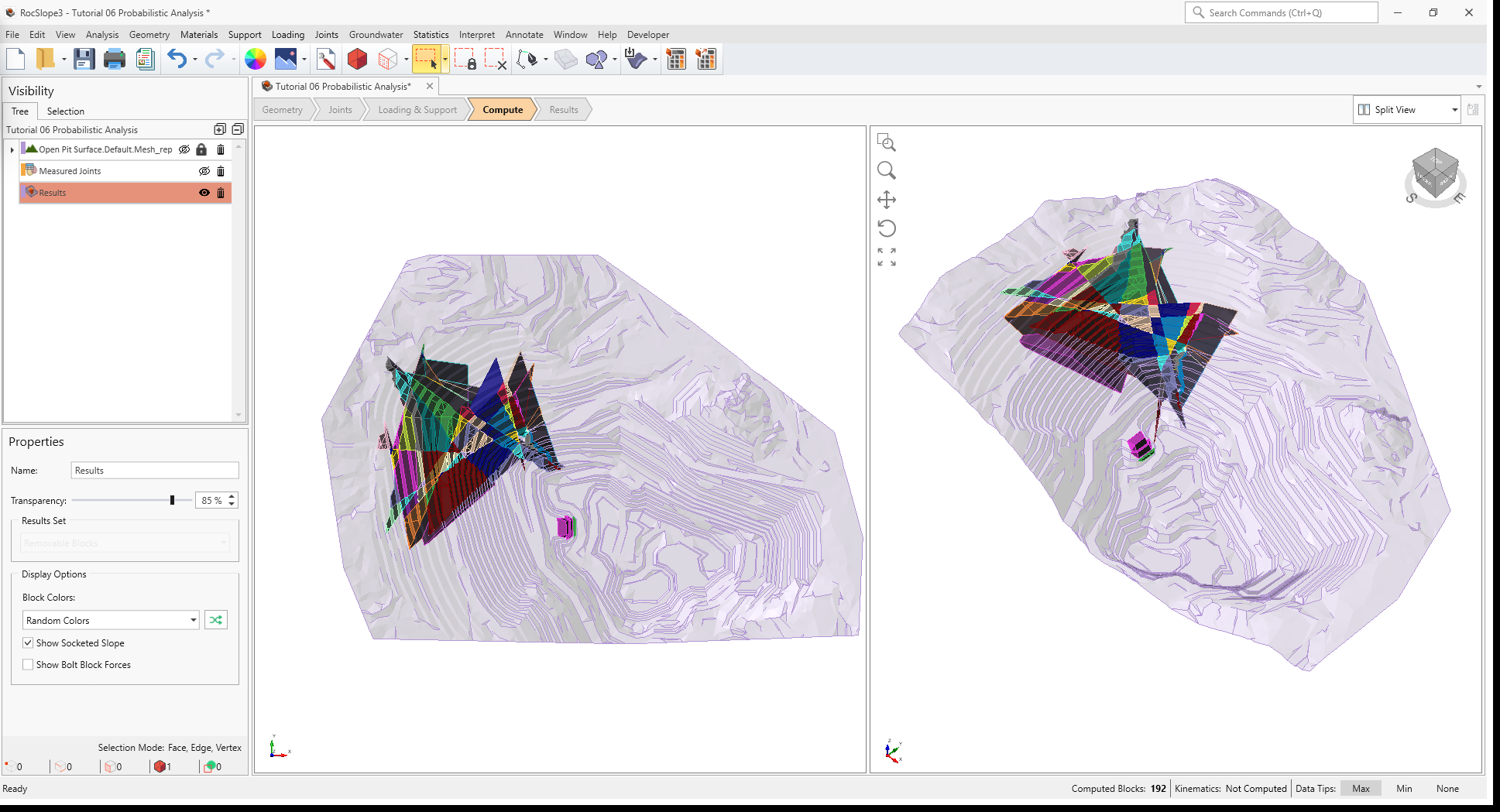
Once compute is finished, the blocks are coloured according to the Block Color option (Random
Colors) set in the Results node's Property pane.
Compute Blocks only determines the geometry of the blocks. In order to obtain other information such as the factor of safety, Compute Kinematics needs to be run.
4.2 Compute Kinematics
The second and final compute step is to compute the removability, forces, and factor of safety for each of the valid blocks.
To compute the block kinematics:
- Ensure that the Compute workflow tab
 is the active workflow.
is the active workflow. - Select Analysis > Compute Kinematics

As compute is run, the progress bar reports the compute status. By default, after Compute Kinematics is run, only Removable Blocks are shown.
In this Probabilistic Analysis, for each block, the kinematics are computed 1,000 times, each time with statistically sampled inputs for Unit Weight of the Schist Material Property, Cohesion and Phi for the Smooth Joint Property, and Phi and Waviness for the Rough Joint Property, according to their respective random variables' distributions.
5.0 Interpreting Results
Since block geometry does not change between probabilistic runs (i.e., deterministic joint geometry), the
visualization of the Results in the 3D CAD View is representative of all possible block geometries.
Once both blocks and kinematics are computed, all block results can be viewed in a grid format.
5.1 Block Information
To view all block results:
- Navigate to the Results workflow tab

- Select Interpret > Block Information

Visualizing blocks can be difficult when the slope extents are large compared to the block extents.
To zoom into all blocks:
- Select Interpret > Zoom To All Blocks

The Block Information pane shows the collection of blocks according to the Results Set
settings. The Results Set shown can be selected in the Results tab of the Display Options, or the Properties pane for the Results Node. In this case, only Removable
Blocks are coloured and listed in Block Information.
In the case of a Probabilistic Analysis, for any given block, the Factors of Safety are affected by the random variables being sampled in each run. This then affects which blocks are considered "Failed" (i.e., Factor of Safety < Design Factor of Safety). In the case of Successive Removal, this also impacts the Removability of blocks which can only be removed if key blocks are removed. For these reasons, the definitions of the Results Set displayed are modified for a Probabilistic Analysis as follows:
- All Valid Blocks: Identical as Deterministic Analysis since block formation is independent of the random variables for material and joint properties.
- Removable Blocks: For a given block, if any sample run results in the block being Removable, then the block is included in the Results Set.
- Failed Blocks (FS < Design FS): For a given block, if any sample run results in the Factor of Safety < Design Factor of Safety, then the block is included in the Results Set.
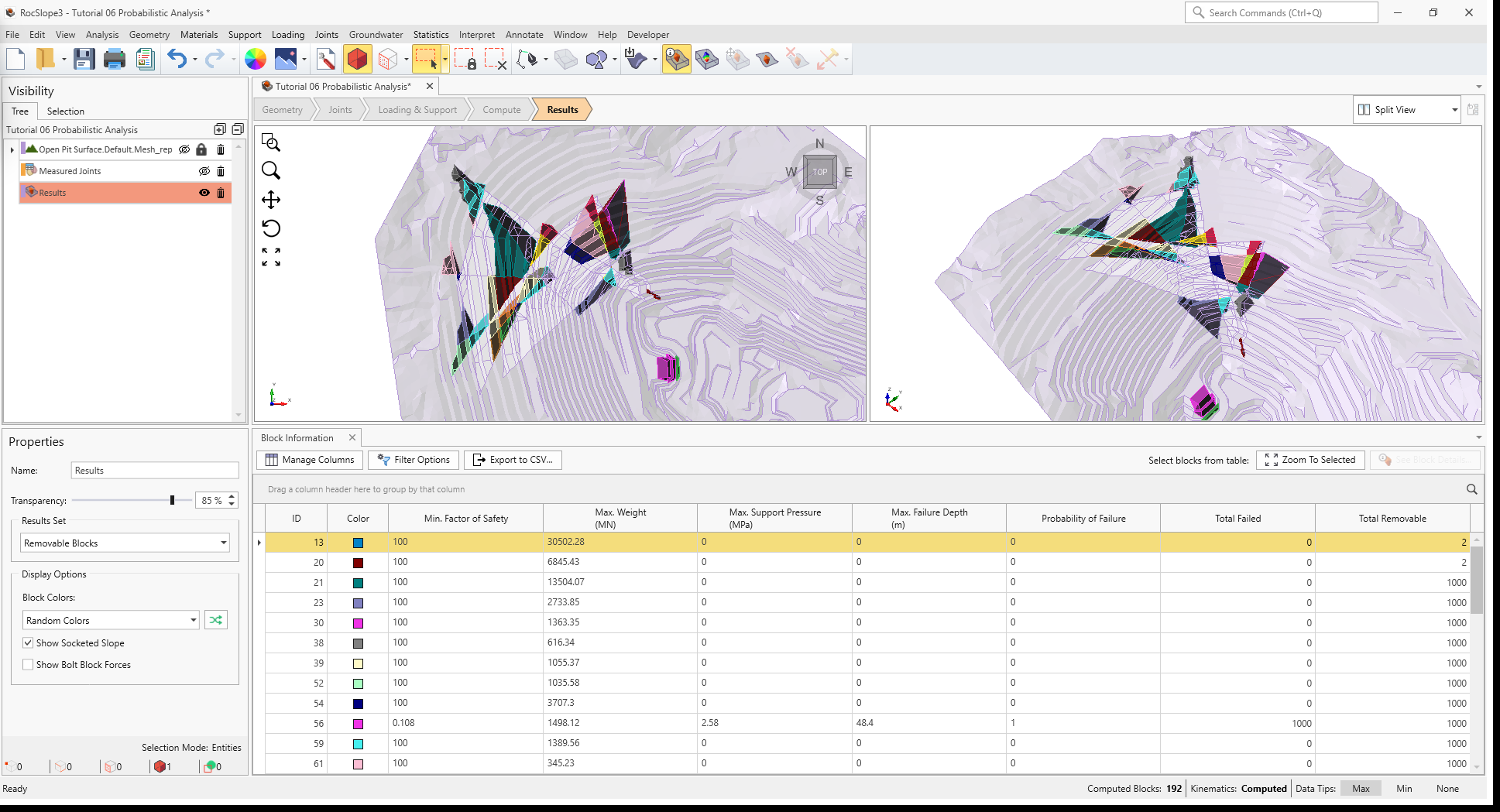
For Probabilistic Results, only the critical values among all sample runs are reported for each block:
- Minimum Factor of Safety
- Maximum Weight
- Maximum Required Support Pressure
- Maximum Failure Depth
- Probability of Failure
- Total Removable
- Total Failed
5.2 Contour Blocks
In RocSlope3, blocks can be contoured by several metrics. In a Probabilistic Analysis, blocks can be contoured by any of the critical values.
To show block contours:
- Select Interpret > Contour Blocks

- From the Legend pane to the right, select Probability of Failure. The blocks
are contoured by the Probability of Failure = Total Failed / Number of Samples.
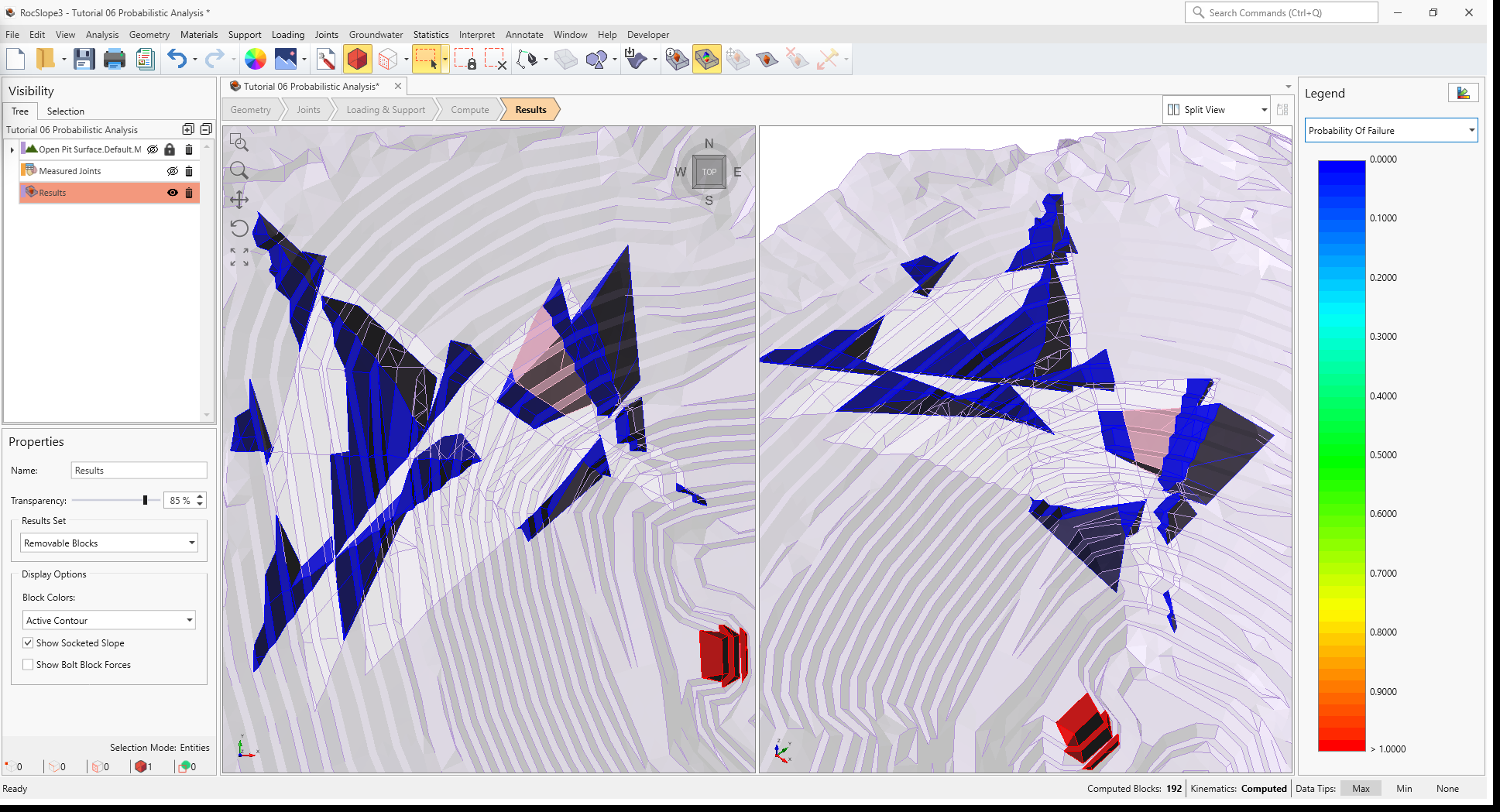
3D View of Removable Blocks contoured by Probability of Failure - From the Legend pane to the right, select Max. Support Pressure.
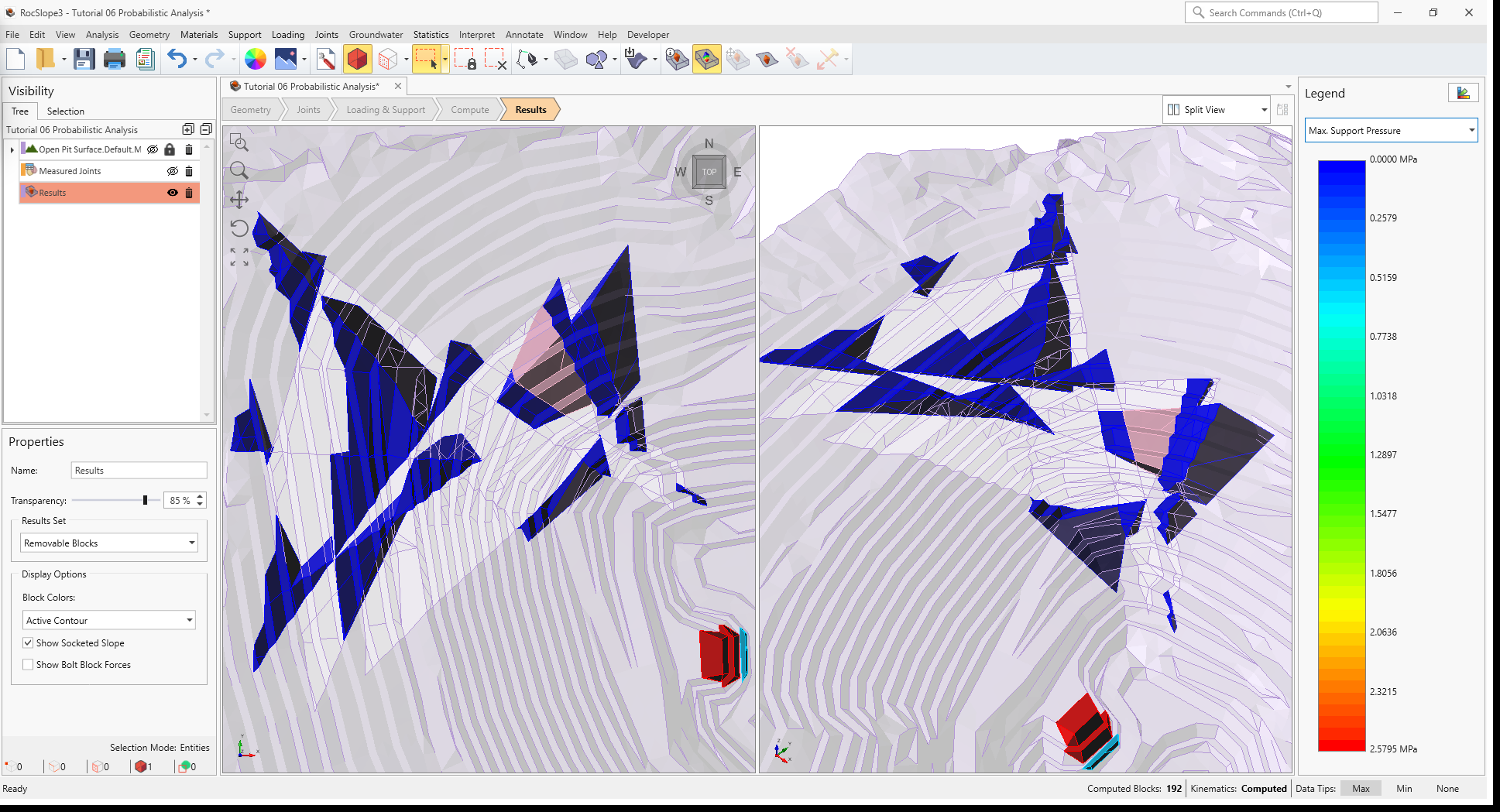
3D View of Removable Blocks contoured by Max. Support Pressure
Note that probabilistic results, like deterministic results, are location-specific.
6.0 Statistical Plots
Input or output distributions can be charted in the following forms:
- Histogram Plot
- Scatter Plot
- Cumulative Plot
For each type of plot, the blocks considered in the plot data can be one of the three:
- Current Result Set (blocks considered in All Valid Blocks, Removable Blocks, or Failed Blocks, as selected in
Display Options)
- Single Block (a single block is considered, identified by Block ID)
- Filtered Blocks
6.1 Histogram Plot
Histogram Plots allow users to see the ordered frequency of a set of block data.
To plot a histogram plot:
- Select Statistics > Histogram Plot
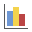
- In the Histogram Plot dialog:
- Set Data to Plot = Factor of Safety
- Set Number of Bins = 30
- Set Blocks to Plot = Single Block and Block ID = 56
- Select the Highlight Data checkbox and set the Factor of Safety < 1.5 to highlight any values less than the Design Factor of Safety.
- Select the Best Fit Distribution checkbox to plot the fitted distribution
- Select Relative Frequency to scale the histogram Frequency axis such
that the area under then distribution = 1. Otherwise, the Frequency is simply the count.
Histogram Plot dialog - Click Plot to generate the histogram.
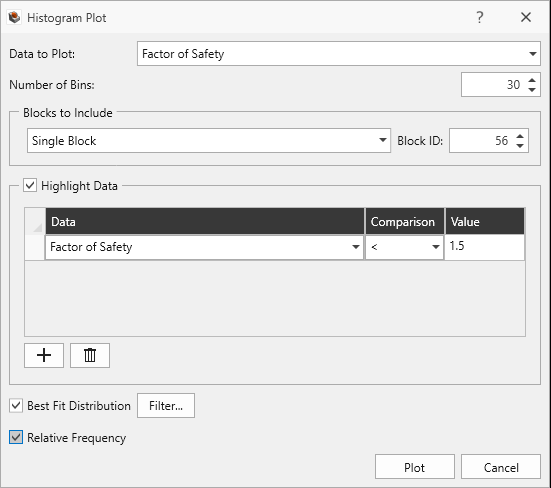
- Set Data to Plot = Factor of Safety
Relative Frequency is plotted on the y-axis, while Factor of Safety is plotted on the x-axis, lumped into 30 bins. The Best Fit Distribution shows the distribution type and parameters which best fit the data. The highlighted bars indicate the Relative Frequency of Factor of Safety < 1.5 (blocks which are kinetically unstable); all sample runs for this block results in a Factors of Safety < 1.5.
6.2 Scatter Plot
Scatter Plots allow users to see the correlation between two sets of block data.
To plot a scatter plot:
- Navigate back to the 3D Geometry View by selecting the tab below the toolbar at the top of the screen.
- Select Statistics > Scatter Plot

- In the Scatter Plot dialog:
- Set Horizontal Axis = Factor of Safety
- Set Vertical Axis = Smooth: Phi
- Set Blocks to Plot = Single Block and Block ID = 56
- Select the Highlight Data checkbox and set the Factor of Safety < 1.5 to highlight any values less than the Design Factor of Safety.
- Select the Regression Line checkbox to plot the line of best fit.
- Click Plot to generate the scatter plot.
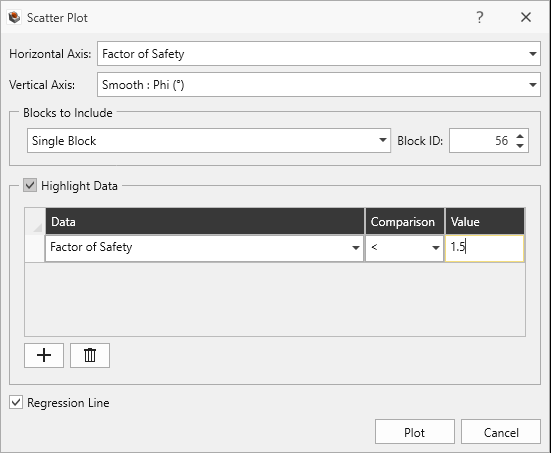
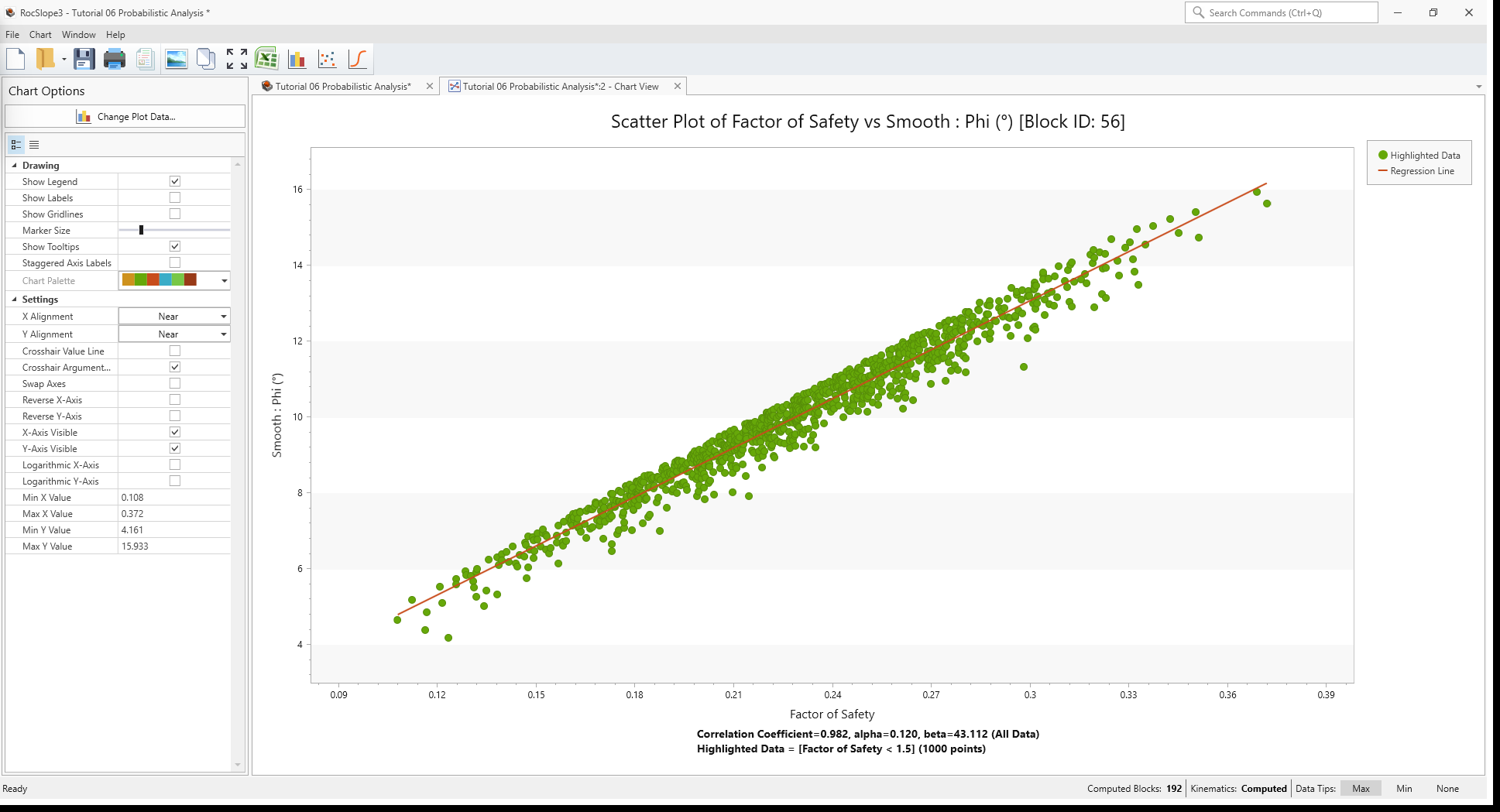
The Regression Line and tight clustering of the scatter plot data points around that line indicates that there is a strong correlation between Factor of Safety and Friction Angle of the Smooth joint property.
6.3 Cumulative Plot
Cumulative Plots allow users to see the cumulative probability of a set of block data.
To plot a cumulative plot:
- Navigate back to the 3D Geometry View by selecting the tab below the toolbar at the top of the screen.
- Select Statistics > Cumulative Plot
- In the Cumulative Plot dialog:
- Set Data to Plot = Weight
- Set Number of Bins = 30
- Set Blocks to Plot = Current Result Set
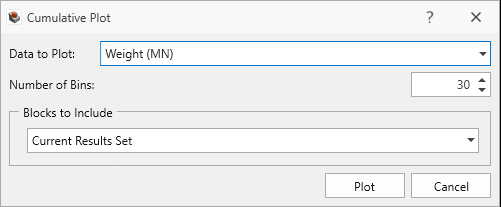
Cumulative Plot dialog - Click Plot to generate the cumulative plot.
- Set Data to Plot = Weight
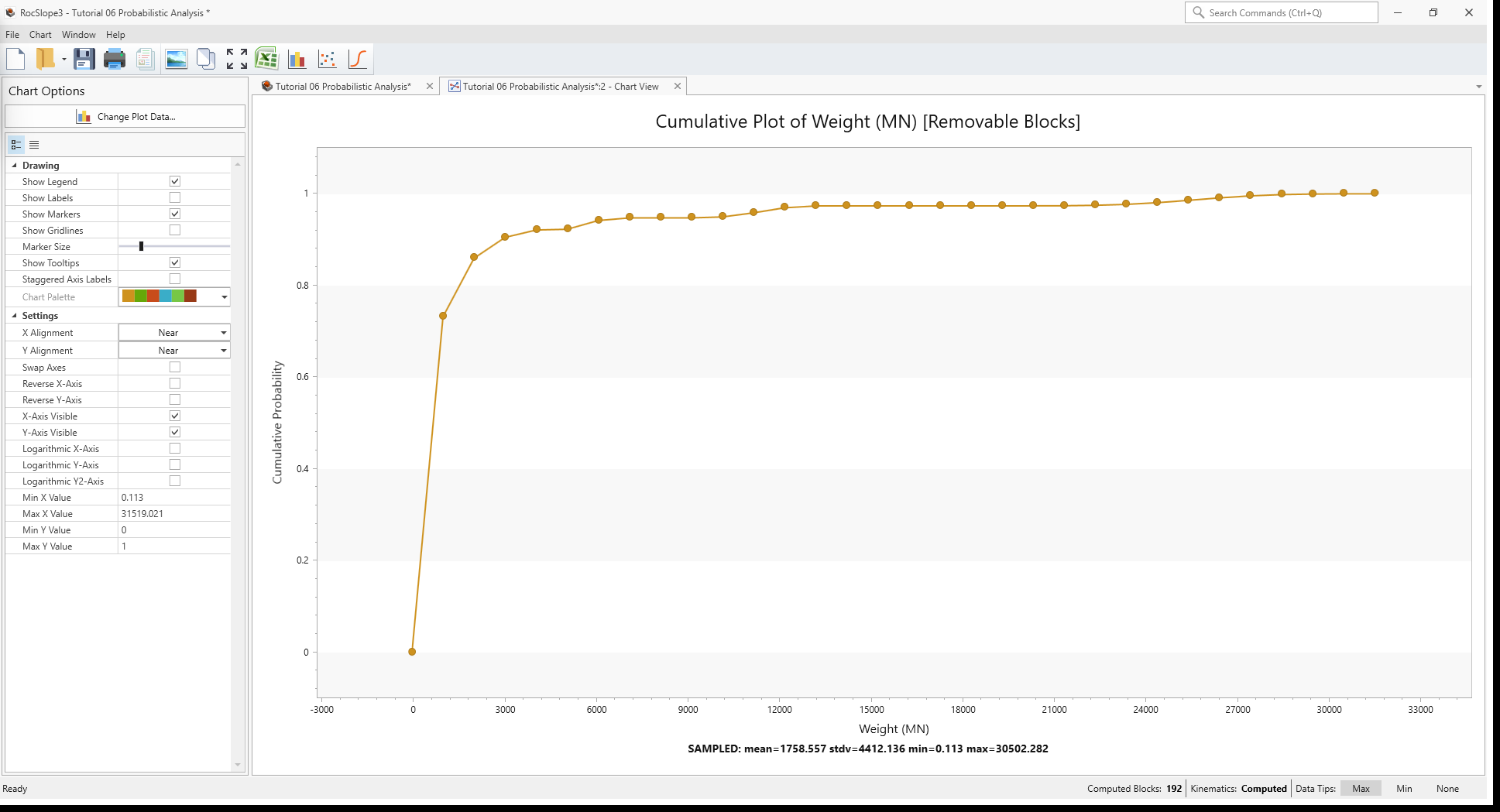
The cumulative plot shows the cumulative distribution of block Weight values for the Removable Results Set. At any given Weight value, the Cumulative Probability is the percentile (as a fraction) of blocks sampled which have a Weight less than or equal to that value. Vice versa, looking at some percentile we can get the corresponding Weight value (e.g., 90th percentile would correspond to approx. Weight = 3000 MN).
This concludes Tutorial 06.