2 - Probabilistic Analysis
1.0 Introduction
This tutorial will familiarize you with the Probabilistic analysis features of RocTopple. In a Probabilistic analysis, you can define statistical distributions for input parameters (e.g., slope geometry, shear strength, water level) to account for uncertainty in their values. When the analysis is computed, the result is a distribution of Factors of Safety, from which a Probability of Failure is calculated.
Topics Covered in this Tutorial:
- Project Settings
- Random Variables
- Mean Slope
- Histograms
- Scatter Plots
- Cumulative Plots
- Info Viewer
Finished Product:
The finished product of this tutorial can be found in the Tutorial 2 Probabilistic Analysis.rtop file, located in the Examples > Tutorials folder in your RocTopple installation folder.
2.0 Creating a New File
- Start RocTopple by selecting Programs > Rocscience > RocTopple > RocTopple from the Windows Start menu.
RocTopple automatically opens a new blank document, which allows you to begin creating a model immediately. If the RocTopple application window is not already maximized, maximize it now so the full screen space is available for use.
If you do NOT see a model on your screen:
- Select: File > New

Whenever a new file is created, the default input data will form valid slope geometry, as shown in the figure below:
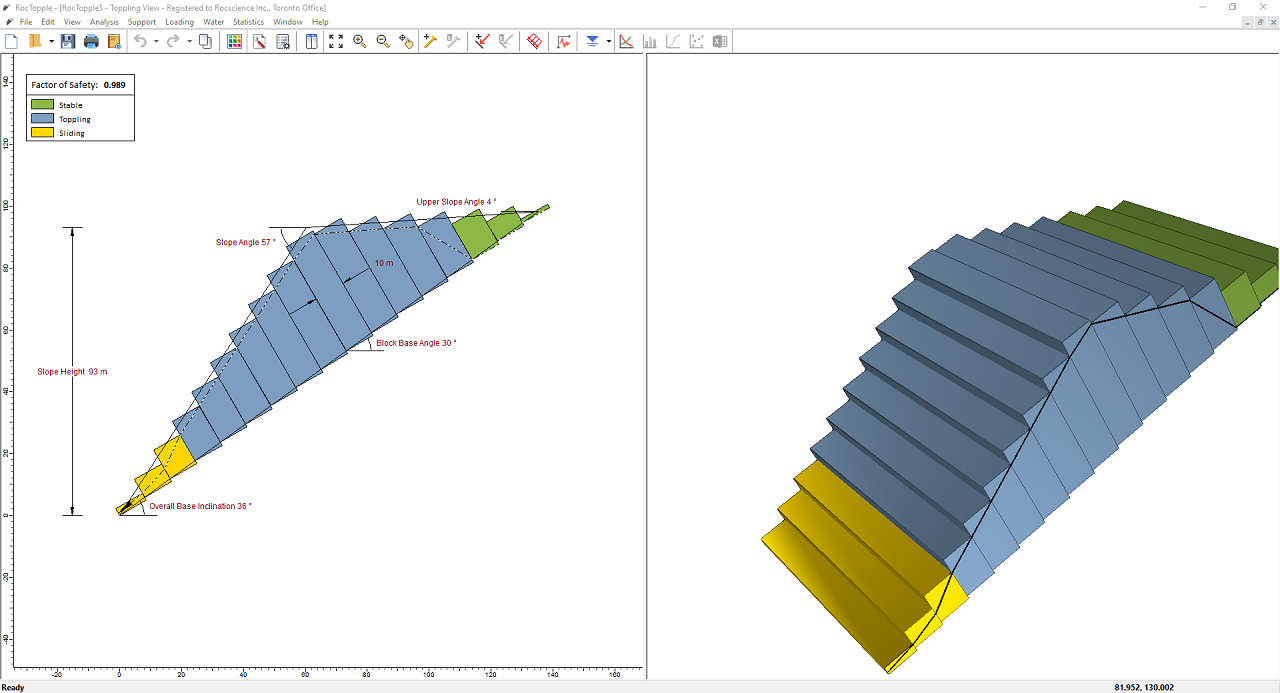
Notice the split screen format of the display. The 2D View shows the slope geometry and the factor of safety, while the 3D View is interactive. Note that the computation is for two-dimensional geometry and assumes unit depth.
3.0 Project Settings
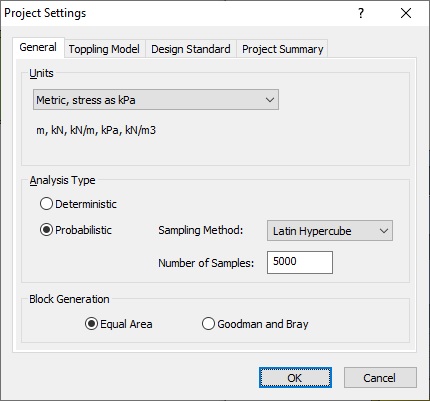
The Project Settings dialog allows you to configure the main analysis parameters for your model (i.e., Analysis Type, Units, Sampling Method, etc.). To open the dialog:
- Select: Analysis > Project Settings

3.1 UNITS
For this tutorial we will be using the Metric units, stress as kPa.
3.2 ANALYSIS TYPE
- In the General tab, change the Analysis Type to Probabilistic.
3.3 SAMPLING AND RANDOM NUMBERS
The Sampling Method determines how statistical distributions for the random input variables will be sampled. The default Sampling Method is Latin Hypercube and the default Number of Samples is 5,000. See Sampling Method Setting in RocTopple for more information about the sampling options.
- Do not make any changes to these settings. We will use the defaults.
3.4 TOPPLING MODEL
There are two main Toppling Models in RocTopple: Block Toppling and Block Flexure Toppling.
- For this tutorial we will use the Block Toppling model, which is the default setting.
3.5 PROJECT SUMMARY
- Select the Project Summary tab in the Project Settings dialog.
- Enter RocTopple Probabilistic Analysis Tutorial as the Project Title.
NOTES:
- The Project Summary information can be displayed on printouts of analysis results using the Page Setup option in the File menu and defining a Header and/or Footer.
- You can specify the Author and Company in the dialog so that this information always appears by default in the Project Summary for new files.
- Click OK to save settings and close the Project Settings dialog.
The legend in the upper-left corner of the 2D View should say Probability of Failure: Not Computed. This is because RocTopple currently has the Autocompute feature turned off so, to get results, you must manually click Compute on the Analysis menu.
But don't click Compute just yet. We need to define random variables first.
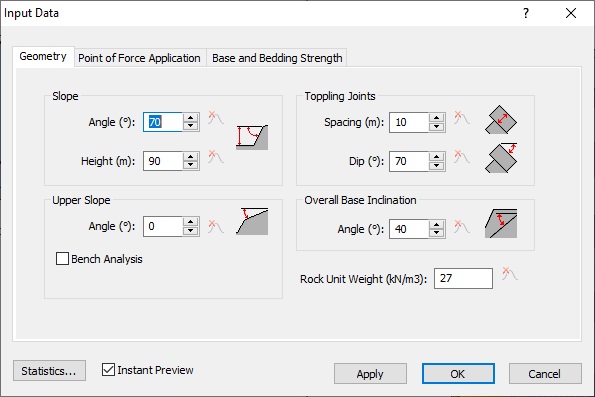
4.0 Probabilistic Input Data
Next we'll define some random variables for our Probabilistic analysis, using the Input Data dialog. To open the dialog:
- Select: Analysis > Input Data

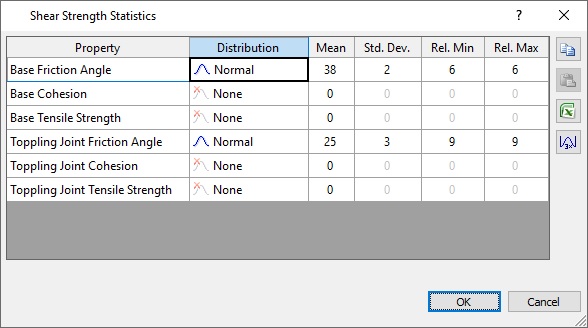
Random variables can be defined using the Quick-Stats button  next to the individual parameter or using the Statistics button at the bottom-left corner of the dialog.
next to the individual parameter or using the Statistics button at the bottom-left corner of the dialog.
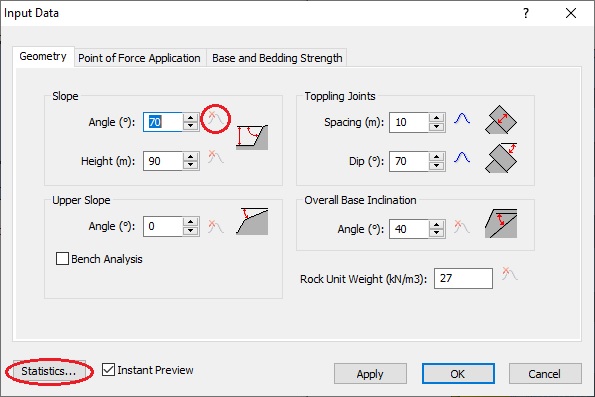
To carry out a Probabilistic analysis with RocTopple, at least one input parameter must be defined as a random variable. To define an input parameter as a random variable, select a statistical distribution for the variable (e.g., Normal, Uniform, etc.) and enter the required statistical parameters (e.g., mean, standard deviation, minimum and maximum values).
For this example, we will define the following input parameters as random variables:
- Toppling Joints Spacing
- Toppling Joints Dip
- Base Joints Shear Strength Friction Angle
- Toppling Joints Shear Strength Friction Angle
All other input parameters will be assumed to be “exactly” known (i.e., Statistical Distribution = None) and will not be involved in the statistical sampling.
4.1 GEOMETRY
Let's start by defining Toppling Joints Spacing and Toppling Joints Dip as random variables.
- Select the Geometry tab in the Input Data dialog.
- Enter the following data for the different geometric parameters.
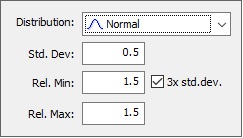
These values are the mean values for random variables and the exact known values for variables without a statistical distribution. - Click the Quick-Stats button
 next to Toppling Joints Spacing and enter the following statistical data in the Distribution popup:
next to Toppling Joints Spacing and enter the following statistical data in the Distribution popup: - Distribution = Normal
- Std. Dev = 0.5
- Click OK to close the Distribution popup.
Notice that the Quick-Stats button icon has changed to show a Normal distribution. You can mouse over the button to display a tooltip with your input. - Click the Quick-Stats button
 next to Toppling Joints Dip and enter the following statistical data in the Distribution popup:
next to Toppling Joints Dip and enter the following statistical data in the Distribution popup: - Distribution = Normal
- Std. Dev =: 5
- Click OK to close the Distribution popup.
Slope Angle | 70° |
Slope Height | 90m |
Upper Slope Angle | 0° |
Toppling Joints Spacing | 10m |
Toppling Joints Dip | 70° |
Overall Base Inclination | 40° |
Rock Unit Weight | 27 kN/m3 |
The 3x std. dev check box is selected by default, so the Rel. Min and Rel. Max values are automatically calculated.
TIP: You can view a summary of the random variables in the Geometry Statistics dialog by clicking the Statistics button at the bottom-left corner of the tab. You can also use this dialog to input values for several variables at once.
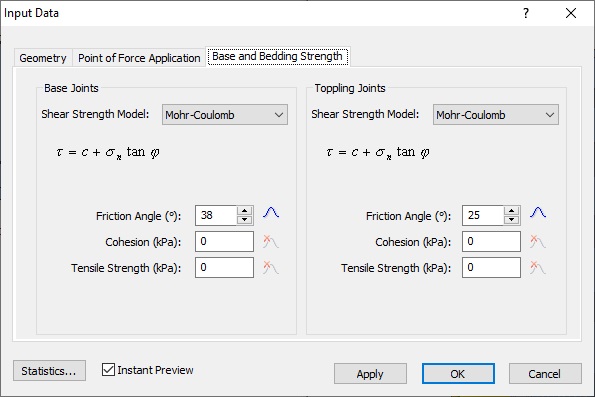
4.2 BASE AND BEDDING STRENGTH
Next, we'll define Base Joints Shear Strength Friction Angle and Toppling Joints Shear Strength Friction Angle.
- Select the Base and Bedding Strength tab in the Input Data dialog.
- Select Mohr-Coulomb as the Shear Strength Model for both Base Joints and Toppling Joints.
- Set Base Joints Friction Angle = 38 and click the corresponding Quick-Stats button
 .
. - In the Distribution popup, set Distribution = Normal and Std. Dev = 2, and click OK.
- Set Toppling Joints Friction Angle = 25 and click the corresponding Quick-Stats button
 .
. - In the Distribution popup, set Distribution = Normal and Std. Dev = 3, and click OK.
- Click OK in the Input Data dialog to submit the values and close the dialog.
TIP: As in the Geometry tab, you can click the Statistics button on the left-bottom corner to open the Shear Strength Statistics dialog to view or edit variable values.
5.0 Compute
We are now ready to run the Probabilistic analysis.
- Click Compute
 to run the RocTopple Probabilistic analysis.
to run the RocTopple Probabilistic analysis.
The progress of the calculation is indicated in the Compute Samples dialog.
Using the Latin Hypercube sampling method, RocTopple generates 5,000 random input data samples for each random variable using the specified statistical distributions. Likewise, it computes the Factor of Safety for 5,000 possible slopes.
Note that the Autocompute option is currently turned off, which is why we had to manually select Compute to get results. You can enable Autocompute by selecting Autocompute on the Analysis menu and selecting the Autocompute for probability analysis check box in the Autocompute popup dialog.
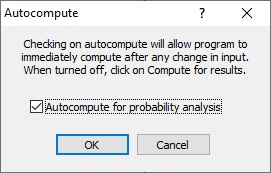
Turning on Autocompute results in the re-sampling of random variables and the re-calculation of results each time an input is changed. Since this is not recommended for calculating a large number of samples, we'll leave the option OFF for this tutorial.
6.0 Probabilistic Analysis Results
The primary result of interest from a Probabilistic analysis is the Probability of Failure, which is displayed in the legend in the top-left corner of the 2D View. For this tutorial, you should obtain a Probability of Failure of 0.91 or 91%, as shown in the figure below.

TIP: To change the number of decimals displayed for the Probability of Failure, right-click on the 2-D view, select Display Options, change FS Significant Digits to the desired number, click Apply, and click Close.
6.1 INFO VIEWER
A summary of the analysis results is displayed in the Info Viewer. To access the Info Viewer:
- Select: Analysis > Info Viewer

Under the section Probabilistic Analysis Results, you should see the following:

The results show that, for 5000 samples, all samples had valid geometry (Number of Valid Computations = 5000). Out of the Number of valid Computations, 4552 samples failed (Factor of Safety < 1), while 448 samples are safe (Factor of Safety >= 1). Note that these two values should add up to the Number of Valid Computations.
The Probability of Failure is equal to the Number of Failed Slopes divided by the Number of Valid Computations (4552/5000 = 0.91).
The Probability of Failure for Converged Samples is equal to the Number of Failed Slopes divided by the number of samples for which a safety factor was found. In this case, all 5000 samples converged, so the Probability of Failure for Converged Samples is equal to the Probability of Failure.
6.2 HISTOGRAMS
You can plot a histogram of results using the Plot Histogram dialog.
- Select Plot Histogram
 on the toolbar or the Statistics menu.
on the toolbar or the Statistics menu.
The Data to Plot is set to Factor of Safety by default. - Leave Number of Bins = 30.
- Select the Highlight Data check box and leave the Factor of Safety to <1.
- Click Plot.
A histogram of the Factor of Safety is displayed in the Histogram View.
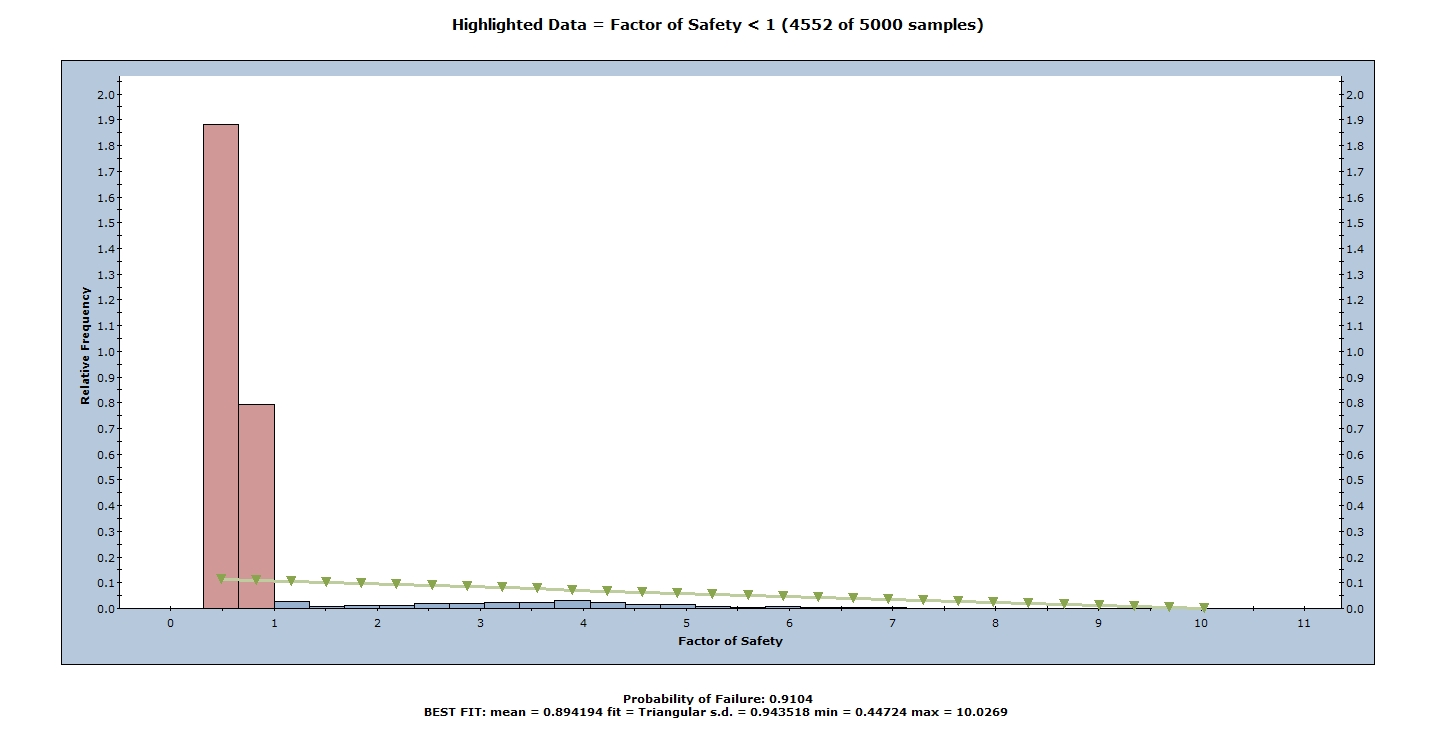
The histogram represents the distribution of the Factor of Safety for all valid slopes generated by the random sampling of the input data. The red bars to the left represent slopes with a Factor of Safety of less than 1.0. The green line is a best-fit to the Factor of Safety distribution.
6.2.1 Mean Factor of Safety
At the bottom of the histogram plot, notice the mean, fit, standard deviation, and minimum and maximum values of the Factor of Safety distribution. Note that the mean Factor of Safety from a Probabilistic analysis (i.e., the average of all of the Factors of Safety generated by the analysis) is in general different from the Factor of Safety of the Mean Slope (i.e., the Factor of Safety of the slope corresponding to the mean input data values). In this case:
- From the histogram, the mean Factor of Safety = 0.894.
- The Factor of Safety of the Mean Slope = 0.624 (if you were to change to a Deterministic analysis).
Theoretically, for an infinite number of samples, these two values should be equal. However, due to the random nature of the statistical sampling, the two values are usually different for a typical Probabilistic analysis with a finite number of samples.
6.2.2 Histograms of Other Data
In addition to the Factor of Safety, you can plot histograms of random input variables (i.e., any input data variable that was assigned a statistical distribution).
- Select Plot Histogram
 on the toolbar or the Statistics menu.
on the toolbar or the Statistics menu. - In the Histogram Plot dialog, select Toppling Joint Spacing in the Data to Plot drop-down.
- Click OK.
A histogram of the Toppling Joint Spacing and the input data distribution is displayed.
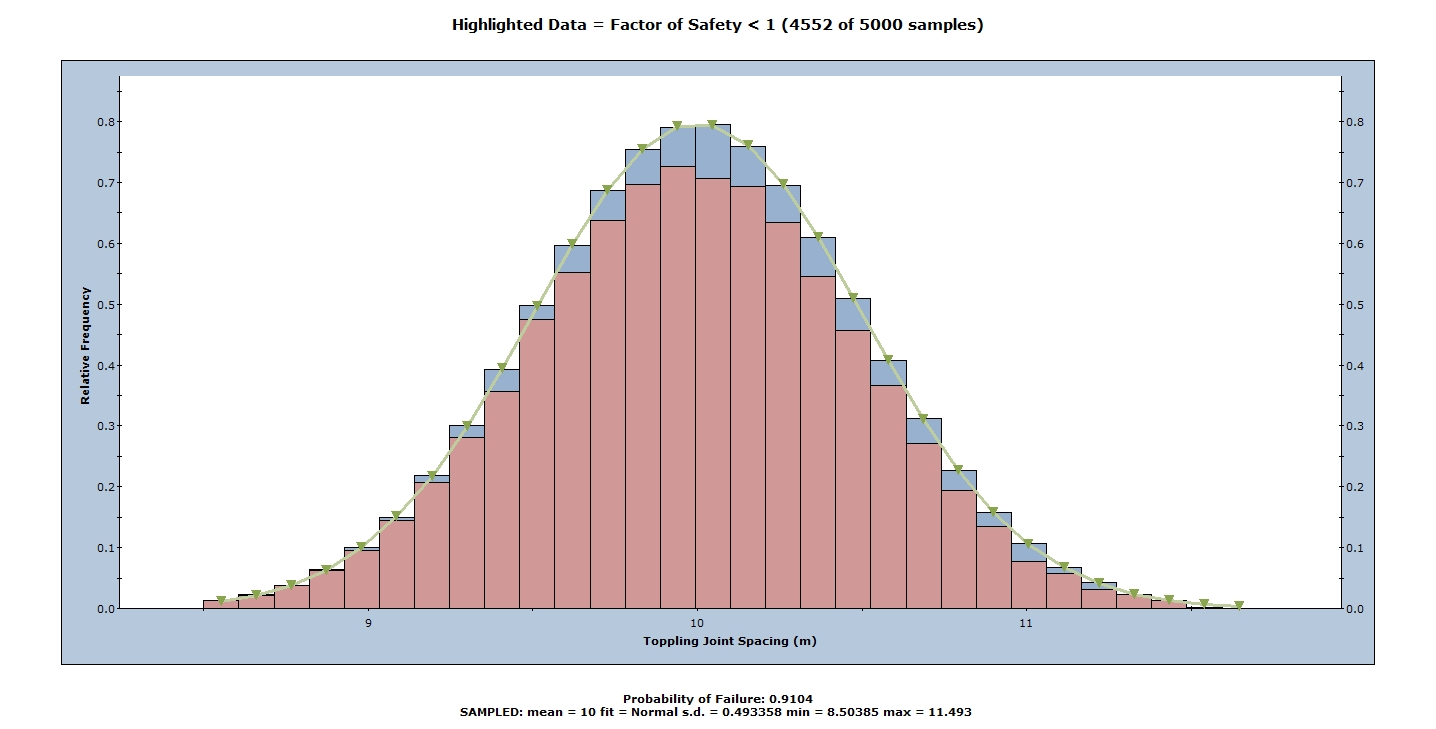
In this case, the sampled distribution (bars) reflect a Normal distribution, with parameters listed at the bottom of the plot.
- Close both Histogram Views by selecting the X in the upper right corner of each view.
6.3 SCATTER PLOTS
Scatter plots allow you to examine the relationship between any two analysis variables. You can generate a scatter plot of results using the Scatter Plot dialog.
- Select Plot Scatter
 on the toolbar or the Statistics menu.
on the toolbar or the Statistics menu. - In the Scatter Plot dialog, select the variables you would like to plot on the X and Y axes. For example, let’s plot the Toppling Joint Dip (X Axis Dataset) versus the Factor of Safety (Y Axis Dataset).
- Select the Highlight Data check box.
- Click OK to generate the plot.
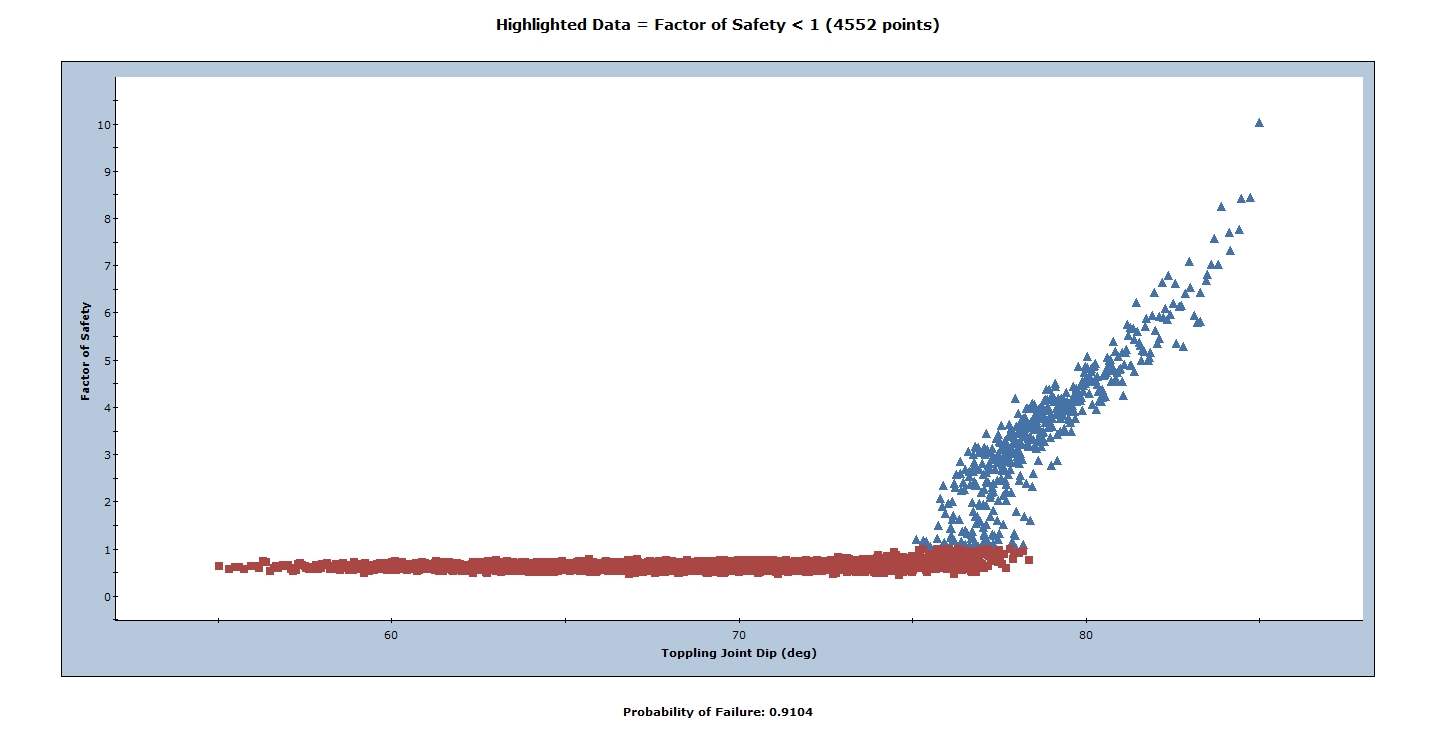
From the plot, we can see that the slope is generally more stable for steeply dipping toppling joints. This is reasonable considering blocks topple when their weights fall outside of the block base. Thus, for a block of the same aspect ratio, its weight will gradually fall outside the base as it’s gradually tilted. It is also the reason why a threshold is clearly observed in the graph: past a certain toppling joint dip, blocks start toppling.
To fit a line of regression to the scatter plot:
- Right-click on the graph and select Regression Line.
The alpha and beta values of the regression line are shown at the bottom of the plot.
Note the following:
- The alpha value (-6.59) represents the y-intercept of the linear regression line on the scatter plot.
- The beta value (0.107) represents the slope of the linear regression line.
- The Correlation Coefficient indicates the degree of correlation between the two variables plotted. This value varies between -1 and 1, where a number close to 0 indicates a poor correlation, and a number close to 1 or -1 indicates a good correlation. A negative Correlation Coefficient indicates the slope of the regression line is negative.
You are encouraged to experiment further with the Probabilistic analysis features of RocTopple using other options on the chart right-click menu (e.g., Plot in Excel and Change Plot Data).
This concludes the tutorial. You are now ready for the next tutorial, Tutorial 03 - Slope Design in RocTopple with Eurocode 7.