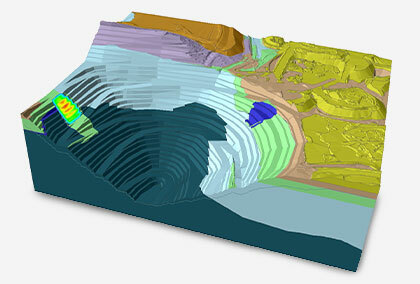
Does 3D Slope Stability Analysis Always Produce Higher Factors of Safety than 2D?
By Reginald Hammah and Frema Awuku-Asabere
A lot has been written about 3D slope stability analysis generating factors of safety that can be higher than 2D results by up to 20%. But is this true? We do not believe so.
We believe that 3D slope stability analyses do not inherently produce higher safety results than 2D. They only solve the problem specified in a model.
Let us examine this issue using a finite element formulation of the Shear Strength Reduction (SSR) method. In numerical analysis, plane strain 2D conditions exist in geotechnical problems (for example, slope stability models) constrained in the direction perpendicular to the analysis plane. 2D analysis either corresponds to a “very long” slope in the out-of-plane direction or one that is constrained in that direction; it has zero displacement (and thus zero strains) along the out-of-plane axis.
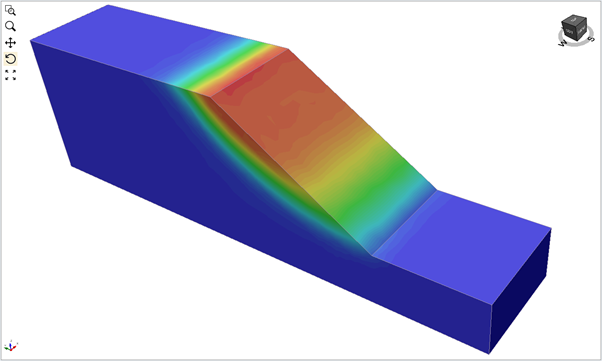
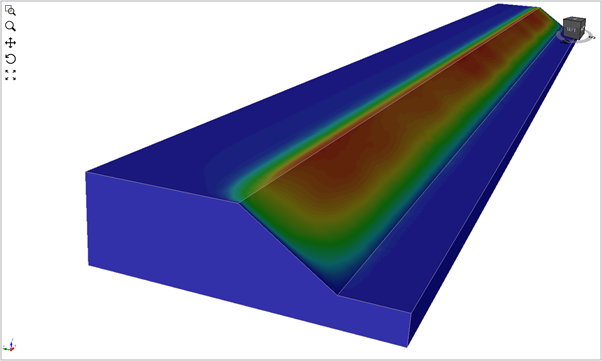
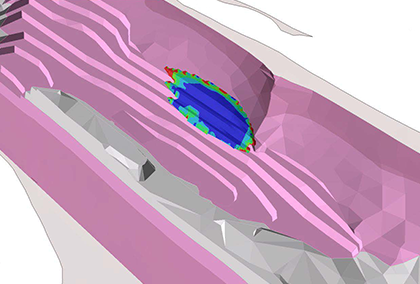
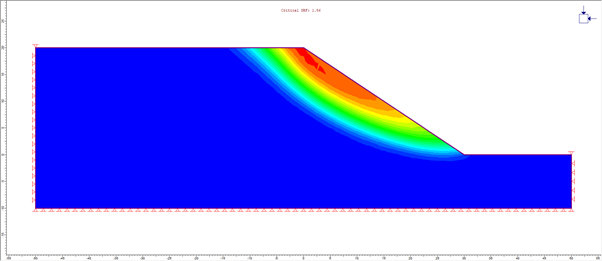
We can model 2D problems in 3D using two different approaches. We can use thin (along slope strike) models with appropriate roller-type displacement boundary conditions in the first approach. These do not inhibit in-plane displacements, while they at the same time eliminate end effects. Alternatively, we can build an extended model (along the slope strike) that ensures that end effects have a near-zero impact on results. Figures 1 and 2 below show the safety results for the two approaches, and the results are nearly identical to the 2D answers (Figure 3).
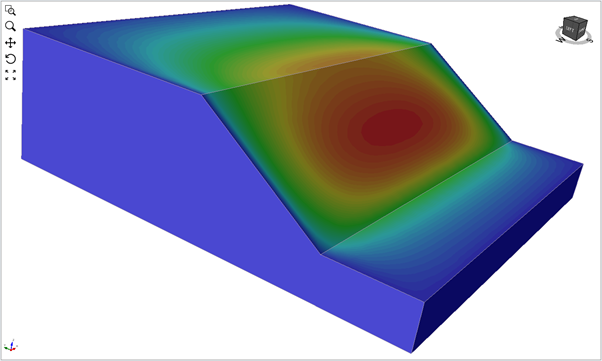
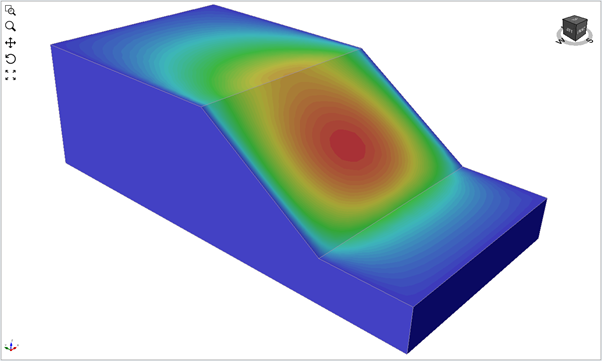
If we were to make the slope shorter while using fully constrained sides, end effects begin to affect safety factors. The less extended we make the slope, the more significant the role of the end effects, and the higher the factor of safety value. We can see this in Figures 4 and 5.
This simple thought experiment shows that 3D is not inherently over-optimistic compared to 2D. If we build 3D models that reflect actual 2D conditions, we get very similar answers with 2D. If 3D models do not adequately capture 2D situations, then end effects could change results.
We look forward to more trials, but we are confident they will continue to confirm our findings.
The experiments have also had one effect on our thinking. Suppose slope conditions are such that displacements in the out-of-plane direction are extensional instead of being zero (or compressional as occurs with fixed end conditions). Would that not mean that 3D factor of safety will be lower than 2D? We will check that out in the next issue. Until then, stay safe.