Structural Solutions by RS2 - Problem of Stacked Beams

Introduction

This article is intended to show the power of RS2 in solving a complicated structural problem. The problem chosen is the well-known stacked beams problem. It is known that if you stack identical simply supported beams made of elastic material under any distributed loading the load effect will be distributed equally to each of the stacked beams.

For a simply supported beam subject to uniformly distributed load or concentrated load, the bending moment at mid-span will respectively be,

M = wL²/8

M = PL/4

where,

w = uniformly distributed load, units of F/L

P = concentrated load at mid-span, units of F

L = length of beam, units of L

What happens if you have three smooth beams stacked together? For example, if you have 3 stacked beams such as the ones shown in Fig.1(a) or Fig.1(b) the resulting bending moment at the middle of the beams will be one-third of the above values. This is based on the theory of beams. But if you analyze the problem as a continuum the results will be different as the concentrated load gets distributed along the depth of the beams.

The original problem

A beam was subject once to uniformly distributed load w (case A) and another to a concentrated load P (case B). The load P is half the resultant of the distributed load w such that they both produce the same bending moment at mid-span, i.e., P = wL/2. A laborer got afraid of the beam failing to hold the loads. He added two stacked beams on the original beam, all symmetrical. The question is in which case will the bottom beam get less bending moment?

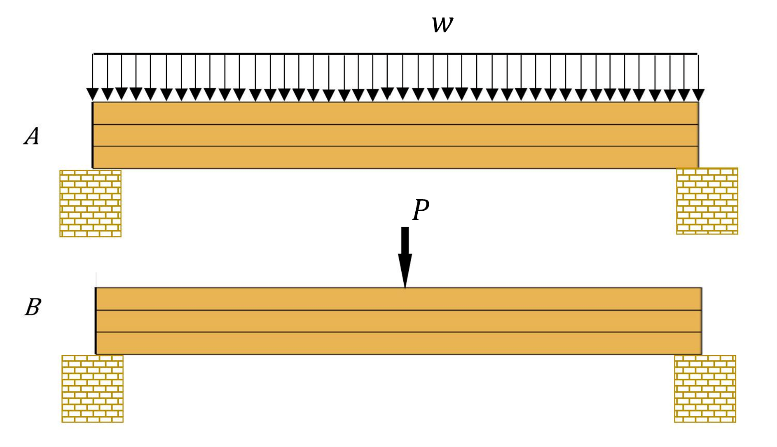
Answer and reason:

Eventually, following the beam theory, the bending moment at each beam will be equal to one-third of the original moment. Here comes the surprise: As the beam has a depth continuum theory will distribute the concentrated load and turn it from a point load at the top beam to a distributed load at the bottom beam.

The answer is “Case B”.

In case A, the load will be transmitted to the lower beams as is so keep the reduction in the bending moment uniform. In case B, the concentrated load gets distributed to a length that increases in the following beams and hence will decrease the moments. The distribution takes place due to the thickness of the beam (a beam with no thickness cannot distribute by thickness) and due to the subsurface reaction of the following beam (like a subgrade reaction) which arises from “springs” that can be assumed corresponding to the varying bending stiffness of the beam deflecting below the above beam.

Note that, the answer is based on no friction or connection between the beams. Each beam acts individually but of course, not independently.

Proof by an RS2 Finite Element Model

Using the 2D FEM program, RS2, a software product of Rocscience Inc., the three beams may be modeled easily. Nevertheless, some considerations shall be taken while assigning properties to materials and interfaces.

In the following, a numerical example is introduced. To simulate a model, first, dimensions and materials shall be chosen reasonably. The beam's dimensions are taken as 22 ft in length 1 ft in width, and 0.5 ft in thickness. The material is chosen with a smooth surface (no friction material). A modulus of elasticity of 2E8 psf and a yield strength of 2E6 psf with a Poisson’s ratio of 0.25 are decided. These are given as elastic plastic material with a friction angle of zero and a cohesion of 1E6 psf in a Mohr-Coulomb model. Limit for tensile strength may be specified as well as 2E6 psf. No body forces are applied, i.e., the beams are weightless (the answer, being case B, will not get affected by self-weight addition as it is the same in both cases).

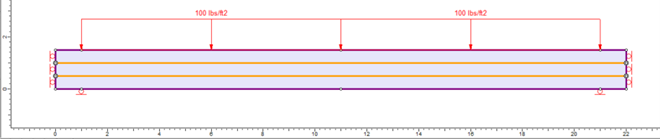
The beams are stacked on two supports as shown in Fig. 2 below with a length of 20 ft between supports. The reason for not taking the supports at the ends is to show symmetric stress concentration near the supports.

To separate the beams from each other, joints shall be used in RS2. This provides an interface layer in FEA. The joints shall have no shear stiffness, a very low value of 1E-12 psf/ft is used, and a normal stiffness close to the modulus of the material is used, 2E8 psf/ft. While the joints must fail in holding tension, the tensile strength of the joint is eliminated, and the shear strength is not effective as the shear stiffness is very low already. The joints are “open-ended” and have two rows of nodes.

And because of numerical nature of the analysis and no lateral loads are applied, it is better to replace the hinge by rollers at the same point and on the side centers of the beams as shown in Fig.3.

Loads

In Case A, a uniformly distributed load, UDL, w = 100 lb/ft is chosen, to give a bending moment at midspan of a single beam of 5000 lb. ft, and in turn, causes a tensile stress of 120000 psf as Mc/I.

Hence, the corresponding concentrated load that gives similar moment and stress is 1000 lb.

When the UDL is applied to the stacked three beams the bending moment is divided by the three beams equally and the resulting tensile stress at the bottom will be 40000 psf.

If the results show a tensile stress at the bottom less than 40000 psf then Case B is the answer, and the proof is done.

The loads are shown in Fig.3.

Meshing

The mesh setup in RS2 is chosen as graded mesh of 6-noded triangular elements with 400 external nodes. Part of the mesh from the left side is shown in Fig.4.

Results

The target is the tensile strength at the extreme bottom fiber of the original beam. The execution of the model resulted a value of 38952 psf, compared to the results obtained for tensile stress at the bottom beam of 39978~40000 psf in the UDL case. The results of the concentrated load model are shown in Fig.5. The top positive figure shown is the compressive stress at the top fiber.

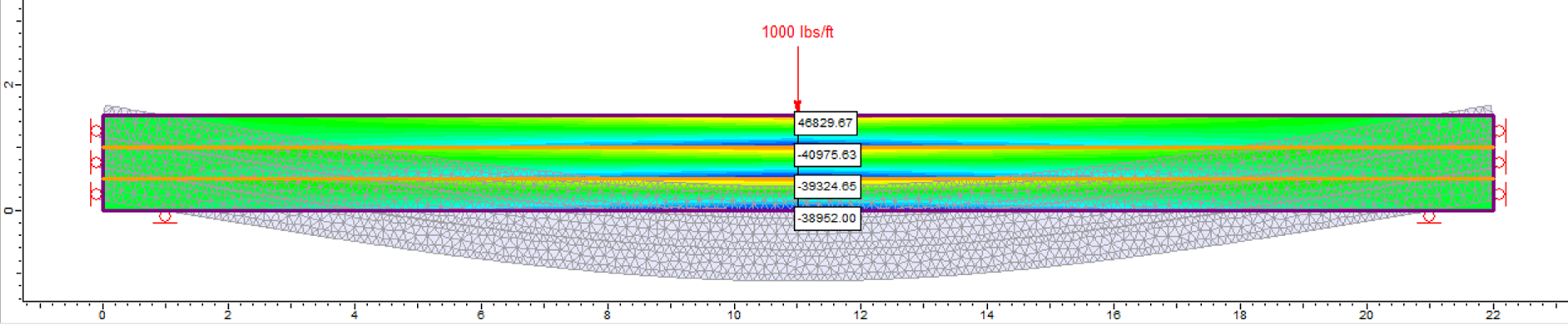
Another check for the model is that the results should show a vertical stress everywhere (except the concentrated zones near the vertical supports and the concentrated loads) of zero (or near zero because of the numerical nature of FEA). Meanwhile, the vertical displacement (deflection) shall be equal vertically for the three beams for each distance as shown in Fig.6.

The results are affected by the thickness of the beams and the stiffness of the beams. As the beam's thickness decreases the stress distribution is less effective and as the stiffness of the beams decreases the stress at the bottom increases.

Conclusion

Continuum mechanics distributes the stresses more accurately than beam theories. Within the usual traditional practice, the error is insignificant but as beam thickness increases the beam theories deviate more from the correct stress distribution.

RS2 may adequately be used for modeling structural continuum problems.

References:

Boresi, A.P. and Sidebottom, O.M. (1985): “Advanced Mechanics of Materials”. John Wiley and Sons, New York, USA.

Popov, E.P. and Balan T.A. (1998): “Engineering Mechanics of Solids”. 2^nd ed., Prentice Hall, New Jersey, USA.