RLEM & SAO: Effective Probabilistic Analysis in Less Computational Time
Probabilistic analysis can be a powerful tool for slope stability to account for the variability in subsurface conditions (Spatial variability) and this can be especially effective when working with challenging soil properties.
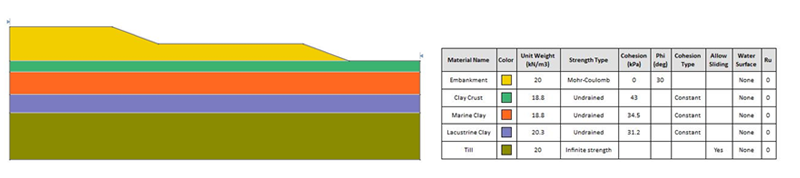
This research paper (Javankhoshdel et al., 2021) presented at the Rocscience International Conference 2021, presents a Limit Equilibrium Method (LEM) based hybrid optimization technique which combines a local search algorithm with a global search method to accurately identify the critical slip surface with computational efficiency which is necessary for the probabilistic analysis considering spatial variability of soil properties. To demonstrate this, a case study of the James Bay Dyke in northern Ontario was selected. Figure 1 shows the created model as well as the soil properties.
Surface Altering Optimization is a local search algorithm which modifies the geometry of a slope to minimize the factor of safety. It does this by systematically modifying the coordinates of the 2D spline curve in multiple iterations until convergence criteria is met. SAO was used in finding the lowest factor of safety (FS) in both the deterministic and Random Limit Equilibrium (RLEM) analyses conducted in this study. RLEM is a probabilistic analysis that uses the Limit Equilibrium Method (LEM) to compute minimum FS by considering the spatial variability of soil properties.
James Bay Dyke Case Study
A deterministic analysis identified a critical slip surface with a factor of safety (FS) of 1.17 (Figure 2a). To verify the results, a Shear Strength Reduction (SSR) analysis was also conducted in RS2 and a Shear Strength Reduction Factor (SRF) of 1.22 was generated along with the maximum shear strain contours, shown in Figure 2b.

An important consideration for all engineers performing numerical analysis is computational time. The combination of LEM and SAO is a faster process than FEM, and this difference is compounded when you consider probabilistic analysis, where you need to run thousands of realizations.
RLEM Analysis with SAO
The RLEM analyses were run with soil properties expressed as isotopic random fields with spatial variability in the horizontal and vertical directions. The shear strength of the materials were assigned random variable parameters using normal (Gaussian) distributions. Three different analyses were run using different spatial correlation lengths (5, 15, 30m) where 10,000 Latin Hypercube simulations were run for each length.
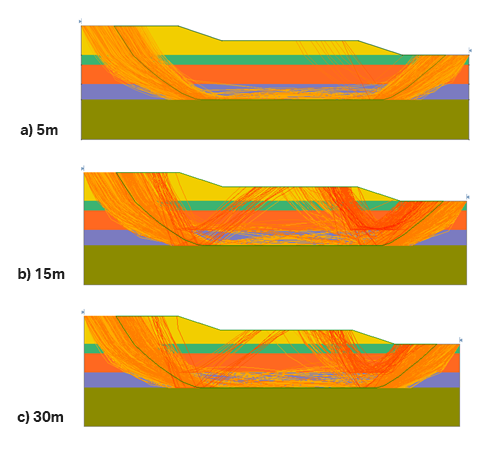
The results from these simulations indicate that as the spatial correlation length increases, the probability of failure increases as well. The mean FS values of the RLEM analyses were 1.08968, 1.052, and 1.04 for 5m, 15m, and 30m, respectively. Based on these results and looking at the failure surface bands (Figure 3), the longer the correlation length, the more failure surfaces appear with shorter lengths in the middle regions of the model. This is likely caused by large regions of soil to sample weak parameters. On the other hand, with the 5m correlation length (Figure 3a), the strong neighboring soil regions likely offsets the reductions in material strength making failure in the middle of the model less likely.
Further verification of these results are shown in Figure 4. The soil shear strength is plotted in colour and FS values of a short failure surface and a longer slip surface are shown. Both failure surfaces pass through the weakest material (blue regions) in Figure 4a and b.

Figure 5a and 5b are SSR analyses for the same fields presented in Figure 4a and 4b, respectively. It can be seen in Figure 5a and 5b, that the same failure mechanisms were captured as in Figure 4a and 4b. This verifies the ability of the RLEM approach and SAO to find the weakest failure paths and is in good agreement with the failure paths captured by SSR analysis for the same field.

This case study showcases how RLEM analysis with spatially variable soil layers combined with SAO, can correctly identify the weakest failure paths of a model. Slide2 has once again proven how effective it can be by not only identifying critical slip surfaces but also by saving valuable time computing probabilistic analyses.
Start a free trial of Slide2 today or visit our learning resources for more information about how you can get the most out of your software tools.