by T. R. Stacey, Professor Emeritus, University of the Witwatersrand

ABSTRACT

In the Introduction to this paper, many names are mentioned of those with African origins or associations, who have made significant contributions in the field of rock engineering. Then important considerations in rock engineering are considered, focusing on the African contributions. These considerations include rock engineering design; rock mass characterisation; rock material strength and factors affecting its value - specimen geometry, moisture content, temperature and time; rock mass classification; rock mass strength and deformation parameters; boundary conditions; and numerical modelling. Finally, a section dealing with geotechnical value and a suggested Quantified Value-Created Process for decision making in mining is presented.

INTRODUCTION – AFRICA’S CONTRIBUTIONS TO ROCK ENGINEERING

As an introduction, I would like to summarise the rock mechanics and rock engineering “Rich History” with roots in Africa. I believe I am qualified to review this “rich history” since I began my career in rock mechanics in South Africa in 1968. After that, I shall focus on what, in my opinion, are principal considerations in rock engineering. References that I quote will deliberately focus on authors from the African continent.

Experts of African origins or associations who have made significant rock engineering contributions to the world include Hoek, Bieniawski, Cook, Salamon, Wagner, Ortlepp, Laubscher, van der Merwe and many others. The authors of one of the early rock mechanics publications included four of these names (Cook et al, 1966).

Owing to the extensive mining operations and challenging ground conditions in South Africa, there was an early need for rock mechanics and engineering research. This work started in the 1940s, although rockbursting occurred much earlier and some gold mines were already deep. Rock mechanics research began in the 1940s at the Council for Scientific and Industrial Research (CSIR), while the Chamber of Mines Research Organisation (COMRO) was established in the 1950s. A major collapse in a coal mine, which caused many deaths, further spurred the research requirements. These two facilities became a rock mechanics research powerhouse that grew to more than 600 research staff. Two of the first publications dealing with rockbursts in South African mines were by Hill (1954) and Roux and Denkhaus (1954). Denkhaus became the Director of the National Mechanical Engineering Research Institute, which housed the Rock Mechanics Division (in the Mechanical Engineering Institute because of the focus on stresses and strains). Hoek (originally from Zimbabwe) was an early Head of this Division, followed in 1966 by Bieniawski. Members of the Division who made significant contributions included Hoek (rock fracture and failure), Bieniawski (rock fracture, rock mass classification), Leeman and van Heerden (in situ stress measurements), and Vogler (rock property testing). Others were John (rapid loading properties), Stacey (rock slope stability, 2D and 3D finite element stress analyses) and Pells (various contributions, including point load testing). Bieniawski facilitated research activity for many younger rock engineers, including Philip Pells, one of the best engineers I have known and a friend of more than 50 years. He later gained his doctorate from the University of Cape Town. Another friend of more than 50 years, Uli Vogler, is a specialist in rock testing, whose results can be trusted implicitly. He was active in rock testing research as recently as 2014 (Vogler, 2014); and Willie van Heerden who specialised in in situ stress measurement and was also very capable in other fields. Bieniawski, Vogler and van Heerden contributed significantly to the Suggested Methods of the International Society for Rock Mechanics, each providing experienced input into at least five Suggested Methods. At COMRO, there were also many notable rock engineering researchers, including Salamon, Wagner, Cook, Gay, Napier, Ryder, Jager, Joughin, Spottiswoode, Durrheim, van der Merwe, Gurtunca and others. In Mining Engineering at the University of the Witwatersrand, rock engineering academics have included Budavari, Ozbay, Stacey, van der Merwe, Yilmaz and Watson. In the field of rockbursts and seismicity in mines, Durrheim is contributing significantly. Starfield was a Professor of Applied Mathematics at the University and was also briefly on the staff of the Mining Engineering Department. In addition to the very early publications mentioned above, authors of early, notable rock mechanics publications were Salamon et al. (1964), Ortlepp and Nicoll (1964) and Plewman et al. (1969).

Following the major coal mine collapse, Salamon and Munro (1967) conducted fundamental research on coal pillar design. Further research on coal pillars has been carried out more recently by Madden (1991), van der Merwe (2003), and van der Merwe and Mathey (2013).

The Muller Award is the most prestigious award of the International Society for Rock Mechanics and Rock Engineering (ISRM). The first two of these awards went to Hoek and Cook, originally from Africa. The Rocha Medal of the ISRM has been awarded annually since 1982 for the best PhD (internationally) in rock mechanics. Up to 2021, students who carried out their research in South Africa have been awarded this medal more than any other country. These include Brummer, Daehnke, Hildyard, Malan, Linzer (nee Anderson), du Plessis, and a runner-up, Watson. Also, Van der Merwe served a term as President of the ISRM.

At least forty professors in the geotechnical field (current and past) developed or honed their skills in Africa. These include Suorineni and Chitombo, both of whom have made significant international contributions. Ortlepp, although not an academic, also deserves notable mention for his extensive research into rockbursts and seismicity in mines (Ortlepp, 1997). He made very valuable contributions to rock mechanics and engineering for over 50 years. He developed and tested yielding rockbolts in the 1960s to counter rockburst damage (Ortlepp, 1969). Unfortunately, this development was never commercialised, and it was only in the 1990s that yielding conebolts were developed and tested at COMRO (Jager, 1992). Ortlepp also developed yielding rock support elements commercialised as Durabar (Ortlepp and Erasmus, 2005; Bornman et al, 2001), Duracable (Ortlepp et al., 1991) and Duramesh. I believe that Ortlepp was responsible for the employment of Dr. Aleks Mendecki by Anglo American. Mendecki developed a company in the field of seismicity monitoring in mines, which grew to provide international hardware, software and monitoring interpretation services. It is now the Institute for Mine Seismicity (IMS), based in Australia, and still provides services to mining companies worldwide.

IMPORTANT CONSIDERATIONS IN ROCK ENGINEERING

In this section, important considerations in rock mechanics and rock engineering will be dealt with, including relevant examples and contributions from the African continent.

Rock Engineering Design

Good rock engineering design should follow a design process. Figure 1 (Stacey, 2009) depicts a design process based on design principles and methodology developed by Bieniawski (1992), modified into a wheel of design.

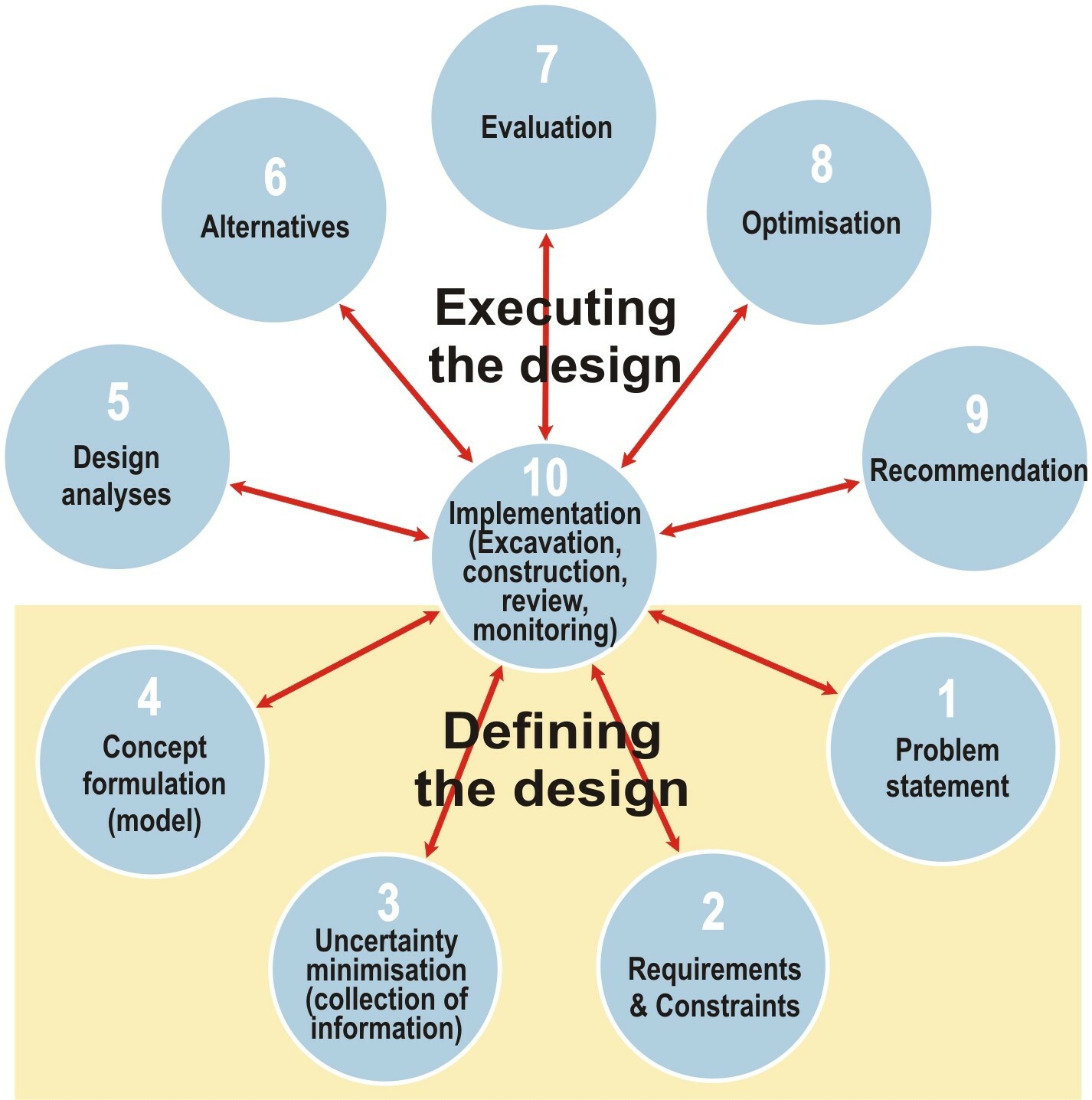
As shown in Figure 1, the process is divided into two phases: defining the design, and executing the design. The first two steps define the objectives of the design, and step 3 involves rock mass characterisation. Step 4, the formulation of the conceptual model, is probably the most important step in the process. Developing a conceptual model involves identifying expected behaviour in order to establish appropriate design criteria.

Review and monitoring are essential in ensuring that actual behaviour corresponds with the expected behaviour. The spokes of the wheel indicate that the process should return to earlier steps if actual performance does not match expected behaviour. Diligent adherence to such a process will ensure a good design. Personal experience from several civil rock engineering contractual dispute cases has demonstrated that problems are likely to be experienced if any step in the design process is overlooked.

Rock Mass Characterisation

Any design in rock engineering requires good knowledge of the properties of the rock mass, hence the importance of good rock mass characterisation, corresponding with Step 3 of the above design process. This characterisation is often challenging owing to the inherent variability in rock masses. It is difficult enough in civil engineering, where excavations are well defined. In mining, however, new excavation surfaces are constantly exposed, openings advance, and it is often neither practical nor economical to carry out detailed investigations. It is also often the case that design information is lacking due to a reluctance to incur the costs of obtaining such data. We, therefore, often do not know what is to come in the “new” excavations; and, as stated by Wong (2005), “Reliability cannot be predicted without statistical data; when no data are available the odds are unknown.” It is often necessary to consider uncertainty using probability and risk approaches. Generally, the greater the uncertainty, the greater the risk. Minimisation of uncertainty involves geotechnical investigations to provide input data for engineering design. This fact emphasises the importance of step 3 of the design process in generating value for the mining project. Risk has been proposed as a rock engineering design criterion (Stacey et al, 2007). Steffen (Steffen, 1997; Terbrugge et al, 2006) was a strong proponent of the probability and risk approach. He gained experience in the mining field at an open pit copper mine in Zambia and, subsequently, in consulting to many mines worldwide. Steffen, with Robertson and Kirsten, established the consulting company now known as SRK Consultants in 1974, specialising in geotechnics. SRK is now international, with offices in many countries, and serves many mining operations in Africa. Many postgraduate students gained their masters degrees in South Africa whilst working as employees or interns in SRK’s Johannesburg office. Terbrugge, a long time colleague, has consulted on many open pits in Africa and elsewhere.

One method for taking into account “unknown” rock mass structural characteristics is to use discrete fracture networks (DFN). Since the “standard” distributions of jointing parameters (orientation, length and spacing) are known, a good estimate of the means and ranges of these parameters, provided by an appropriately experienced geotechnologist, will generally allow good quality DFNs to be produced. Therefore, even with no measured data, it is often possible to prepare satisfactory DFNs that are particularly useful at scoping and pre-feasibility levels. It must be emphasized that a DFN is simply one representation of a rock mass. Numerous DFNs must be generated to evaluate behaviour, associated risks, and failure probabilities.

An early, simple DFN method was developed in South Africa (Haines, 1983; 1984) for application in a tunnel contractual dispute case. Rockfalls occurred during the excavation of a railway tunnel, and it was necessary to evaluate the contractor’s associated claims. Over its full length, the tunnel traversed five rock types with different geotechnical characteristics. The predicted total volume of rockfalls using the simple DFN approach was 86m³, which compared closely with the measured volume of 82m³ of the actual rockfalls. This simple DFN method was subsequently applied with success in numerous other cases (Stacey et al., 2015). Kuppusamy (2021) recently used a DFN approach for the design of open pit benches.

A further example of this DFN approach was in the prediction of rockfalls in tabular stopes in deep-level gold mines. Since no published data on jointing parameters were available, Gumede (2006) carried out conventional mapping of joints in two stopes of a gold mine to establish the jointing statistics (Gumede and Stacey, 2007). Using these statistics, DFNs were created to evaluate the potential for rockfalls. The predicted height of rockfalls was compared with empirical data presented by Daehnke et al. (2001). The empirically indicated heights of rockfalls in the two stopes were 1.8m and 2.2m, and the DFNs predicted identical heights, proving the value of the DFN approach.

The probability of occurrence of rockfalls, defined by joint planes, in tabular stopes in South African platinum mines was researched by Rwodzi (2011), Nezomba (2012) and Joughin et al. (2012a; 2012b). Use was made of a probabilistic software product called Jblock developed by Esterhuizen (2003), who grew up in Zimbabwe, and gained mining degrees and experience in consulting and academia in South Africa. He is now at NIOSH in the USA. The research using Jblock demonstrated the significant benefit to both safety and economics of reducing the occurrence of rockfalls by increasing the support installed (Rwodzi et al., 2011).

As part of the characterisation of a rock mass, it is necessary to measure the strength of the rock material. Two civil engineering examples illustrate the importance of this. In the first example, a tunnel contractual dispute case in Africa initially related to the jointing in the rock mass and its effect on overbreak. However, the relevance of the rock strength subsequently became important. No rock strength data were provided in the contract documents, and it was found that no tests had been carried out. Subsequent uniaxial compressive strength (UCS) tests carried out on behalf of the contractor proved that the rock material was much stronger than could have been interpreted from the information in the contract documents. This higher strength, which negatively affected blasthole drilling rates and tool wear, was an added basis for the contractual claim.

The second example also involved a contractual dispute in Africa. This case involved a quarrying operation to provide large blocks of rock for breakwater purposes. Rock UCS test data were included in the contract document, and it was stated that the tests were carried out according to international standards. Independent testing carried out on behalf of the contractor during the contract proved that the rock strength was approximately twice that stated in the contract document. The high strength adversely affected drilling rates, blasting, and equipment wear. It was found that the quality of rock specimen preparation was at fault, with the flatness and parallelity of UCS specimen end surfaces not being to standard. The result was a finding in favour of the contractor.

Rock strength testing is usually carried out under normal laboratory conditions. When making use of these data in rock engineering design, in which ambient conditions may be very different from those in the laboratory, some of the important influencing factors are:

Specimen geometry: strength results from laboratory tests are influenced by the specimen geometry. Both uniaxial and triaxial tests show that the strength is “constant” only when the length to diameter ratio of the specimens is 2.5 or greater (Vogler and Stacey, 2016; John, 1972).

Moisture: Colback and Wiid (1965) measured a UCS reduction from a dry specimen to a saturated specimen of up to 50%. This effect has also been shown by many other international authors.

Temperature: Oniyide (2015) studied the effect of temperature on the strength and deformation properties of South African Bushveld Complex rocks, relevant to deep-level platinum mining. The effects of temperature on strength and deformation properties of two brittle rock types are shown in Figure 2.

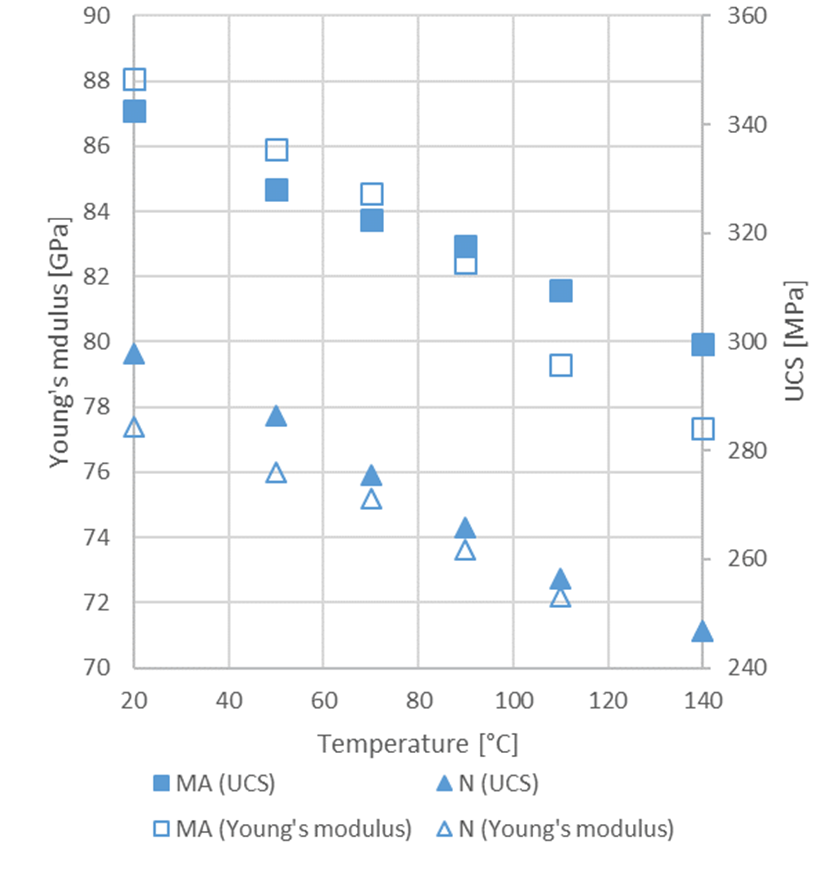
These results indicate that for the temperatures likely to be experienced in deep-level mining and tunnelling, the reduction in compressive strength due to temperature will typically be about 15%, and the reduction in modulus of elasticity will typically be about 10%. Oniyide’s test results indicated that Poisson’s ratio is unaffected, and cohesion and angle of friction are only marginally reduced (1–2%), for a 100^oC increase in temperature.

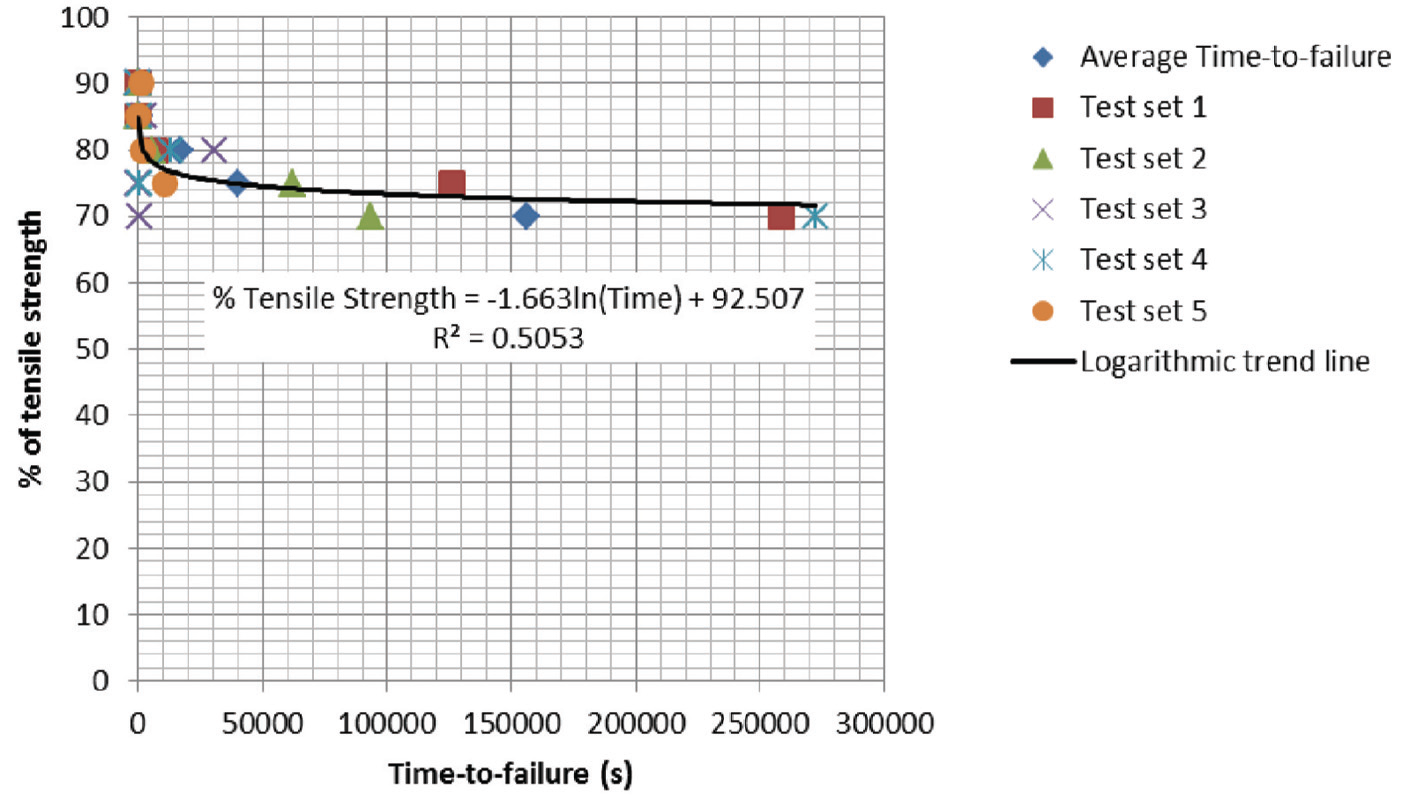
Time: in all projects, rock loading will be for very much longer periods than that in laboratory tests. Longer-term tests on Bushveld Complex igneous rocks, representative of deep-level platinum mining in South Africa, were carried out by Nyungu (2013). The results indicate long-term UCS values of 44% to 72% of the standard laboratory test value; and the long-term Brazilian indirect tensile strength values are in the range of 60% to 70% of the short-term strengths, as shown in Figure 3.

Rock Mass Classification

Rock mass classification has become a vital tool in rock engineering due to its ability to quantify the quality of rock masses and to use the rock mass “number” to evaluate rock mass strength and deformation properties. Interestingly, the developers of three of the methods in common use in the world gained their original rock engineering skills in the African environment: Bieniawski (1973) developed his Rock Mass Rating System whilst at the CSIR; the Mining (or Modified) Rock Mass Rating System was developed in the caving mining environment in Zimbabwe (Laubscher and Taylor, 1976; Laubscher, 1990); and Hoek (1999) developed the Geological Strength Index more recently in Canada. This history is somewhat surprising since classification systems have not found wide use in the harsh mining environment in South Africa’s deep level, high stress, and brittle rock conditions.

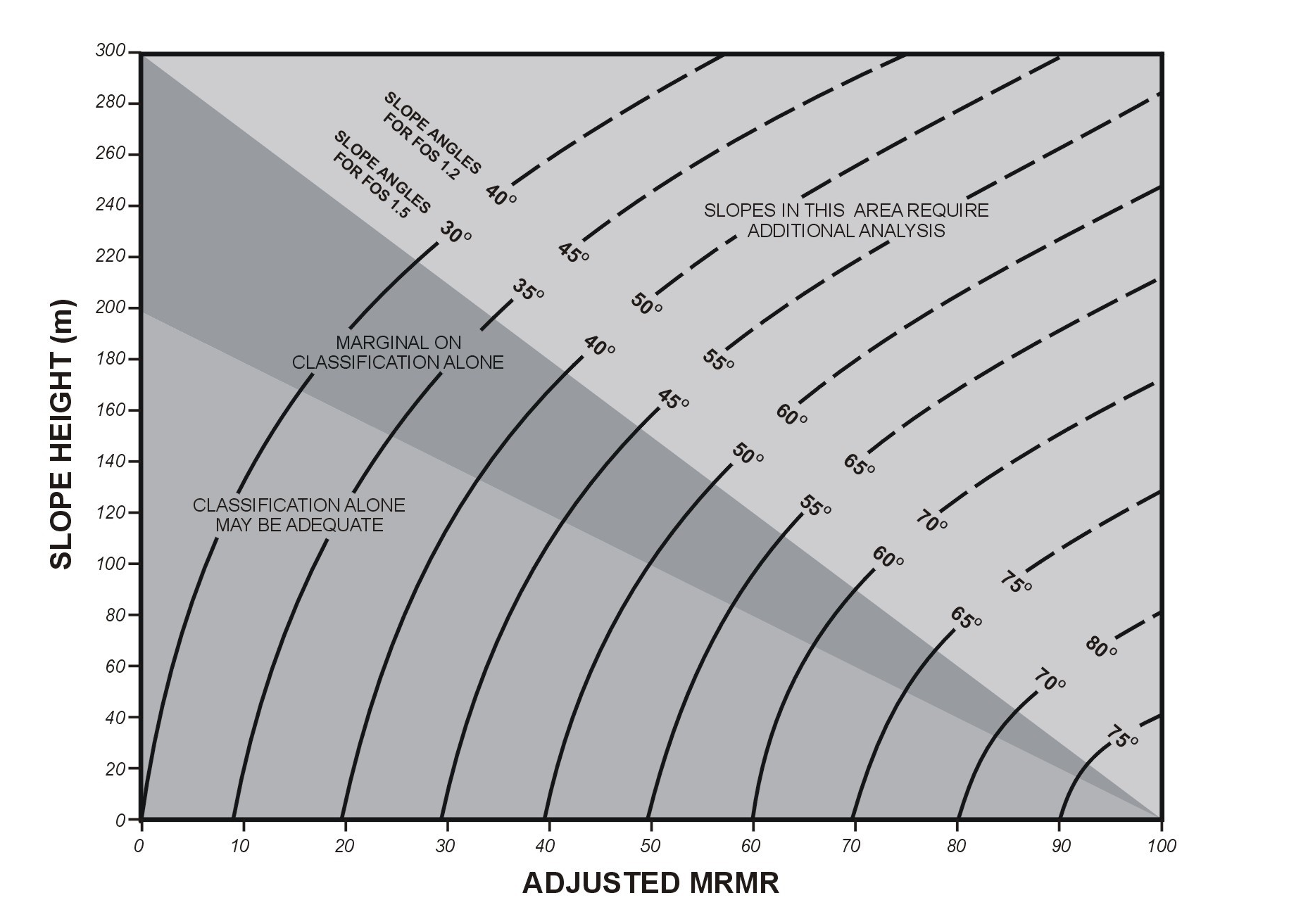
Two South African adaptations of rock mass classification systems, which have found international usage, are the Raisebore Reliability Index Q_R (McCracken and Stacey, 1989) and the Empirical Slope Design Chart developed by Haines and Terbrugge (1991). The raisebore stability evaluation method is an adaptation of Barton’s Q System (Barton et al, 1974). It is used widely internationally, particularly in Australia, where it has been further developed by Peck and coworkers (for example, Peck and Lee, 2008). The Empirical Slope Design Chart is based on Laubscher’s classification system. This chart, shown in Figure 4, was very useful for rapid prefeasibility evaluations of potential open pit slopes in Chile. It was found that predicted slope angles differed very little from those designed later using robust analysis methods. The chart was also incorporated into the geotechnical block model developed by Bye (2003), which allowed rapid determination of suitable slope angles for each “block” of an open pit mine.

Rock Mass Parameters

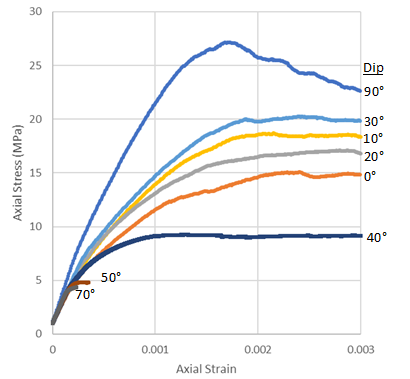
The availability of a quantified rock mass quality has facilitated its use in estimating rock mass strength and deformation parameters. The Hoek-Brown failure criterion (for example, Hoek et al., 2002), and the empirical correlations between the rating value and rock mass modulus (Hoek and Diederichs, 2006), are examples. Such estimations have proven to be very useful in rock engineering design, where a factor of safety or probability of failure is usually adopted. However, the strength and deformability of jointed rock masses will vary depending on the loading directions since there are six moduli and three Poisson coefficients in the three-dimensional elastic stress-strain relationship. This variability is illustrated clearly in the graph below, which shows stress-strain curves for an anisotropic rock mass loaded in different directions, determined from synthetic rock mass analyses (Bester, 2019). This directionally dependent behaviour must be considered when predicting in rock engineering (Stacey and Wesseloo, 2022).

It is also important for prediction that the correct mechanism of failure is taken into account. In this regard, extension fracturing is common in brittle rocks, and an extension strain failure criterion has been proposed for initiation and failure of such rocks (Stacey, 1981; Wesseloo and Stacey, 2016).

Boundary Conditions

The design of any excavation in rock requires the boundary conditions to be adequately defined. In situ stresses are fundamental boundary conditions. The creation of extensive openings in mining locally changes the in situ values and creates a new set of field stresses in the vicinity of excavations. Pioneering work on in situ stress measurement methods was carried in South Africa by Leeman (1964a; 1964b; 1968) and van Heerden (1976), involving the development of the doorstopper and triaxial strain cells. Stress measurements are often difficult to carry out in the early stages of a mining project, and thus the in situ stress field is often assumed, not measured, and these assumptions may or may not be appropriate. If the assumed values are incorrect, the design or analysis may be wrong, or, at best, inadequate.

Many in situ stress measurements have been made for mining and major civil engineering projects in Southern Africa. A research project to review and evaluate available stress measurement data for the mining industry was conducted by Stacey and Wesseloo (1998a; 1998b). This project was subsequently extended to Southern Africa (Stacey and Wesseloo, 1999) and further updated (Wesseloo and Stacey, 2006). The research produced a database of in situ stress measurement results, and interpretations of in situ stress directions from seismic records over the area covered by the physical measurements. This database represents a means of realistically estimating in situ stresses in the region, for early evaluation of projects, when no physical data are available. Figure 6 illustrates the locations at which some in situ stress information is available in the database.

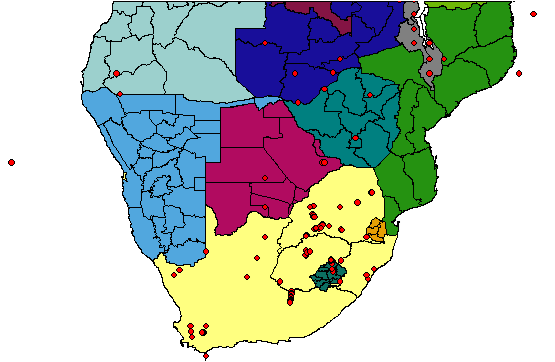
Figure 6. Locations of data points for the in situ stress database

Numerical Modelling

The development and use of stress analyses in mining in South Africa began in the 1960s. Early elastic analyses of mine workings were carried out using an electrical analogue (Salamon, 1963; 1964; Ortlepp and Nicoll, 1964; Ryder and Officer, 1964). The availability of computers in the late 1960’s led to the increasing use of numerical methods for rock engineering analyses in mining and civil engineering projects. Deist (Plewman et al., 1969) wrote the original mining simulation analysis (MINSIM) program used for stress analysis and simulation (planning) of tabular mining. Stacey (1969; 1970) applied a finite element package for mining stress analyses. This was subsequently modified to allow non-linear, continuum analysis of jointed rock masses. It was simplified by Van Heerden and Kovacs (1979) and later rewritten by Diering (1981) to run on a small minicomputer (Stacey et al., 1981). It was used in a rock engineering consulting environment for about 20 years until commercial products with good graphics facilities became available. Programs were also written to allow analyses of mining problems in three dimensions (Stacey, 1972; 1973; Deist et al, 1973). However, the life of these programs was limited owing to the development of boundary element programs which were much less demanding on computing times. Diering (1982; 1987) developed two- and three-dimensional boundary element programs. The latter was regularly used to analyse mining problems (for example, Diering and Stacey, 1987; Stacey et al., 1991). This program was also used in Canada for a while. Diering’s career changed from rock engineering to mine planning, and, while in South Africa, he developed a mine planning system for block caving mines in conjunction with Laubscher, which he named PCBC. Diering moved to Canada with the mine planning software company GEMCOM. PCBC was developed further, and is now offered by Dassault Systemes GEOVIA. It is used internationally by most caving operations.

The following philosophy, summarised from Starfield and Cundall (1988), is extremely important when planning any numerical modelling activity. The publication by Diering and Stacey (1987) is also relevant.

• Be sure about why you are building a model and what questions you expect to answer.

• Use a model to provide early results and understanding at the earliest possible stage. A good conceptual model can provide value.

• Identify expected mechanisms of behaviour, deformations and likely modes of failure.

• Experiment with the model to gain understanding and eliminate inconsistent behaviour.

• Use the simplest model that will allow the essential mechanisms to occur, which can serve as a test-bed for your problem.

• Choose a simple experiment and compare the results with your expected behaviour. If there is an agreement, proceed to more complex experiments; if not, identify the weaknesses in your thinking or the model's shortcomings, and remedy them before continuing.

• If your model has weaknesses (e.g. you only have a 2D model for 3D problem), run analyses that will bracket the real case.

• Once you have sufficient experience with your simple model, you can run more complex models as required.

This philosophy corresponds well with the rock engineering design process (Bieniawski, 1992; Stacey, 2009). Visualizing and anticipating solutions before running a model is a necessary discipline, and this corresponds with step 4 of the rock engineering design process in Figure 1: Conceptual formulation (model). There is often a misconception that analysis is design, and many sophisticated analyses, with little underlying validity in terms of input data and failure criteria, are often carried out. It may be observed from the above steps that "analysis," which involves analytical (including numerical), empirical and observational methods, occupies only one step of the overall design process. Analysis is a tool to obtain answers to the problem posed. If the input information is inadequate or the conceptual model is incorrectly formulated, the answers obtained from analyses may be scientifically correct, but they will be wrong regarding a valid design because the sophisticated analyses have provided results for the wrong problem.

Design and Prediction

There is a significant difference between design and prediction in rock engineering (Stacey and Wesseloo, 2022). Numerical design approaches and failure criteria are well established in rock engineering for the conditions commonly encountered in civil and mining situations. Empirical methods are also applicable in known conditions, and unknowns can be addressed by increasing the Factor of Safety. This is not the case, however, in new conditions – for example, the deep level, more competent, confined rock conditions now being experienced in mines and tunnels. Here, prediction of behaviour is necessary so that likely fracture and failure criteria can be identified, to allow for rational design. Prediction is much more difficult than design under “new” conditions. The correct mechanisms of rock and rock mass failure must be identified to allow rational analyses to be carried out. Such mechanisms are fundamental for the prediction of behaviour. Failure initiation may be by one mechanism, propagation by another, and ultimate failure by other mechanisms.

GEOTECHNICAL VALUE

Rock engineers can create considerable value for mining operations and save on contractual claims in civil engineering projects. The value is not only in financial terms but also in the areas of health and safety, and in social aspects such as extended employment periods. The latter benefits employees, their dependents, the community. Value is also created by careful management of the environment. When considering decisions, conventional risk evaluation processes tend to focus on negative aspects such as costs and potential losses. In mining, the major loss in value resulting from a negative event is commonly the loss of production. A decision-making process, based on a quantitative evaluation of the created value, which focuses on the upside or positive aspects, has been proposed (Stacey and Hadjigeorgiou, 2022). This Quantified Value-created Process (QVP) for decision-making in mining, is shown in Figure 7. It is a further development of the design process shown in Figure 1, and the strategic planning method developed by Ilbury and Sunter (2005).

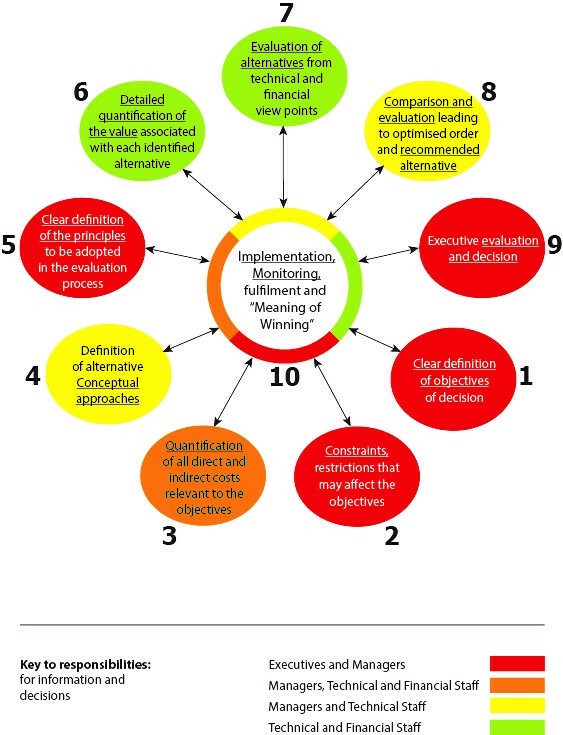
Figure 7. Quantified Value-created Process for decision making in mining (Stacey and Hadjigeorgiou, 2022)

The QVP requires significant input from executives, particularly in the early stages, to ensure that ethical and responsible decisions are made and that good consideration is given to short, medium and long-term strategies. Quantification of the inputs to the process, as required by the executives, will be supplied by mine management personnel and mine technical specialists, who have access to the appropriate costing information and records of past performance on the mine. These records include accidents, damage, collapses, dilution, loss of production, etc., and associated costs, and will allow the benefits of additional investment to be quantified. Examples include the value created by installing better, but more costly, rock support (Moganedi, 2019) and the value of improved geotechnical monitoring to provide timely indications of any instabilities, which might have safety and economic implications. The ultimate decision on the chosen option is again the responsibility of the executives, based on the quantified value-created data. This QVP is a logical decision-making system that will result in decisions that will greatly benefit the planning and operation of mines.

CONCLUSIONS

The section above dealing with value was deliberately placed just before the conclusions so that the value created for the world’s rock engineering community by those who originated or passed through Africa could be summarised. Names of some who have made major contributions from Africa, have been mentioned already, and some will be mentioned again here, mainly from personal knowledge. Apologies are made for the lack of mention of many others who have also made significant contributions.

All will be aware of the contributions made by Hoek: early research into rock fracture and as Head of the Rock Mechanics Division at the CSIR in Pretoria; then, his contribution while at Imperial College, London - he made analysis of rock slopes easy; PhD students while he was there included Nick Barton and Peter Cundall, both now very well recognized names. Subsequently, he developed the Hoek-Brown failure criterion and the GSI System. Next, I mention Bieniawski, who took over from Hoek as Head of the CSIR Rock Mechanics Division. After his rock fracture research, Bieniawski’s major contribution was the RMR rock mass classification system, and later, in the USA, his rock mechanics design principles and methodology. He also developed his rock excavability system.

At COMRO, Cook made an outstanding contribution on rockbursts and seismicity in mines. He co-authored the excellent rock mechanics textbook (Jaeger and Cook, 1969). Salamon fundamentally contributed to the field of coal pillar design. Cook, Salamon and Wagner continued to make rock engineering contributions in the USA and Austria.

For many years at the University of the Witwatersrand, Budavari was a magnificent teacher of rock mechanics. Ortlepp made significant contributions to rockburst research and rock support under rockburst conditions. Laubscher made major contributions in mining with caving methods.

REFERENCES

Barton, N., Lien, R. and Lunde, J. (1974) Engineering classification of rock masses for the design of tunnel support, Rock Mech., Vol 6, No 4, pp 189-236.

Bester, M. (2019) A risk based methodology to improve the definition of geotechnical design sectors in slope design, PhD Thesis, University of the Witwatersrand.

Bieniawski, Z.T. (1992) Invited Paper: Principles of engineering design for rock mechanics, Rock Mechanics, Proc. 33^rd U S Symp. on Rock Mech., Ed. Tillerson & Wawersik, Balkema, pp 1031-1040.

Bornman, J.J., Ortlepp, W.D. and Stacey, T.R. (2001) The impact of Durabar^TM yieldable tendons on the safety and cost implications of support spacing, Proc. 4^th Int. Conf. Roofbolting in Mining, Wissenschaftsverlag Mainz in Aachen, pp 395-408.

Butcher, R.J. (2000) A modelling method for predicting block cave cavability, initial fragmentation and production tonnage at a scoping study level, MSc Research Report, University of the Witwatersrand.

Bye, A. (2003) The development and application of a 3D geotechnical model for mining optimisation, Sandsloot Open Pit Platinum Mine, South Africa, PhD Thesis, University of Natal, 203p.

Cook, N.G.W., Hoek, E., Pretorius, J.P.G., Ortlepp, W.D. and Salamon, M.D.G. (1966) Rock mechanics applied to the study of rockbursts, Jl S. Afr. Inst. Min. Metall., 66, pp 435-528.

Deist, F.H., Salamon, M.D.G. and Georgiades, E.A. (1973) A new digital method for three-dimensional stress analyses in elastic media, Rock Mech., Vol. 5, pp 189-202.

Diering, J.A.C. (1987) Advanced elastic analysis of complex mine excavations using three-dimensional boundary element techniques, D. Eng Thesis, University of Pretoria.

Diering, J.A.C. (1982) Further developments of the boundary element method with applications in mining, MSc Thesis, University of the Witwatersrand.

Diering, J.A.C. (1981) QUAD – a finite element programme for no-tension Mohr-Coulomb failure and jointed rock analysis on a small mini computer, Internal Report, Steffen, Roberston and Kirsten Inc, SE208/2

Diering, J.A.C. and Stacey, T.R. (1987) Three-dimensional stress analysis: a practical tool for mining problems, APCOM 87: Proc. 20th Int. Symp. on Application of Computers and Mathematics in the Mineral Industries, v 1: Mining, S. Afr. Inst. Min. Metall., pp 33-42.

Esterhuizen, G.S. (2003) JBLOCK User Manual.

Gumede, H. (2006). Development of data sets on joint characteristics and consideration of associated instability for a typical South African gold mine. MSc Dissertation, University of the Witwatersrand.

Gumede, H. and Stacey, T.R. (2007) Measurement of typical joint characteristics in South African gold mines and the use of these characteristics in the prediction of rock falls, Jl S. Afr. Inst. Min. Metall., vol. 107 , no. 5 , pp 335-344.

Haines, A. (1983) The quantitative assessment of potential tunnel instability by extrapolation of rock mass discontinuity mapping. In Proceedings of the Symposium on Rock Mechanics in the Design of Tunnels, 1-5, S. Afr. National Group of Int. Soc. Rock Mech.

Haines, A. (1984) The application of generated rock mass discontinuity patterns. In Proceedings of the Eighth Regional Confernce for Africa on Soil Mechanics and Foundation Engineering, Harare, 13-21. A A Balkema, Rotterdam.

Haines, A. and Terbrugge, P.J. (1991) Preliminary estimation of rock slope stability using rock mass classification systems, Proc. 7^th Int. Cong. Int. Soc. Rock Mech., Aachen, Balkema, Vol. 2, pp 887-892.

Hill, F.G. (1954) An investigation into the problem of rockbursts. An operational research project. Part 1. The approach to the problem and analysis of the rock bursts that have occurred on the ERPM during the years of 1948-53, Jl Chemical, Metallurgical and Mining Society of South Africa, October, pp 63-72.

Hoek, E. (1999) Putting numbers to geology - an engineer's viewpoint, Quart. Jl Engng Geol., Vol. 32, pp 1-19.

Hoek, E., Carranza Torres, E. and Corkum, B. (2002) Hoek-Brown Failure Criterion – 2002 Edition. NARMS, Toronto.

Hoek, E. and Diederichs, M.S. (2006) Empirical estimation of rock mass modulus, Int. J. Rock Mech. Min. Sci., 43(2), 203-215.

Ilbury, C. and Sunter, C. (2005) The games foxes play – planning for extraordinary times, Human and Rousseau Tafelberg, 180p.

Jaeger, J.C. and Cook, N.G.W. (1969) Fundamentals of Rock Mechanics, Methuen.

Jager, A.J. (1992) Two new support units for the control of rockburst damage, Proc. International Symposium on Rock Support, Sudbury, Laurentian University.

John, M. (1972) The influence of the length to diameter ratio on rock properties in uniaxial compression: a contribution to standardisation in rock mechanics testing, Geomechanics Internal Report ME1083/5, CSIR Pretoria.

Joughin, W., Jager, A., Nezomba, E. and Rwodzi, L. (2012a) A risk evaluation model for support design in Bushveld Complex underground mines: Part I – Description of the model. Jl S. Afr. Inst. Min. Metall. 112: 2, 83-94.

Joughin, W., Jager, A., Nezomba, E. and Rwodzi, L. (2012b) A risk evaluation model for support design in Bushveld Complex underground mines: Part II – Model validation and case studies. Jl S. Afr. Inst. Min. Metall. 112: 2, 95-104.

Kuppusamy, V. (2021) Application of discrete fracture networks (DFN) to the design of open pit benches in rock slopes, MSc Dissertation, University of the Witwatersrand.

Laubscher, D.H. (1990) A Geomechanics Classification System for the Rating of Rock Mass in Mine Design. Journal of the Southern African Institute for Mining and Metallurgy, 90(10), pp. 257-273.

Laubscher, D.H. & Taylor, H.W., (1976) The Importance of Geomechanics Classification of Jointed Rock Masses in Mining Operations, Proceedings of the Symposium on exploration for Rock Engineering. Johannesburg, A.A. Balkema, pp. 119-128.

Leeman, E.R. (1964a) The measurement of stress in rock, Parts I and II, Jl S. Afr. Inst. Min. Metall., 65 (2), 45-113.

Leeman, E.R. (1964b) The measurement of stress in rock, Part III, Jl S. Afr. Inst. Min. Metall., 65 (4), 254-284.

Leeman, E.R. (1968) The determination of the complete state of stress in rock using a single borehole – laboratory and underground measurements, Int. J. Rock Mech. Min. Sci., 5, 31-56.

Madden, B.J. (1991) A re-assessment of coal pillar design, Jl S. Afr. Inst. Min. Metall., 91 (1), 27-37.

McCracken, A. and Stacey, T.R. (1989) Geotechnical risk assessment for large-diameter raise-bored shafts, Trans IMM, Section A, v 98, pp A145-A150.

Moganedi, K.A. and Stacey, T.R. (2019) Value creation as an approach to the management and control of rockburst damage in tunnels, Tunnelling and Underground Space Technology, 83, pp545-551.

Nezomba, E. (2012) Use of joint trace data to evaluate stability of mining excavations, and validation against underground observations, MSc Dissertation, University of the Witwatersrand.

Nyungu, D. (2013) Effect of time on the tensile strength of several Bushveld Complex rock types, MSc Dissertation, University of the Witwatersrand.

Nyungu, D. and Stacey, T.R. (2014) Time-dependent tensile strengths of Bushveld Complex rocks and implications for rock failure around mining excavations, Proc. SARES 2014, S. Afr. Inst. Min. Metall., pp 69-84.

Ortlepp, W.D. (1997) Rock Fracture and Rockbursts – an illustrative study, Monograph Series M9, S. Afr. Inst. Min. Metall., 255p.

Ortlepp, W.D. (1969) An empirical determination of the effectiveness of rockbolt support under impulse loading, Proc, Int. Symp. on Large Permanent Underground Openings, Oslo, September 1969, Brekke and Jorstad (eds), Universitatsforlaget, pp 197-205.

Ortlepp, W.D., Bornman, J.J. and Erasmus, P.N. (2001) The Durabar – a yieldable support tendon – design rationale and laboratory results, Proc RASIM %, Rockbursts and Seismicity in Mines, S. Afr. Inst. Min. Metall., 263-266.

Ortlepp, W.D. and Erasmus, P.N. (2005) Dynamic testing of a yielding cable anchor, Proc. 3^rd Southern African Rock Engineering Symposium, S. Afr. Inst. Min. Metall., 13p.

Ortlepp, W.D. and Nicoll, A. (1964) The elastic analysis of observed strata movement by means of an electrical analogue, Jl S. Af. Inst. Min. Metall., 64(6), pp 214-231.

Peck, W.A. and Lee, M.F. (2008) Stability of raise bored shafts in Australian mines, 13^th Australian Tunnelling Conference, Melbourne, 4-7 May 2008.

Plewman, R.P., Deist, F.H. and Ortlepp, W.D. (1969) The development and application of a digital computer method for the solution of strata control problems, Jl S. Afr. Inst. Min. Metall., 69(), pp 33-44.

Roux, A.J.A. and Denkhaus, H.G. (1954) An investigation into the problem of rockbursts. An operational research project. Part II. An analysis of the problem of rock bursts in deep level mining, Jl Chemical, Metallurgical and Mining Society of South Africa, November, pp 103-124.

Rwodzi, L. (2011) Rockfall risk: quantification of the consequences of rockfalls, MSc Dissertation, University of the Witwatersrand.

Rwodzi, L., Joughin, W. and Stacey, T.R. (2011) Rockfall risk — how well do we understand the consequences of the decisions we make?, Proc. Strategic 2011, Proc. 4^th Int. Seminar on Strategic vs Tactical Approaches in Mining, Perth, Australian Centre for Geomechanics, pp 179-194.

Ryder, J.A. and Officer, NC (1964) An elastic analysis of strata movement observed in the vicinity of inclined excavations, Jl S. Afr. Inst. Min. Metall., 64(6).

Salamon, M.D.G. (1963) Elastic analysis of displacements and stresses induced by the mining of seam or reef deposits, Part I, Jl S. Afr. Inst. Min. Metall., 64(4).

Salamon, M.D.G. (1964) Elastic analysis of displacements and stresses induced by the mining of seam or reef deposits, Part II, Jl S. Afr. Inst. Min. Metall., 64(6).

Salamon M.D.G. and Munro, A.H. (1967) A study of the strength of coal pillars, Jl S. Afr. Inst. Min. Metall., 68, pp 55-67.

Stacey, T.R. (1969) Application of the finite element method in the field of rock mechanics with particular reference to slope stability, S. Afr. Mech. Eng., v 19, Dec 1969, pp 131-134.

Stacey, T.R. (1970) The stresses surrounding open pit mine slopes, in Planning Open Pit Mines, ed P W J van Rensburg, A A Balkema, 1970, pp 199-207.

Stacey, T.R. (1972) Three-dimensional finite element stress analysis applied to two problems in rock mechanics, Jl S. Afr. Inst. Min. Metall., v 72, no 10, May 1972, pp 251-256.

Stacey, T.R. (1973) A three-dimensional consideration of the stresses surrounding open pit mine slopes, Int. J. Rock Mech. Min. Sci., v 10, 1973, pp 523-533.

Stacey, T.R. (1981) A simple extension strain criterion for fracture of brittle rock, Int. J. Rock Mech. Min. Sci., v 18, 1981, pp 469-474.

Stacey, T.R. (2009) Design – a Strategic Issue, Jl S. Afr. Inst. Min. Metall., Vol 109, No 3, pp 157-162.

Stacey, T.R., Armstrong, R. and Terbrugge, P.J. (2015) Experience with the development and use of a simple DFN over a period of 30 years, Mining Technology, Vol 124, No 3, pp 178-187.

Stacey, T.R., Diering, J.A.C. and Rigby, N.R. (1991) Stability predictions based on back analysis of collapsed crown pillar, Epoch Mine, Zimbabwe, Proc. Symp. African Mining ‘91, Harare, Zimbabwe, pp 55-60.

Stacey, T.R. and Hadjigeorgiou, J. (2022) Quantified Value-created Process (QVP) – a value-based process for mine design and operating decisions, Jl S. Afr. Inst Min. Metall., 122 (2), pp 73-82.

Stacey, T.R., Terbrugge, P.J. and Wesseloo, J. (2007) Risk as a rock engineering design criterion, in Y. Potvin, J. Hadjigeorgiou and T.R. Stacey (eds), Challenges in deep and high stress mining, Australian Centre for Geomechanics, Perth, pp. 17-23.

Stacey, T.R., Van Heerden, W.L. and Diering, J.A.C. (1981) Analysis of excavations in jointed rock, Proc. Conf. on Finite Element Methods in S. Afr., Nat. Inst. for Aeronautics and Systems Technology of the CSIR and S. Afr. Inst. of Aero. Engrs., March 1981, 16pp.

Stacey, T.R. and Wesseloo, J. (1998a) Evaluation and upgrading of records of stress measurement data in the mining industry, Report Safety in Mines Research Advisory Committee (SIMRAC), GAP511b, June 1998.

Stacey, T.R. and Wesseloo, J. (1998b) In situ stresses in mining areas in South Africa, Jl S. Afr. Inst. Min. Metall., 98(7), pp 365-368.

Stacey, T.R. and Wesseloo, J. (1999) The in situ stress regime in Southern Africa, Proc. 9^th Int. Cong. Int. Soc. Rock Mech., Paris, Volume 2, Balkema, pp 1189-1192.

Stacey, T.R. and Wesseloo, J. (2022) Design and prediction in rock engineering: the importance of mechanisms of failure, with focus on high stress, brittle rock conditions, Rock Mech. Rock Eng., 55, 1517–1535.

Steffen, O.K.H. (1997), ‘Planning of open pit mines on a risk basis’, Jl S. Afr. Inst. Min. Metall., (97) 2, Mar/Apr, 47-56.

Terbrugge, P.J., Wesseloo, J., Venter, J. & Steffen, O.K.H. (2006), A risk consequence approach to open pit slope design, Jl S. Afr. Inst. Min. Metall., (106) 7, 503-511

Van der Merwe, J.N. (2003) New pillar strength formula for South African coal, Jl S. Afr. Inst. Min. Metall., 103, 281-292.

Van der Merwe, J.N. and Mathey, M. (2013) Probability of failure of South African coal pillars, Jl S. Afr. Inst. Min. Metall., 113, pp 849-857.

Van Heerden, W.L. (1976) Practical application of the CSIR triaxial strain cell for rock mass measurements, Proc. ISRM Symp. Investigation of Stress in Rock, Advances in Stress Measurement, Sydney, pp1-6, Institute of Engineers, Australia.

Van Heerden, W.L. and Kovacs, I.K.A. (1979) Two-dimensional stress analysis of jointed rock – computer programme ROCKJNT, Rep. Coun. Scien. Ind. Res. S. Afr., ME1601/4, 56p.

Vogler U.W.O.L. (2014) Evaluation of stiff testing of rock, MSc Dissertation, University of the Witwatersrand.

Vogler, U.W.O.L. and Stacey, T.R. (2016) The influence of test specimen geometry on the laboratory-determined class II characteristics of rocks, Jl S. Afr. Inst. Min. Metall., Vol 116, No 11, November, pp 987-1000.

Wesseloo, J. and Stacey, T.R. (2006) Updated in situ stress database for Southern Africa, Proc. Int. Symp. on In-situ Rock Stress, Trondheim, Norway, June 2006, Taylor & Francis/Balkema, pp 467-471.

Wesseloo, J. and Stacey, T.R. (2016) Reconsideration of the extension strain criterion, Rock Mech. Rock Eng., Vol 49, No 12, December, pp4667-4679.