Beta Statistical Distribution
The Beta distribution is a very versatile function which can be used to model several different shapes of probability density curves, as shown below.
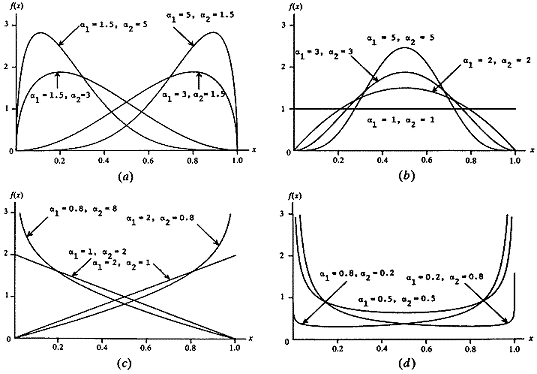
The form of the Beta distribution is determined by the shape parameter a1 and a2. Both a1 and a2 are always > 0. The relationship between the Beta distribution shape parameters and the UnWedge input data is as follows:
![]()
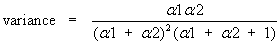
The standard deviation is the positive square root of the variance.
Note that the above equations apply to a beta random variable on [0,1]. To re-scale and relocate to obtain a beta random variable on [a,b] of the same shape, use the transformation a + (b–a)X