Anisotropy - Two Planes
1.0 Introduction
This model demonstrates a simple homogeneous slope, with TWO planes of anisotropy at different orientations. The Generalized Anisotropic Strength function is used. For more details regarding definition of anisotropic plane with strength parameters, please refer to Generalized Anisotropic Overview.
2.0 Material with Two Anisotropic Planes
This model demonstrates a simple homogeneous slope, with TWO planes of anisotropy at different orientations. The Generalized Anisotropic Strength function is used.
- Select File > Recent > Tutorials in the menu and open the file Anisotropy – Two Planes
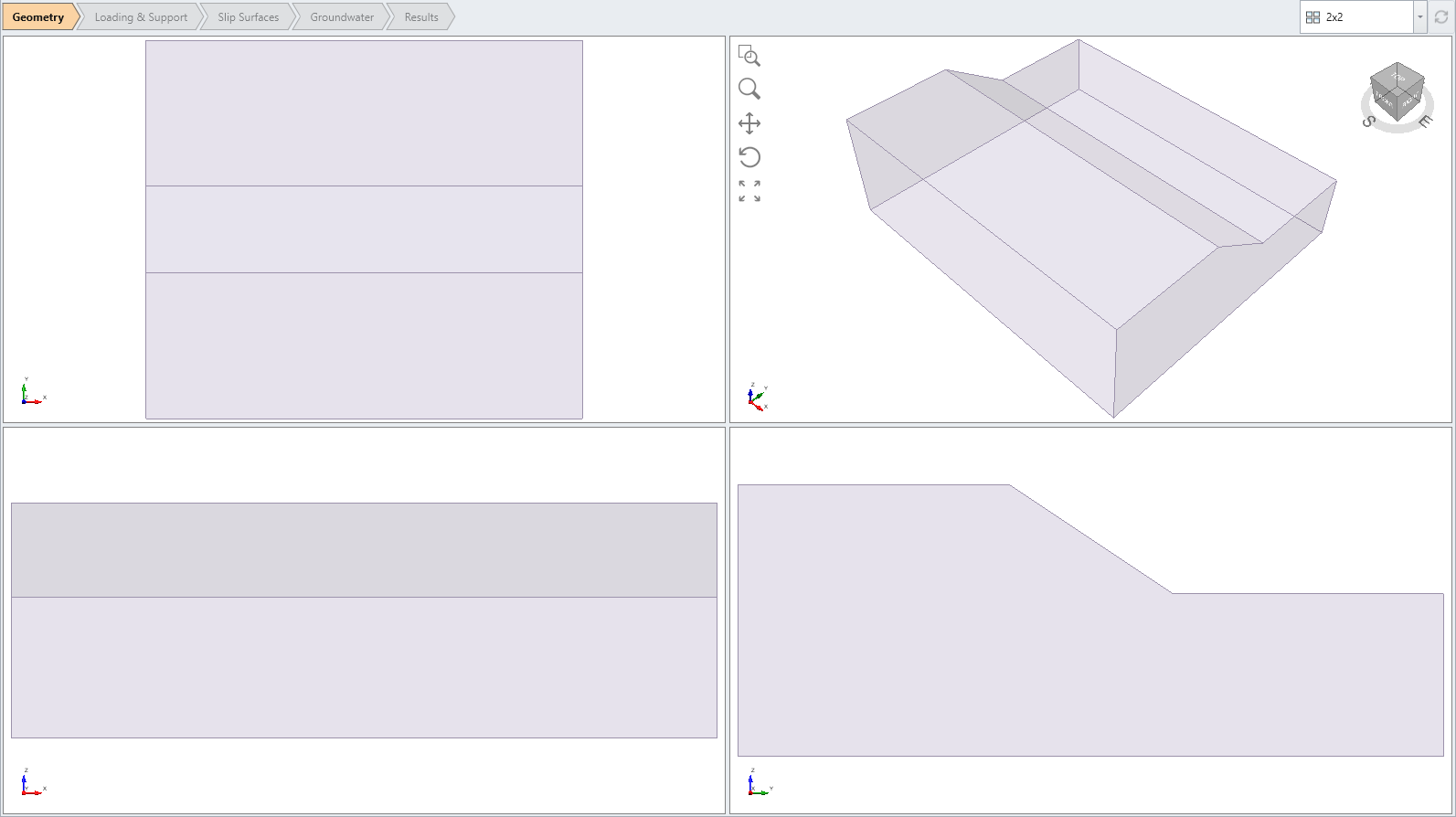
The model is a single material 2D slope extruded to 3D. - Select Materials > Define Materials

- For the anisotropic material, select the Edit
 button beside the Generalized Function combo box.
button beside the Generalized Function combo box.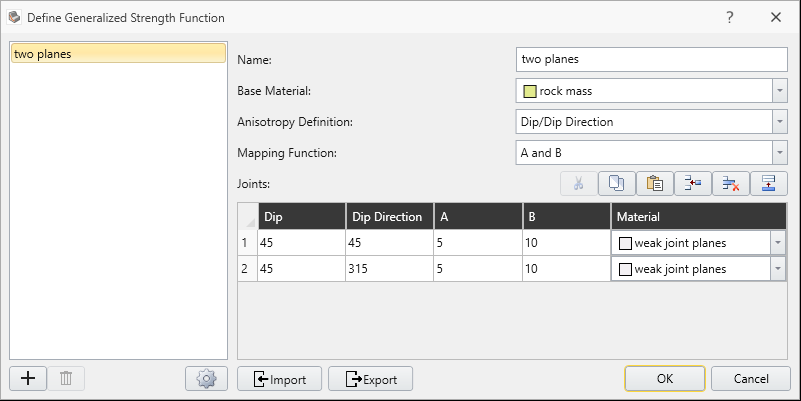
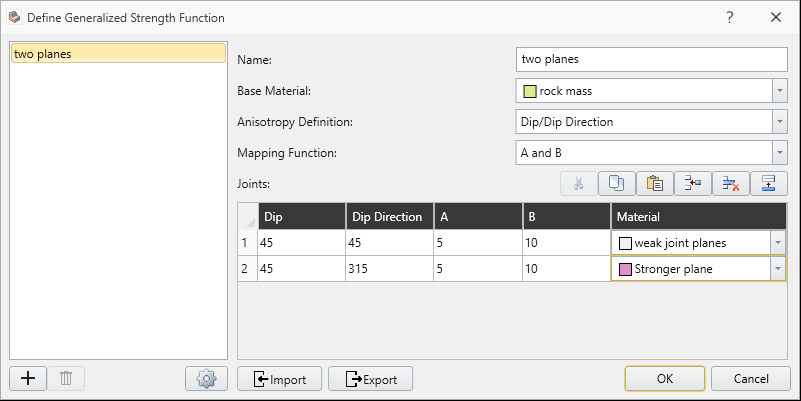
- Make sure the following parameters are entered.
- Anisotropy Definition = Dip/DipDirection
- Mapping Function = A and B
- Two anisotropic planes are defined
- Dip = 45 Dip Direction = 45
- Dip = 45 Dip Direction = 315
- A parameter = 5 (both planes)
- B parameter = 10 (both planes)
- Base Material = “rock mass”
- Anisotropic plane Material = “weak joint planes”
- Run Compute

- Select the Results workflow tab

- Turn on the contours by selecting Show contour
 from toolbar.
from toolbar. - Change the contour data to Shear Strength.

- Change the contour data to Base Friction Angle.
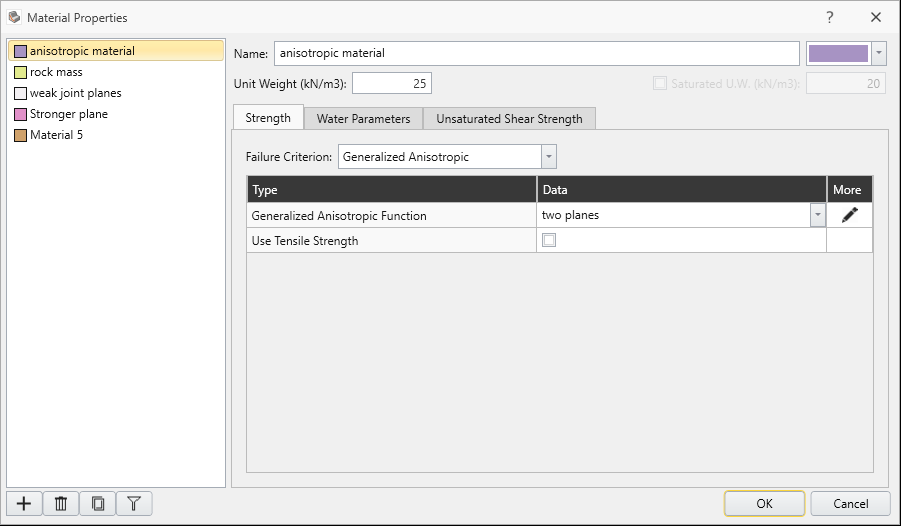
Notice the four materials defined: anisotropic material, rock mass, weak joint planes, stronger plane.
For the Bishop method, the global minimum surface should appear as follows. Safety factor = 1.2. Base Normal Stress contours are displayed in the following figure.

You can clearly see the shear strength of the two planes (blue contours) which intersect to form a wedge-like failure surface.
This clearly highlights the low friction angle (15 degrees) of the two weak planes (blue colour) in contrast to the higher strength of the failure surface at other orientations.

3.0 Two Planes of Different Strength
As an additional exercise, we will assign the stronger material to the second plane.
- Click on anisotropic material properties, and under the Generalized function dialog, select edit and assign the Stronger material to the second plane.
- Save with a new file name and select Compute
 to re-run the analysis.
to re-run the analysis. - Change the contour data to Shear Strength.

- Change the contour data to Base Friction Angle.
Notice that the critical slip surface is now slightly asymmetric, and the Bishop safety factor is slightly higher than the previous result, since we increased the strength of one of the anisotropic planes.
You can clearly see the different friction angle of the two anisotropic planes (blue = 15 degrees, light blue = 20 degrees).

This concludes the Slope with Two Anisotropic Planes tutorial.