Snowden Mod. Anisotropic Linear
The Snowden Modified Anisotropic Linear strength model is based on the Anisotropic Linear strength model, with the following additional features (Snowden, 2011): 1- allows you to define non-linear stress dependent strength envelopes for the rock mass and bedding material in a tabular format
2- allows non-symmetric anisotropy.
The Snowden Modified Anisotropic Linear model allows you to define a non-symmetric anisotropy function as shown in Figure below, using four parameters A1, A2, B1 and B2. Compare this with the symmetric function for the Anisotropic Linear model which only uses two variables A and B.
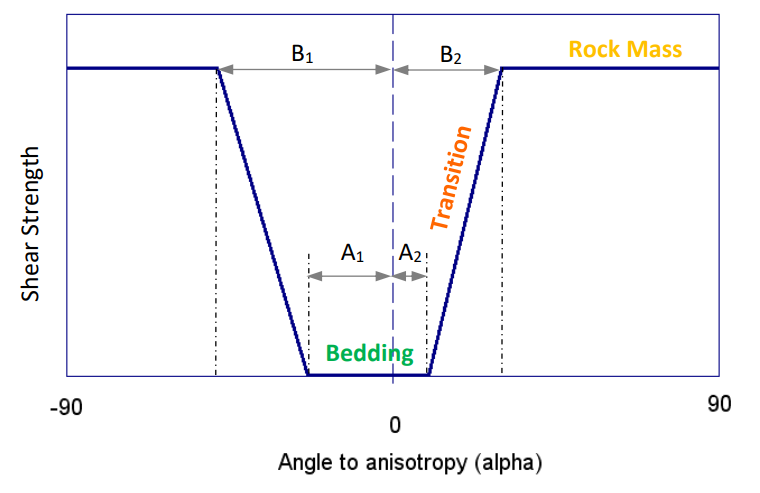
Non-Symmetric anisotropy function for Snowden Modified Anisotropic Linear model
Both the Snowden Modified Anisotropic Linear model and the Anisotropic Linear model assume a linear transition between the bedding plane strength and the rock mass strength. The original Anisotropic Linear model assumes constant values of cohesion and friction angle for the bedding and rock mass. For the Snowden Modified Anisotropic Linear model, non-linear strength functions can be defined for the bedding and rock mass using one of these two options:
1- Shear-Normal function
2- Cohesion-Friction function
Residual shear strength, peak and residual tensile strength are also considered for beddings and the rock mass. There are two methods of defining the direction of the anisotropy:
1- Angle
2- Surface
If the Anisotropy Definition is set to Angle, then the direction of anisotropy is constant and defined by a single angle which is entered in the Angle (ccw to 1) edit box. If the Anisotropy Definition is set to Surface, then the direction of anisotropy can be variable and defined by an Anisotropic Surface.
An Anisotropic Surface is used to determine the local orientation of anisotropy. The orientation for each Gaussian integration point will be the tangent to anisotropic surface at anode on the surface that is closest to the gaussian integration point.
The yield functions in the mutli-yield model use the nonlinear functions defined for rock mass and beddings to calculate equivalent Mohr-Coulomb criteria with instantaneous friction angles and cohesions calculated based on the current stress state. The plastic flow rules take advantage of dilation ratios.
If the A1 and A2 ranges are greater than zero, more joints with the same strength characteristics are populated within these ranges. If the B1 and B2 ranges are greater than zero two more joints will be generated at midpoint of these range on the corresponding side of the main anisotropy orientation.