Anisotropic Linear

The Anisotropic Linear strength model, proposed by Snowden engineering in Australia (Snowden, 2007), allows you to define a material with the following anisotropic strength characteristics:

• Bedding plane cohesion and friction angle (c1 , phi1) defines the minimum shear strength
• Rock mass cohesion and friction angle (c2 , phi2) defines the maximum shear strength
• Angle of bedding plane orientation (theta) from horizontal
• Parameters A and B define a linear transition from bedding plane strength to rock mass strength, with respect to shear plane orientation.

The relationship between shear strength and alpha angle is illustrated in the Figure below:

Symmetric anisotropy function for Anisotropic Linear model

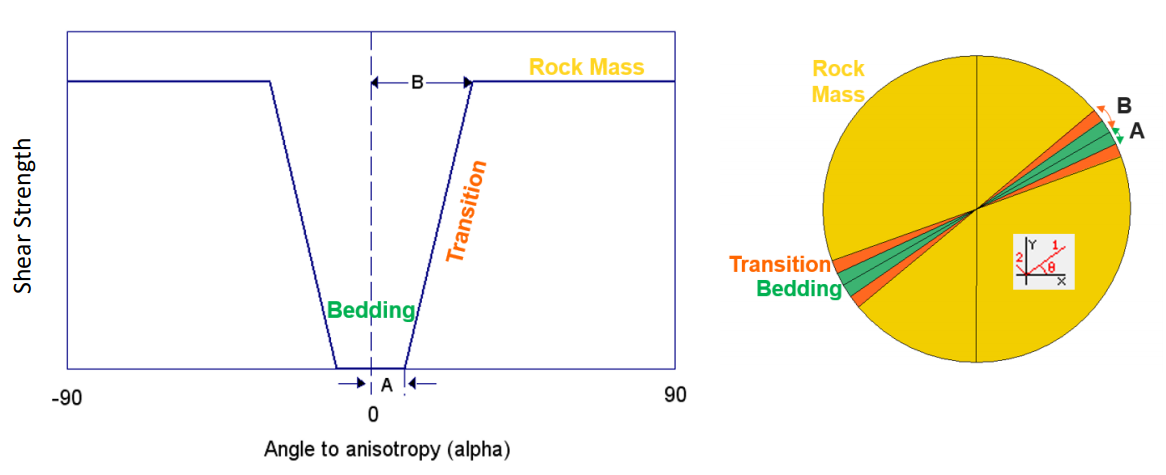
For the Anisotropic Linear strength model there are two methods of defining the direction of the anisotropy:

1- Angle

2- Surface

If the Anisotropy Definition is set to Angle, then the direction of anisotropy is constant and defined by a single angle which is entered in the Angle (ccw to 1) edit box. If the Anisotropy Definition is set to Surface, then the direction of anisotropy can be variable and defined by an Anisotropic Surface.

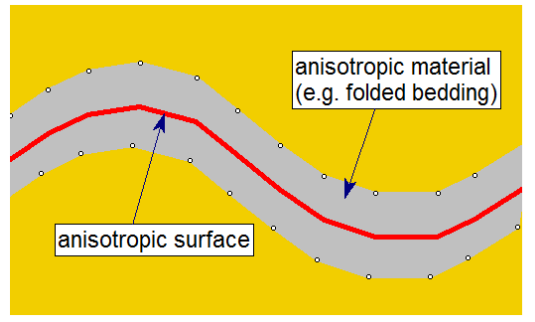
An Anisotropic Surface (See Figure below) is used to determine the local orientation of anisotropy. The orientation for each Gaussian integration point will be the tangent to anisotropic surface at a node on the surface that is closest to the gaussian integration point.

The multi-yield model of the Anisotropic Linear model consists of a matrix that uses a Mohr Coulomb criterion for the rock mass strength and at least a Coulomb joint that takes the bedding strength. If the A range is greater than zero, more joints with the same strength characteristics are populated within this range. If the B range is greater than zero two more joints will be generated at midpoint of this range on both sides of the main anisotropy orientation.

Using the surface option in definition of beddings orientation

The residual values can be considered for the strength of rock mass and beddings. Peak and residual tensile strengths can be applied to the rock mass and beddings. The dilation angle is set to zero for all the mechanisms of this multi-yield model.