Tunnel Lining Design
1.0 Introduction
A circular tunnel of radius 4 m is to be constructed in Schist at a depth of 550m. The in-situ stress field has been measured with the major in-plane principal stress equal to 30 MPa, the minor in-plane principal stress equal to 15 MPa, and the out-of-plane stress equal to 25 MPa. The major principal stress is horizontal, and the minor principal stress is vertical. The strength of the Schist can be represented by the Generalized Hoek-Brown failure criterion with the uniaxial compressive strength of the intact rock equal to 50 MPa, the GSI equal to 50, and mi equal to 10. To compute the rock mass deformation modulus, the modulus ratio (MR) is assumed to be 400. The support is to be installed 2 m from the tunnel face.
The goal of this tutorial is to design a reinforced concrete lining with a factor of safety greater than 1.4.
To design a support system, the following three steps must be performed:
- Determine the amount of tunnel wall deformation prior to support installation. As a tunnel is excavated, there is a certain amount of deformation, usually 35-45% of the final tunnel wall deformation, before the support can be installed. Determining this deformation can be done using either a) observed field values, b) numerically from 3D finite-element models or axisymmetric finite-element models, or c) by using empirical relationships such as those proposed by Panet or Vlachopoulos and Diederichs.
- Using either the internal pressure reduction method, or the modulus reduction method, determine the internal pressure or modulus that yields the amount of tunnel wall deformation at the point of and prior to support installation. This is the value determined in step 1.
- Build a model that relaxes the boundary to the calculated amount in step 2 using either an internal pressure or modulus. Add the support and determine whether a) the tunnel is stable, b) the tunnel wall deformation meets the specified requirements, and c) the tunnel lining meets certain factor of safety requirements. If any of these conditions are not met, choose a different support system and run the analysis again.
The first step is to determine the amount of tunnel wall deformation prior to support installation. For this tutorial, we’ll use the relationship proposed by Vlachopoulos and Diederichs. The Vlachopoulos and Diederichs method is documented in Appendix 1 of the Kersten Lecture by Hoek, Carranza-Torres, Diederichs and Corkum. A copy of this paper can be found on the Rocscience website in Hoek’s Corner.
This method requires that we build a model of the tunnel and determine a) the deformation far from the tunnel face using a simple plane strain analysis, and b) for the same model determine the plastic zone radius.
In this tutorial, start by building a single model that also combines step 2 with step 1. A plane strain model that relaxes an internal pressure on the tunnel boundary from a value equal to the applied in-situ stress to zero will be built. The final stage, with zero internal pressure, will be used to determine the amount of deformation prior to support installation (step 1). The factoring of the applied internal pressure over several stages will be used to determine the pressure that yields the amount of tunnel wall deformation at the point of support installation (step 2). This tutorial focuses on the analysis of results, with and without support installed. For additional resources discussing model construction, see the RS2 user manual on the Rocscience website.
2.0 Compute: Without Support
- Select: File > Recent Folders > Tutorial Folder
- Open Tunnel Lining Design (Initial)
In this initial file, the model has been staged, project settings defined, material properties defined and assigned, and an induced load applied over the stages.
- Select: Analysis > Compute

3.0 Results and Discussion: Without Support
- Select: Analysis > Interpret

The maximum stress, Sigma 1, for Stage 1 will be displayed. Notice that there is no variation of stress and that the stress (30 MPa) is equal to the major in-situ field stress. This means that the internal pressure is equal and opposite to the field stress and the model is behaving as if the tunnel did not exist.
- Click the Zoom Excavation
 button on the toolbar.
button on the toolbar.
- Change the contours to plotTotal Displacement using the pull-down menu in the toolbar. There no displacement visible in the first stage.
- Now click through the stages. There is an increase in deformation around the tunnel as the internal pressure is reduced.
Step 1: Computing tunnel deformation before support installation using the Vlachopoulos and Diederichs method
To compute the tunnel deformation at the point of support installation, the empirical relationship developed by Vlachopoulos and Diederichs will be used. To use this method, two pieces of information are required from the finite-element analysis: a) the maximum tunnel wall displacement far from the tunnel face, and b) the radius of the plastic zone far from the tunnel face.
Both values can be computed from a plane strain analysis with zero internal pressure inside the excavation. In the model, the results from stage 11 are used since there is zero internal pressure in this stage.
Switch to the last stage (stage 11). Look in the lower left corner of the program window on the status bar. The maximum displacement for this stage is approximately 0.0432m. This is the value of maximum wall displacement far from the tunnel face. The location of this displacement is in the roof and floor of the excavation. The location of this displacement is important since any comparisons of displacement for various internal pressures must be made at the same location.
- To determine the radius of the plastic zone, turn on the display of Yielded Elements

Several crosses are displayed and represent elements in the finite element analysis that have failed. - Zoom Out to see the entire extent of failed points is visible (see below).
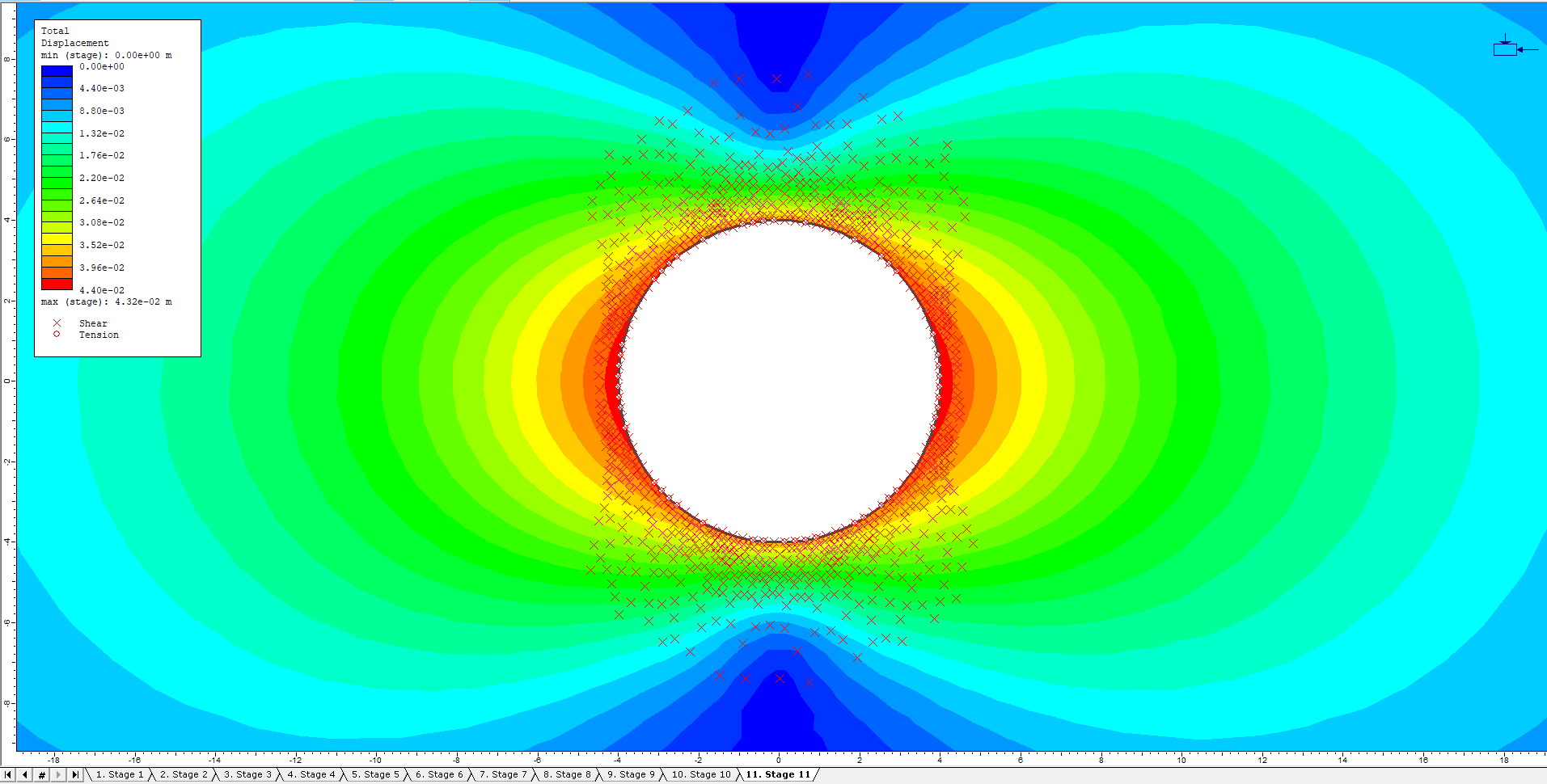
The extent of this failed zone represents the extent of the plastic zone around the tunnel. To determine the radius of the plastic zone, use either the measuring tool or the dimensioning tool to measure the distance from the center of the tunnel to the perimeter of the yielded/plastic zone. Let’s use the measuring tool.
- Select: Tools > Add Tool > Measure
- Set (0,0) as the location to measure from. Use the mouse to extend the measuring line vertically until reaching the edge of the yielded zone. Click the left mouse button.
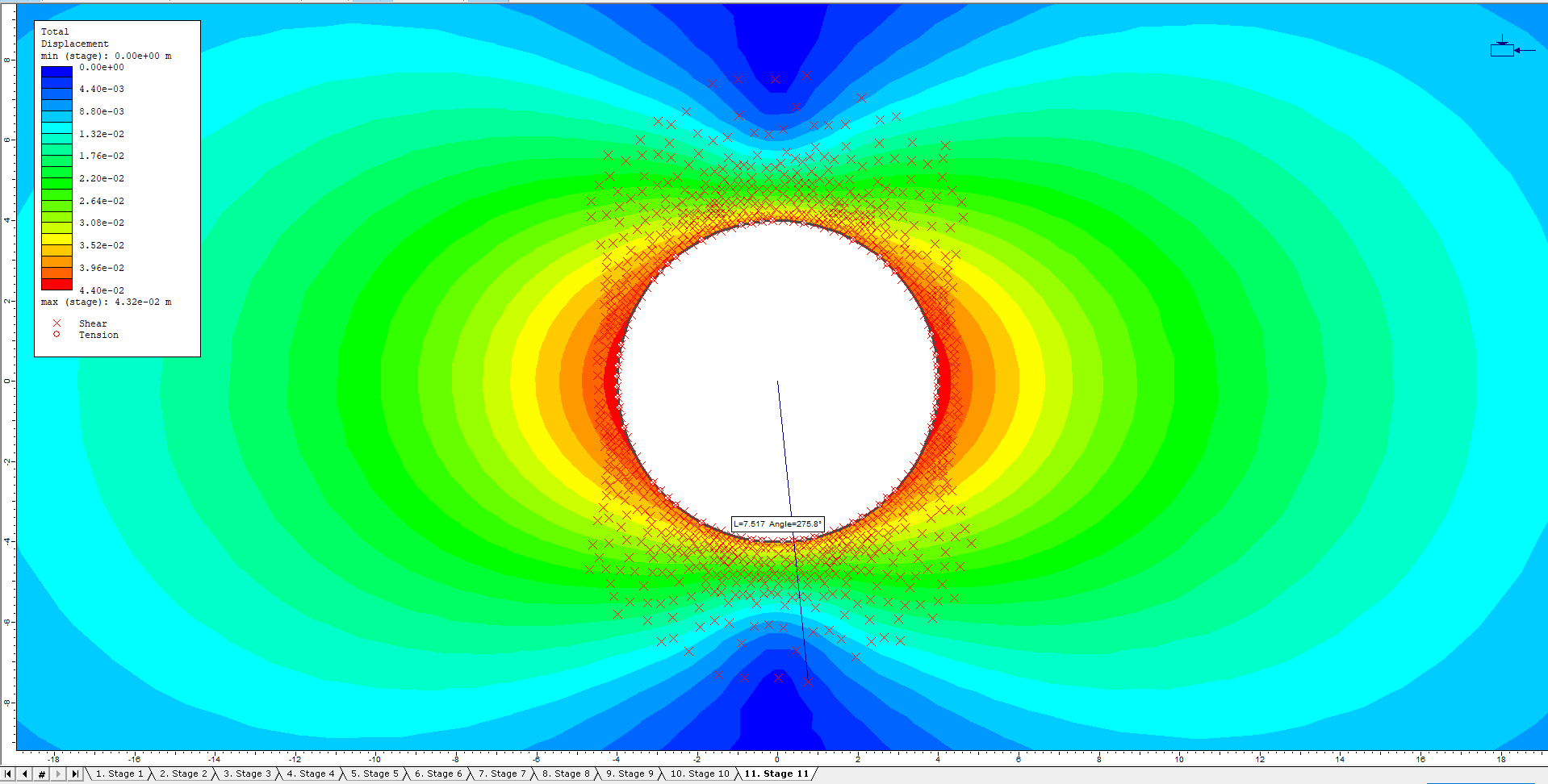
As seen above, the radius of the plastic zone is approximately 7.5m.
Computing displacement prior to support installation using the Vlachopoulos and Diederichs Method
The following plot was created using the Vlachopoulos and Diederichs equations. The equations can be found in the Kersten Lecture, appendix 1. Using this plot, it is possible to estimate the amount of closure prior to support installation, knowing the plastic radius and displacement far from the tunnel face.
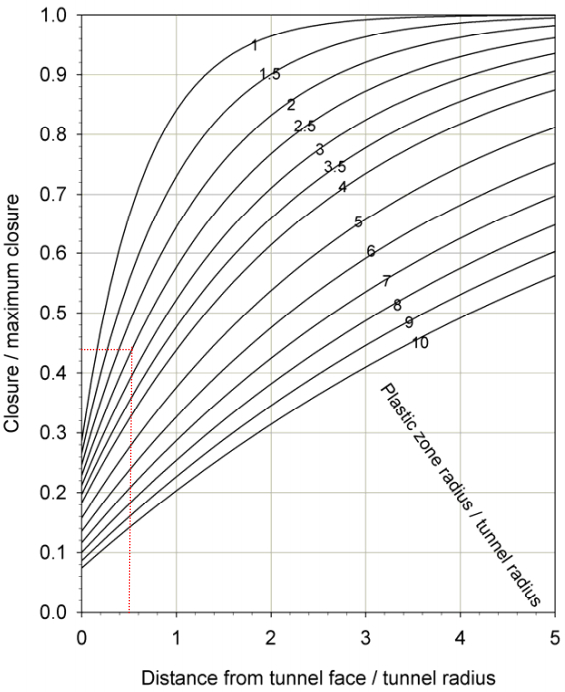
For this problem, Rp=7.5m, Rt=4m, X=2m, and umax=0.043m. The distance from tunnel face/tunnel radius = 2/4 = 0.5. The plastic zone radius/tunnel radius = 7.5/4 = 1.88. From the above plot this gives closure/max closure approximately equal to 0.52. Therefore the closure equals (0.52)*(0.043) = 0.022m.
As computed above, the tunnel roof displaces 0.022m before the support is installed.
Step 2: Determining the internal pressure factor
The next step is to determine the internal pressure that yields a displacement of 0.028m in the roof of the tunnel. It is important to maintain the same location as is used to determine umax, since the location of maximum displacement can change depending on the magnitude of the internal pressure. This can be seen in this model as larger internal pressures produce larger displacement in the sidewall while smaller internal pressures produce larger displacements in the roof and floor.
To determine the internal pressure that yields a 0.028m roof displacement, plot the displacement versus stage for a point on the roof of the excavation.
- Make sure Total Displacement is selected as the data type.
Graphing Displacement in the Roof of the Excavation
To create the graph:
- Select: Graph > Graph Single Point vs. Stage
- Use the drop down menu to select Graph Single Point vs. Stage
- When asked to enter a vertex, type in the value (0,4) for the location and press Enter. This is a point on the roof of the excavation.
- The Graph Query Data dialog will appear. Select Horizontal Axis = Stage Number.
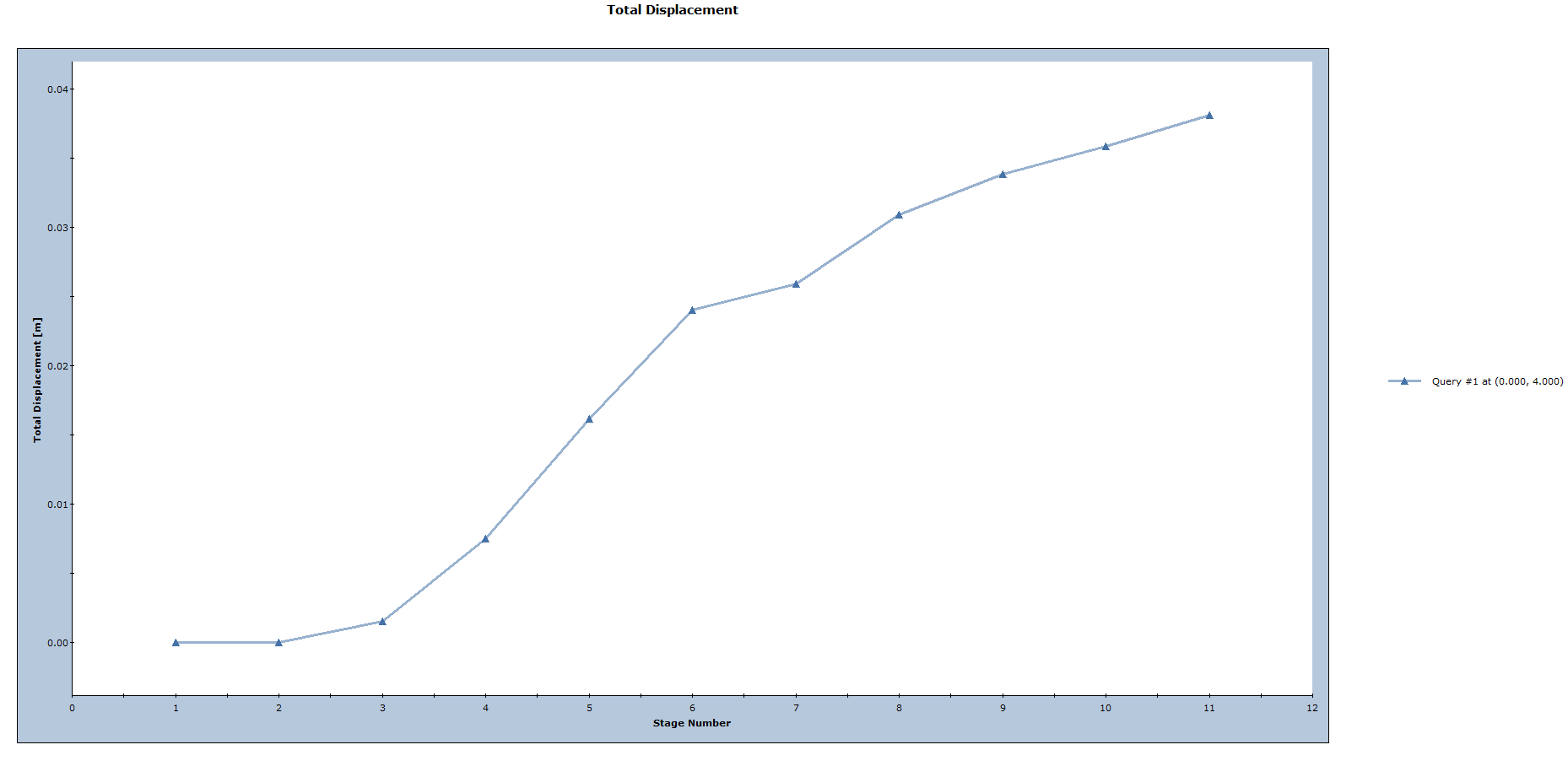
- Click Plot. The following figure shows the plot generated by the program. This is a plot of displacement versus stage for a point in the roof of the tunnel.
- Right-click in the plot and choose the Sampler option. Move the sampler by moving the mouse with the left mouse button. Move the sampler until the displacement value on the right side of the plot is equal to 0.028m.
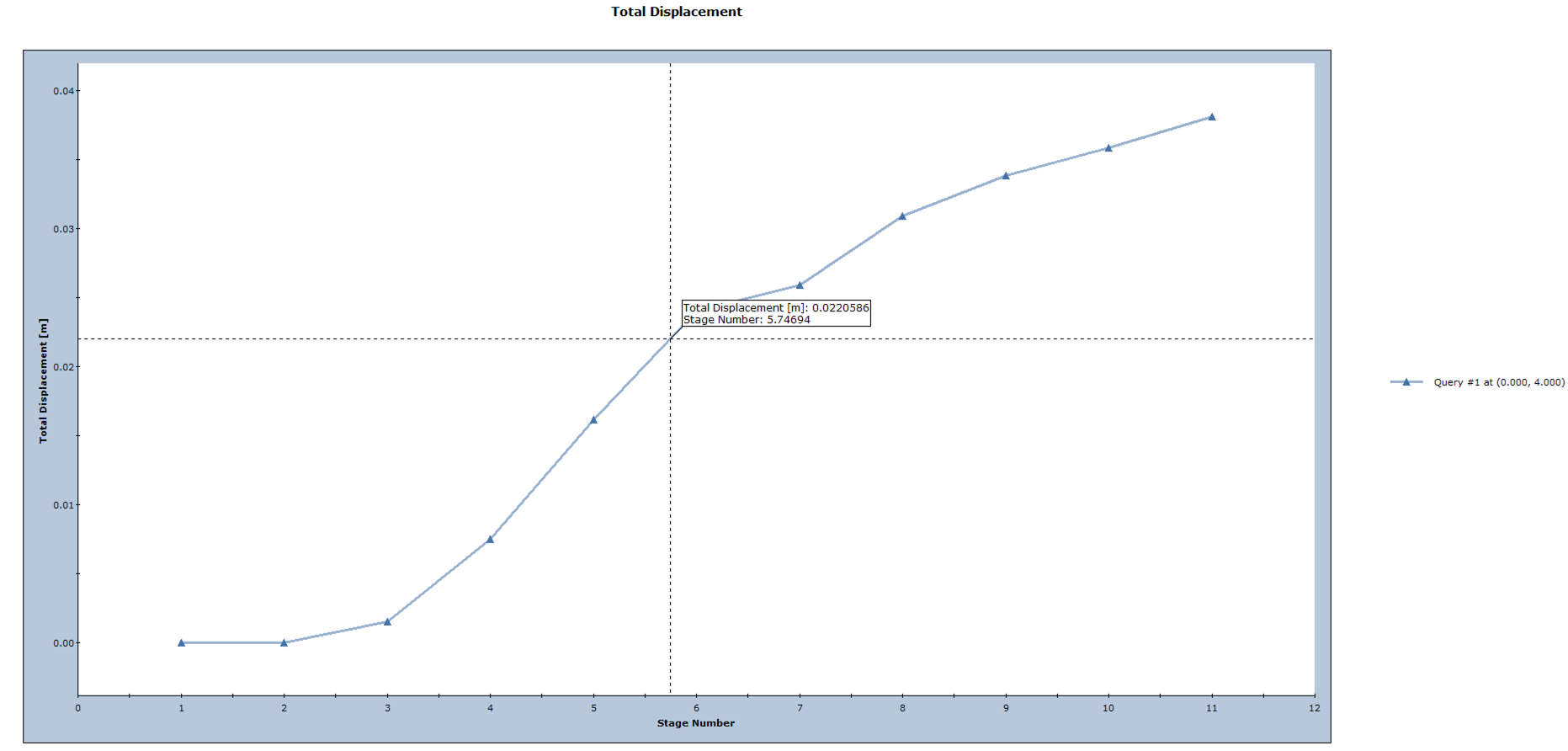
In stage 5, the wall displacement in the roof of the tunnel is 0.022m. This represents an internal pressure factor of 0.2 as was defined in the modeler for the field stress vector distributed load.
Creating a convergence confinement graph in Excel
To create a convergence confinement graph, which plots displacement versus internal pressure, export the above graph to Microsoft Excel.
- Right-click the graph and choose the Plot in Excel option.
Excel will launch with a plot of stage number versus displacement. It is simple to modify the plot to change the stage number data to the internal pressure factor. A sample of the Excel file for this example is included in the Tutorials folder with the RS2 data files.
The following image shows the convergence-confinement plot in Excel for this example. This plot shows that an internal pressure factor of 0.2 yields the tunnel wall displacement computed above for the point of support installation (0.022m).
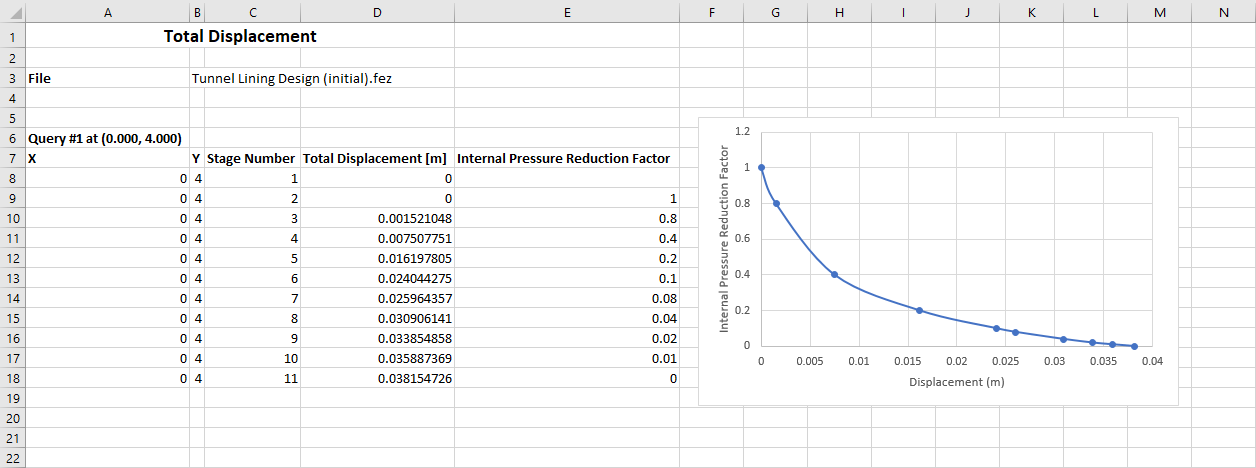
Steps 1 and 2, as defined in the Problem section at the beginning of this tutorial, have now been completed. Let’s analyze the model with a support system included in the design.
- From Interpret, switch back to the RS2 Modeler program by clicking Open Modeler
 in the toolbar (or select Analysis > Modeler).
in the toolbar (or select Analysis > Modeler).
4.0 Model and Compute: With Support
- Open the Project Settings
 dialog from the Analysis menu and select the Stages tab.
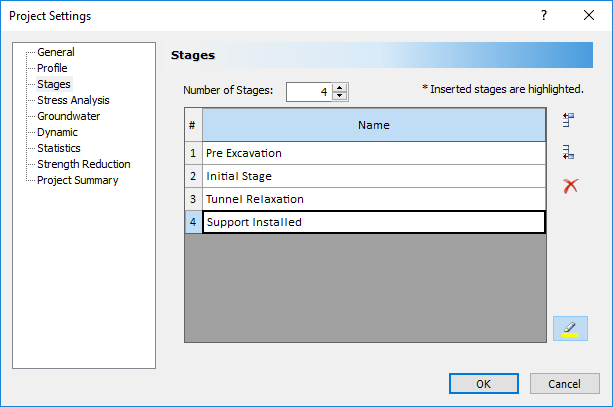
dialog from the Analysis menu and select the Stages tab. - Change the name of:
- Stage 1 to Pre Excavation.
- Stage 2 to Initial Stage.
- Stage 5 to Tunnel Relaxation.
- Stage 11 to Support Installed.
- Now delete all other stages except these four stages. Note, you can select multiple stages by scrolling down the number column with the left mouse button depressed. Use the Delete Stages button to delete the stages. After deleting these stages, the dialog should look like:
- Close the dialog by clicking OK. Make sure the Stage 2 tab is selected.
- Click Zoom Excavation
 in the toolbar.
in the toolbar.
The dialog should look like this:
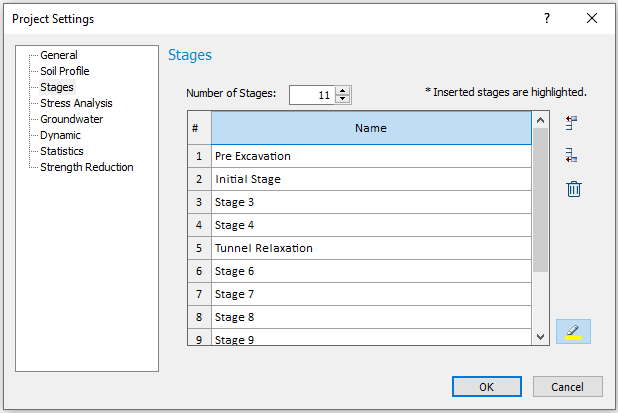
Stage 5 from the previous model was selected because it represents the stage in which the internal pressure in the tunnel yields the necessary deformation before we install the support.

Click through the stages. Stage 3, the tunnel relaxation stage, should look like:

Stage 4, the Support Installed stage, should have no load on the boundary.
SETTING THE REINFORCED CONCRETE LINER PROPERTIES
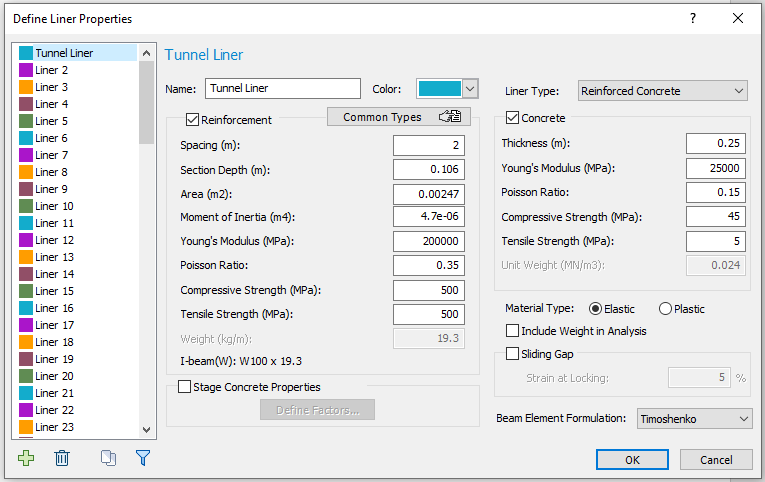
Now define the liner properties. The properties we enter will correspond to a 100 mm thick layer of concrete reinforced with W100X19.3 I-beams spaced at 2 meter intervals along the tunnel axis.
- Select: Properties > Define Liners

- Change the Name of the liner to Tunnel Liner
- Change the Liner Type to Reinforced Concrete
- Click on the Common Types button. You will see the Reinforcement database dialog shown below. For the Reinforcement, select an I-beam from a list of standard reinforcement types.
- In the Reinforcement database dialog, select the W100 x 19.3 I-beam. Click OK, and the I-beam reinforcement properties will be automatically loaded into the Define Liner Properties dialog.
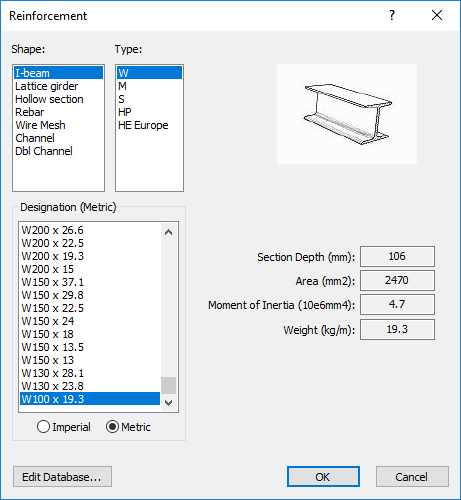
- In the Define Liner Properties dialog, for the Reinforcement, enter a spacing of 2m.
- Enter the properties for the concrete.
- Thickness=0.25m
- Modulus=25000MPa
- Poisson Ratio=0.15
- Compressive Strength=45MPa
- Tensile Strength=5MPa
- Click OK to save your input and exit the dialog.
The liner properties dialog should look like:
ADDING A REINFORCED CONCRETE LINER TO THE TUNNEL
Let's line the tunnel with the liner described above. First, ensure that Stage 4, the Support Installed stage, is selected.
- Select: Support > Add Liner

- Click OK in the Add Liner dialog.
- Click and hold the left mouse button, and drag a selection window which encloses the entire excavation. Release the left mouse button. Notice that all excavation line segments are selected.
- Right-click the mouse and select Done Selection, or just press the Enter key. The entire tunnel will now be lined, as indicated by the thick blue line segments around the excavation boundary (see below).

Click through the stages. Notice how the colour of the liner changes from light blue in stages 1, 2, and 3 to dark blue in stage 4. This indicates that the liner is being installed in stage 4.
The addition of the liner is now complete and it is time to run the analysis.
- Before computing, save the file as Tunnel Lining Design (Part 2)
- Select: Analysis > Compute

5.0 Results and Discussion: With Support
- Select: Analysis > Interpret

- Make sure the Stage 3 tab is selected.
- Click the Zoom Excavation
 button in the toolbar.
button in the toolbar.
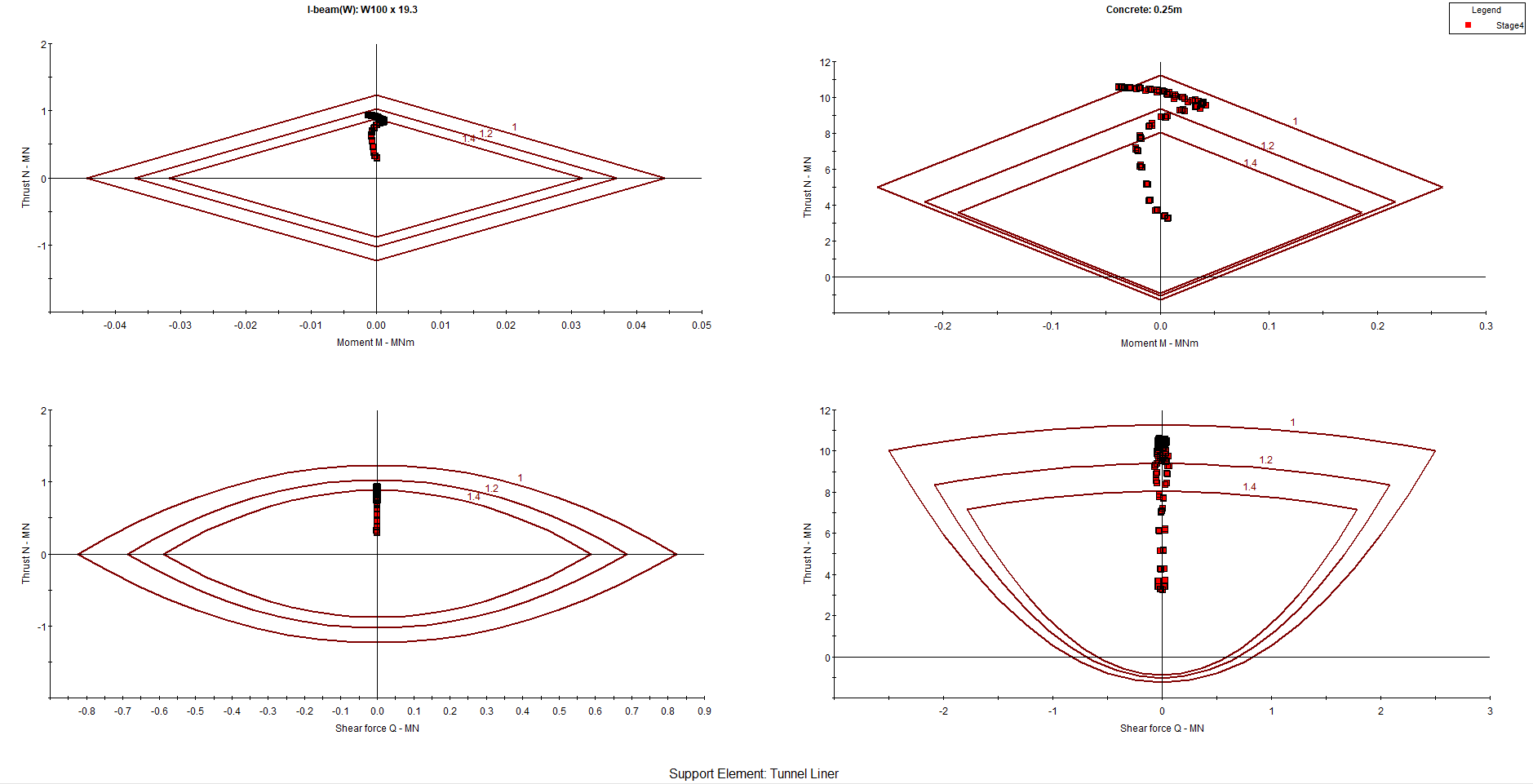
5.1 Support Capacity Diagrams
Support capacity diagrams give the engineer a method for determining the factor of safety of a reinforced concrete liner. For a given factor of safety, capacity envelopes are plotted in axial force versus moment space and axial force versus shear force space. Values of axial force, and moment and shear force for the liner are then compared to the capacity envelopes. If the computed liner values fall inside an envelope, they have a factor of safety greater than the envelope value. So, if all the computed liner values fall inside the design factor of safety capacity envelope, the factor of safety of the liner exceeds the design factor of safety.
- Select: Graph > Support Capacity Plots

The Support Capacity Plot dialog allows the user to choose the support element (i.e. liner type), the number of envelopes, and the stages from which the liner data is taken. - Increase the Number of Envelopes to 3. The dialog should look like:
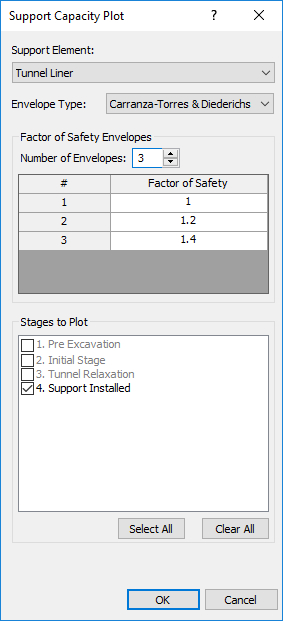
- Press OK.
The following plot is generated. The dark red lines represent the capacity envelopes for the 3 factors of safety (1, 1.2, 1.4). Notice the number of liner data points that fall outside the 1.4 design factor of safety envelope, meaning they have a factor of safety less than 1.4. This occurs for both the capacity diagrams for the concrete and the capacity diagrams for the I-beam. In fact, several points fall outside the factor of safety=1.0 envelope. This liner would most likely experience cracking and crushing if used in this tunnel. This design is improved on further in this tutorial.
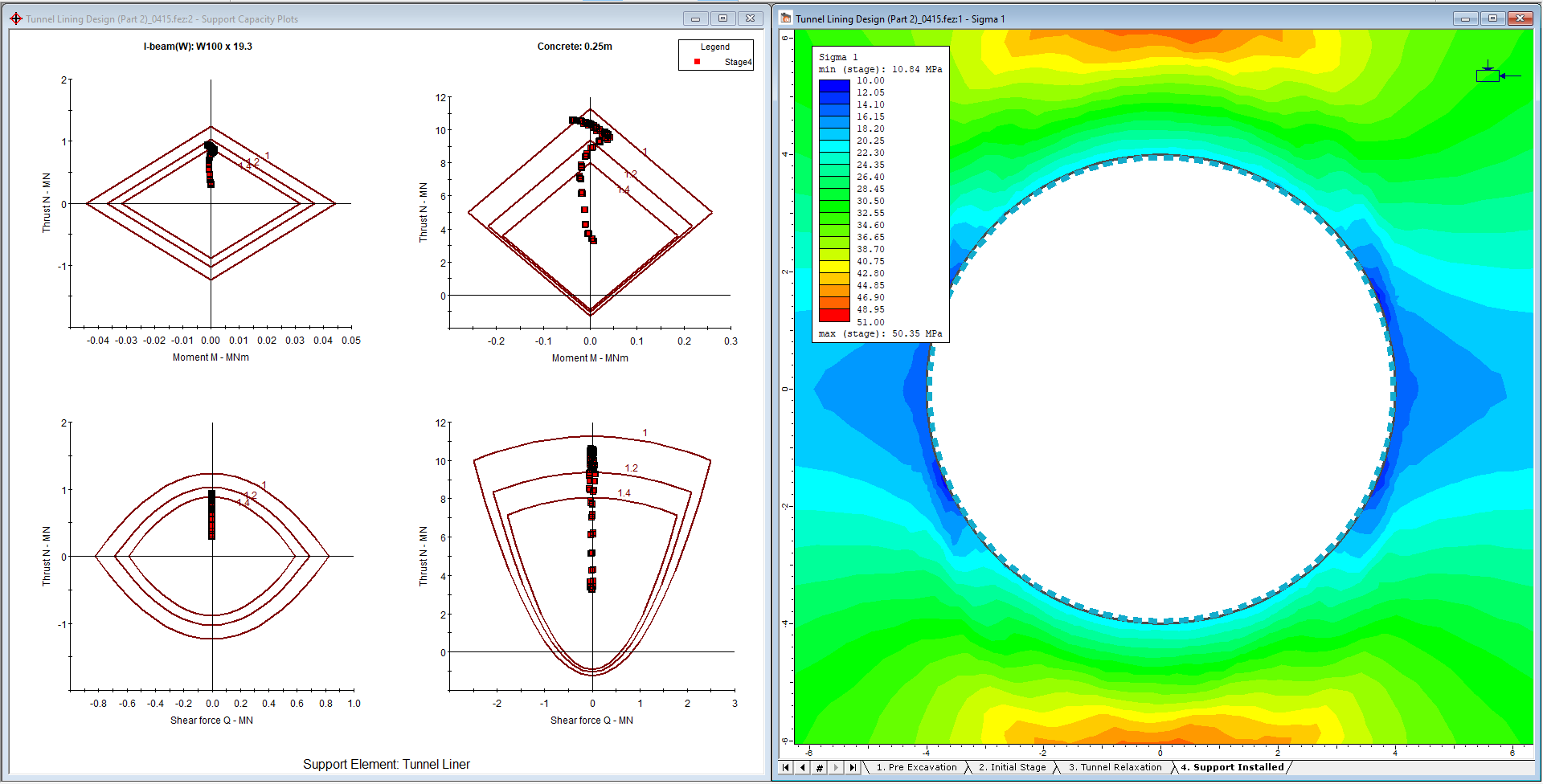
Let’s investigate some of the things you can do with the support capacity envelopes.
- Select: Window > Tile Vertically

- Make sure the Support Capacity Plot view is selected, not the contour view of the tunnel.
To focus on just the concrete moment capacity plot, it can be expanded using the following option. - Select: View > Concrete Moment Capacity Plot
The four plots are replaced by a single plot of the moment capacity for the concrete. Alternatively, it is possible to maximize any single plot interactively by double-clicking on the plot. Double-clicking on the moment capacity for the concrete returns to the four plots. Right-clicking also gives you a context menu that enables you to choose viewing options.
- Ensure that a single plot of the moment capacity for the concrete. The display should look like:
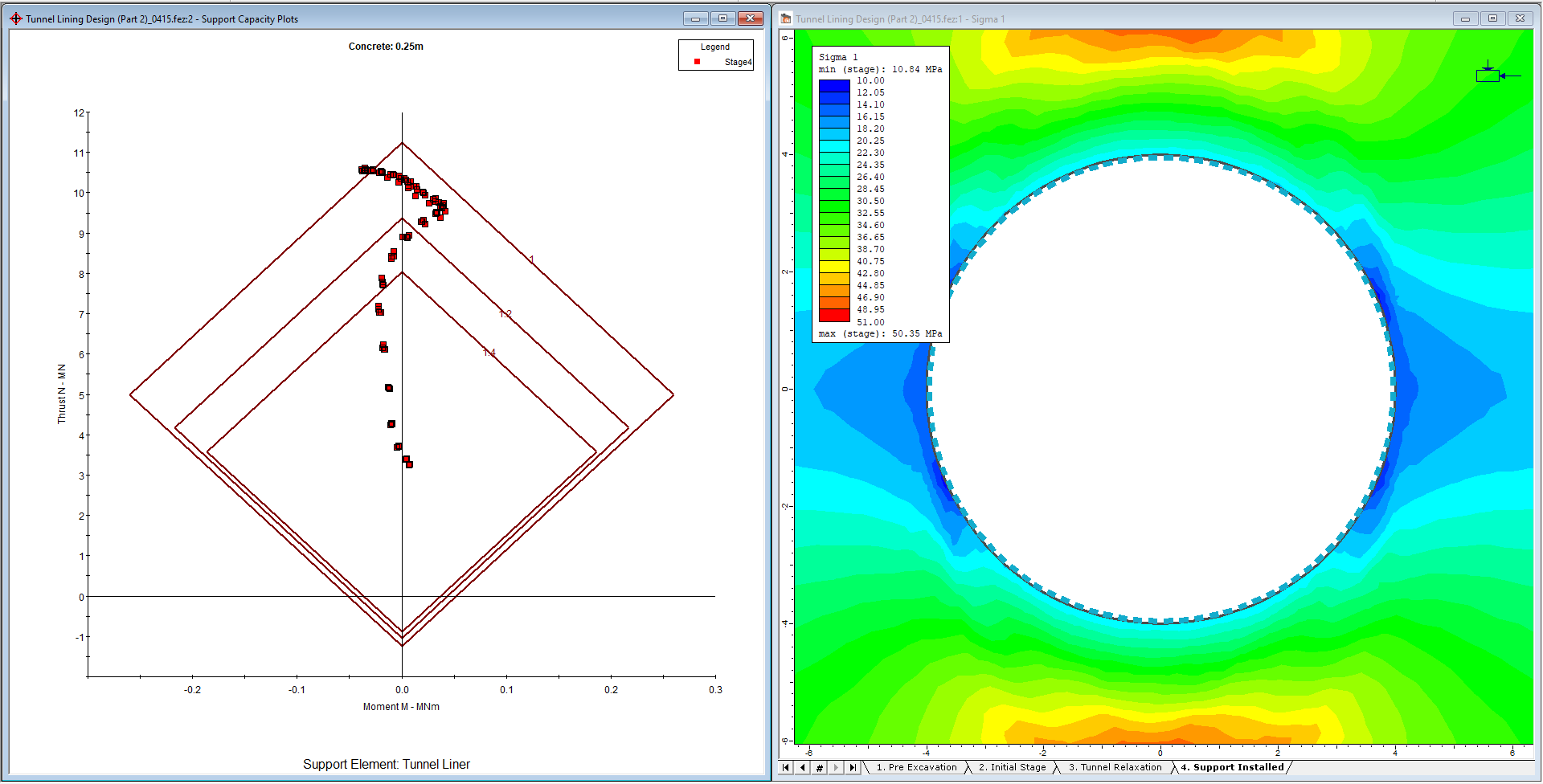
- Select: View > Zoom > Zoom Support Capacity Data
The view is zoomed so that the extents of the plot are determined by the extents of the moment and axial force data for the concrete. - Select: View > Zoom > Zoom All
The plot is returned to the default extents. A mouse wheel can be used to zoom in and out on the data. Holding down the mouse wheel and moving the mouse results in panning of the plot. There are several options for manipulating the plot. Return to the default extents.
- Select: View > Zoom > Zoom All
- Right-click in the plot view and choose the Chart Properties option.
- A dialog containing options for changing the format of the plots is displayed. Close this dialog.
- Now use the mouse to click on one of the red liner data points.
The data point is highlighted in the support capacity plot view and the liner associated with this data is highlighted in the main contour view. This is shown in the following figure.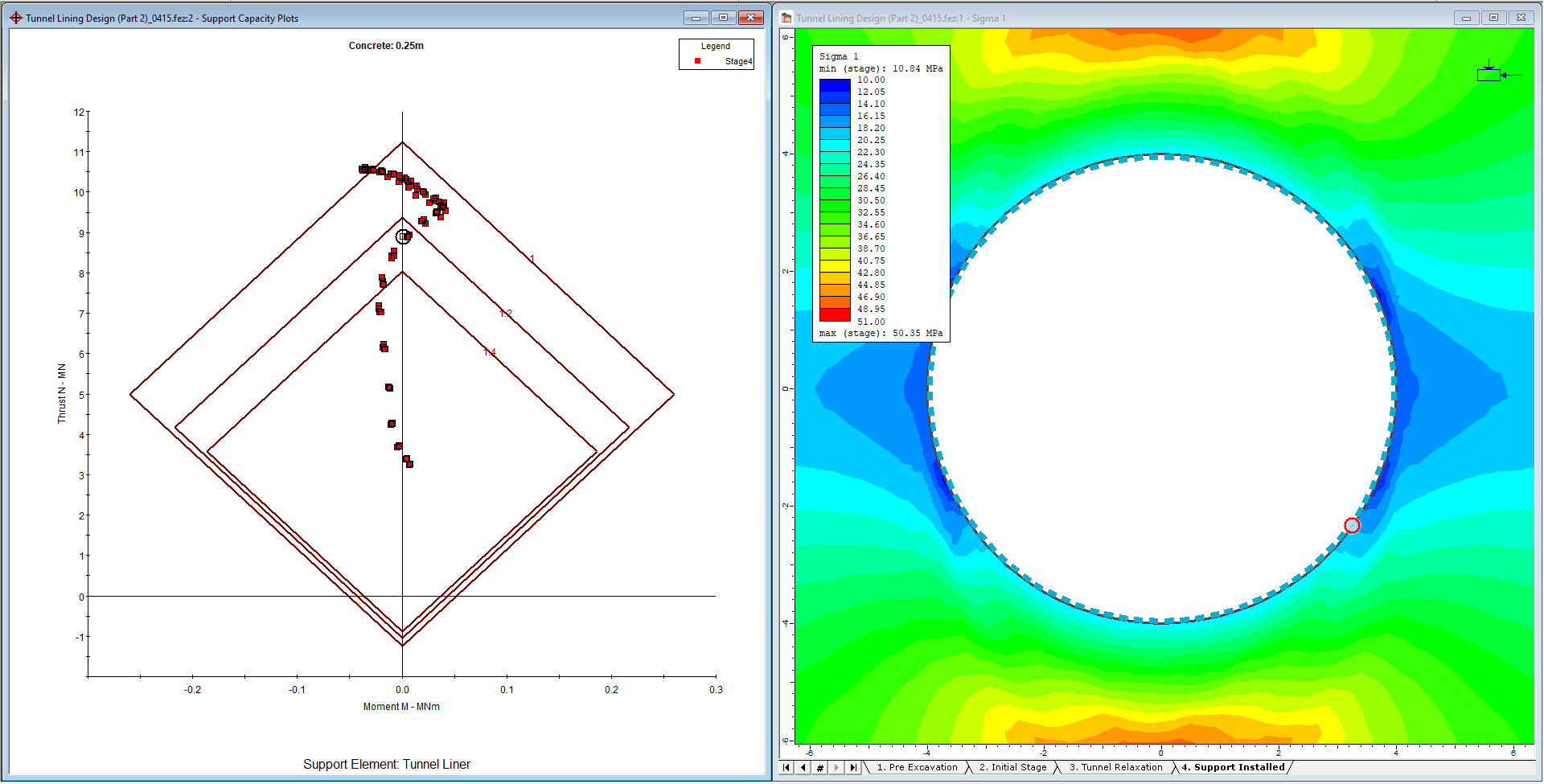
- Right-click in the support capacity plot view and select Filter Data by FS option. The following dialog is displayed. Change the Factor of safety used for filtering to Concrete moment. Change the Maximum value to 1 and turn on the Highlight filtered liners. What this does is plot all the data points with factor of safety between 0 and 1 for the concrete moment and show the associated liner elements in the contour view.

- Press the OK button after making these changes.
In the following image, only the liner elements with factor of safety between 0 and 1 for the concrete are displayed. The liner elements associated with these data points are highlighted on the contour view by drawing a grey circle around each element. The areas of minimum factor of safety for the concrete are in the roof and floor of the excavation.
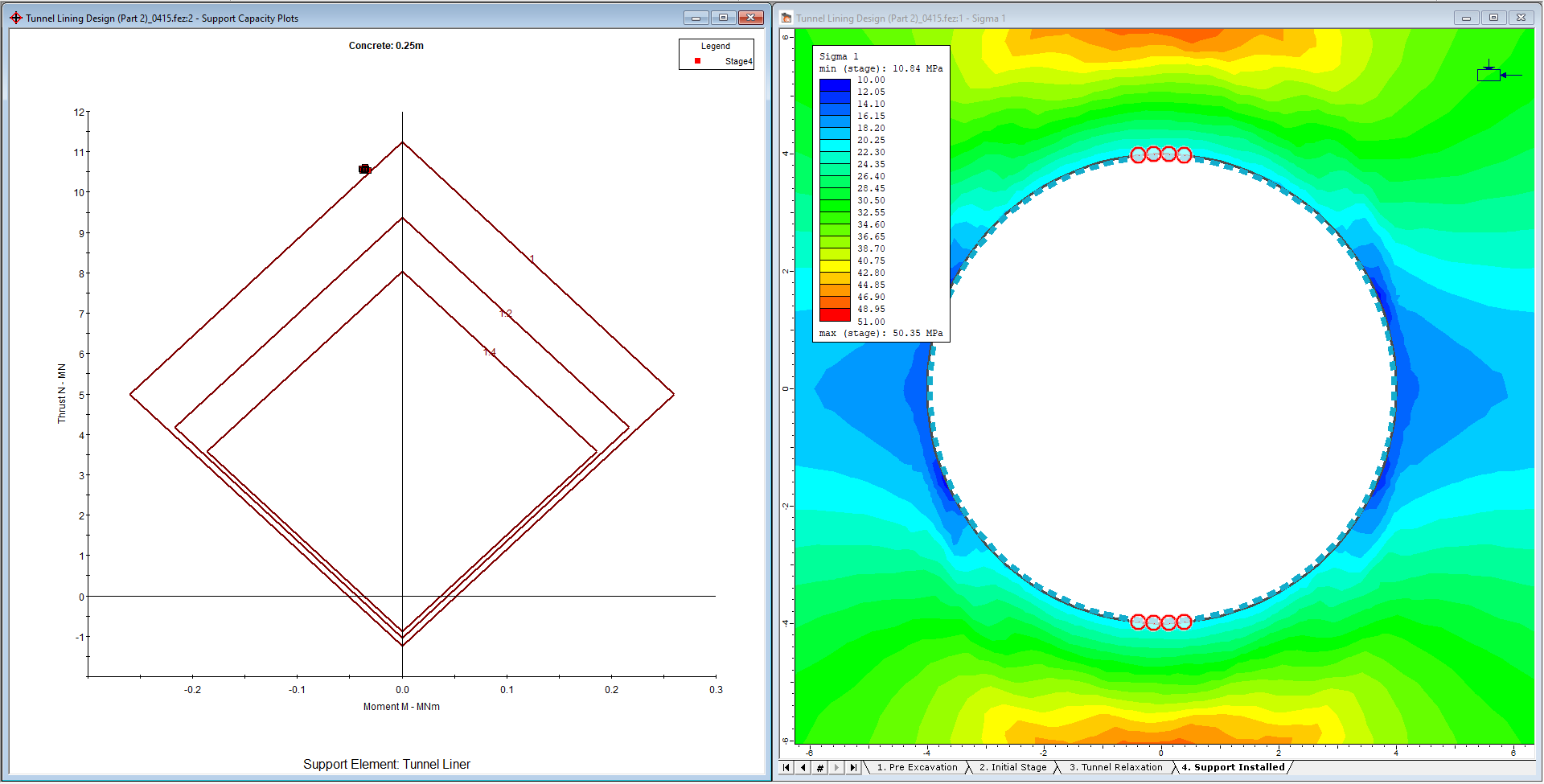
Let’s edit the model to use an improved support system.
6.0 Improving the Support System
- From Interpret, switch back to the RS2 Model
 program.
program. - Select: Properties > Define Liners

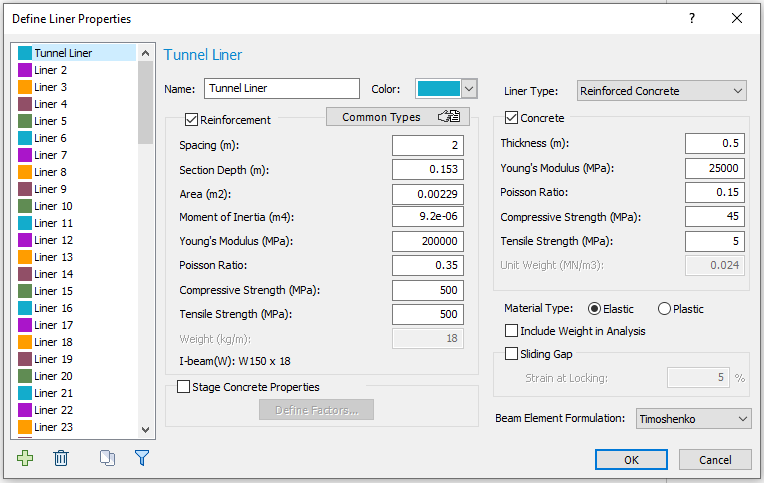
- Make sure the Tunnel Liner tab is selected. Click on the Common Types button.
- In the Reinforcement dialog, select W150 x 18 I-beam. Click OK.
- Increase the thickness of the concrete to 0.5m. The liner properties dialog should look like:
7.0 Compute: With Improved Support
Save the updated model as a new file called Tunnel Lining Design (Part 3).fez. (Make sure you select Save As and not Save, or you will overwrite the LinerDesign.fez file).
- Select: File > Save As

- Save the file as Tunnel Lining Design (Part 3).fez.
- Select: Analysis > Compute

8.0 Results and Discussion: With Improved Support
- Select: Analysis > Interpret

- Select: Graph > Support Capacity Plots

- Increase the Number of Envelopes to 3.
- Click OK.
The following plot is generated:
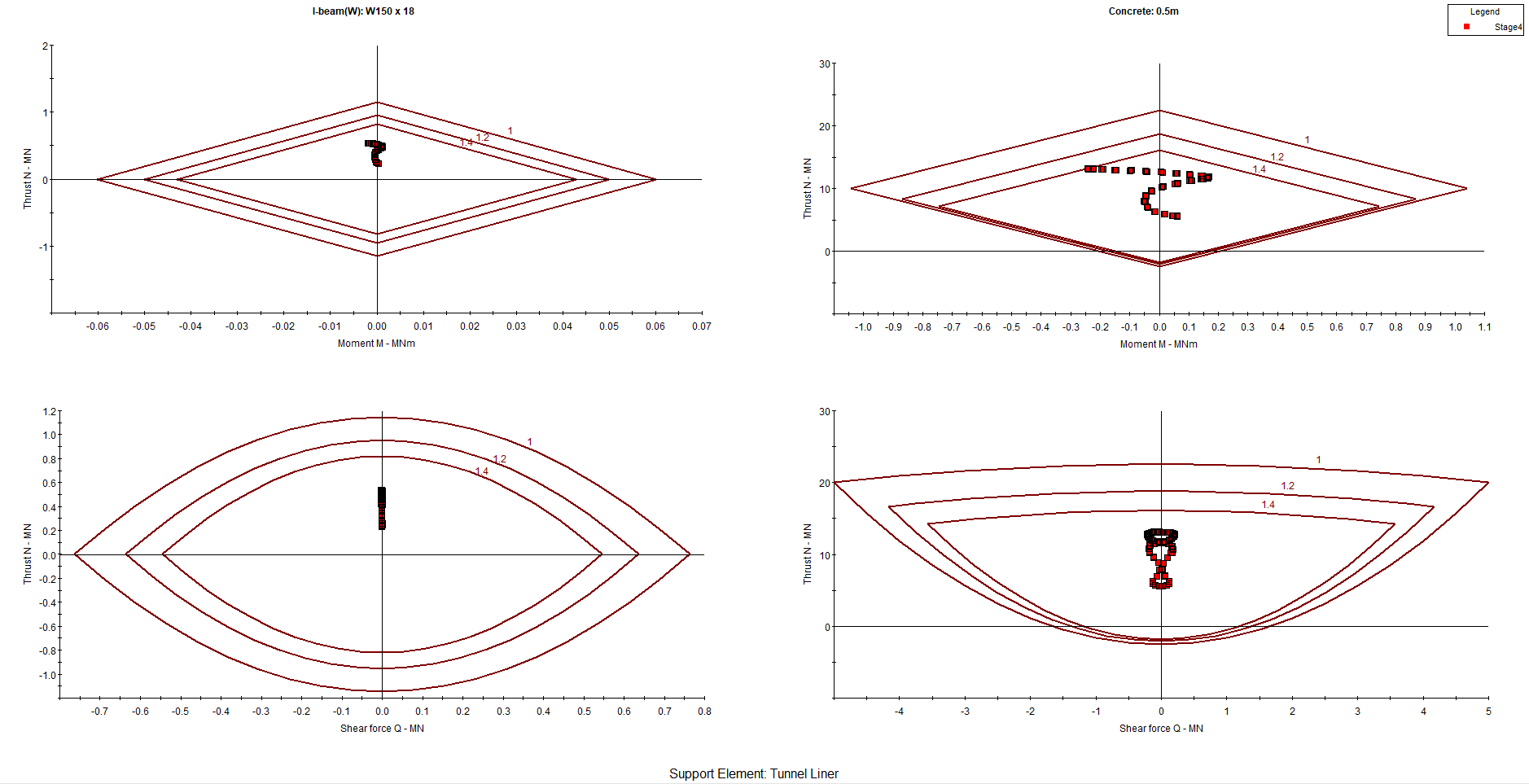
All the data points now fall within the factor of safety =1.4 envelope, on all four plots. This means that the support system chosen has a factor of safety greater than 1.4 thus achieving the design factor of safety.
This concludes the Tunnel Lining Design tutorial.