Random Variables
In order to carry out a Probabilistic Analysis with RS2, you must define at least one input parameter as a random variable.
Random variables are selected and defined using the following options in the Statistics menu.
NOTE: future versions of RS2 may allow additional random variables.
To define an input parameter as a random variable, choose the variable and enter the required statistical parameters (e.g. distribution, mean, standard deviation, minimum and maximum values). For information about the selection of statistical distributions, standard deviation and minimum/maximum values, see the Statistical Distributions Overview topic.
How are the Random Variables used in the Analysis?
Depending on the Sampling Method (Monte Carlo, Latin Hypercube, Point Estimate) the random variables are used as follows.
Monte Carlo or Latin Hypercube sampling
For Monte Carlo or Latin Hypercube sampling, each input parameter that is defined as a random variable is sampled according to the statistical distribution you have defined for the variable, the Sampling Method and the Number of Samples (chosen in Project Settings). This generates N values of each random variable (where N = Number of Samples).
As shown in the following diagram, each iteration of the Probabilistic Analysis is carried out by loading a new set of random variable samples, and re-running the analysis. This is repeated N times where N = Number of Samples.
Random Variable Samples used for Monte Carlo or Latin Hypercube Probabilistic Analysis
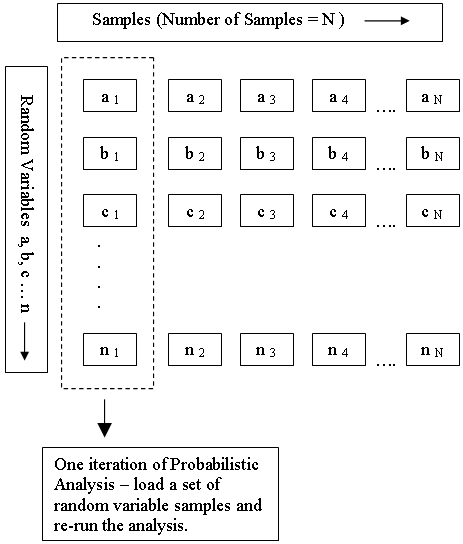
To carry out a Probabilistic Analysis, at least one input parameter must be defined as random.
Point Estimate Method
For the Point Estimate Method, two "point estimates" are made for each random variable at fixed values of one standard deviation on either side of the mean (mean + standard deviation, mean - standard deviation). The finite element analysis is carried out for each possible combination of point estimates. This produces 2m solutions, where m is the number of random variables involved.
Example
Let's say you wanted to account for the uncertainty in the material strength parameters cohesion and friction angle for a single material.
Number of random variables = 2 (cohesion and friction angle).
Mean value of cohesion = 5 with standard deviation = 1. Point estimates = 4 and 6 (i.e. 5 plus / minus 1)
Mean value of friction angle = 25 with standard deviation = 2. Point estimates = 23 and 27 (i.e. 25 plus / minus 2).
There are four possible combinations of point estimates:
Cohesion | Friction Angle |
4 | 23 |
4 | 27 |
6 | 23 |
6 | 27 |
When you select Compute, the finite element analysis will be computed independently for each possible combination of random variable point estimates. In this example, the finite element analysis would be computed FOUR times (once for each of the four combinations of point estimates for c and phi.) In addition, the RS2 analysis is always computed ONCE using the mean values of all parameters (i.e. the same as a deterministic finite element analysis). So the analysis would be run a total of FIVE times for this case.
For additional information regarding the applicability and theoretical background of the point estimate method see the Probabilistic Analysis document in the RS2 theory section.
Monte Carlo / Latin Hypercube versus Point Estimate Method
In general the Monte Carlo or Latin Hypercube methods are recommended, since you can define the Number of Samples directly, and you can choose from a wide variety of statistical distributions for each variable.
In the context of RS2 finite element analysis, the Rosenblueth point estimate method of probabilistic analysis is suitable for problems involving only a few random variables (e.g. 2 to 6). For larger numbers of random variables (e.g. greater than 10) the computation time and output file storage requirements may become prohibitive, since the number of analyses required is 2m (where m is the number of random variables). For example 10 random variables would require 210 = 1024 separate finite element analyses, which could take several hours of computation time, depending on the speed of your computer and the size and nature of the problem being computed. This is one of the drawbacks of the point estimate method -- the number of analyses required is exponential with respect to the number of random variables.
For problems involving more than about 10 random variables, the Monte Carlo or Latin Hypercube methods are recommended.