Elastic Properties
The following elastic models are available for defining your material elastic properties in the Define Material Properties dialog:
- Isotropic
- Transversely Isotropic
- Orthotropic
- Duncan-Chang Hyperbolic
- Non-linear Isotropic
- Visco-Elastic
Isotropic
An Isotropic material implies that the material properties do not vary with direction. The elastic properties of an Isotropic material are defined by a single value of Young’s Modulus and a single value of Poisson’s Ratio.
Residual Young's Modulus
For an Isotropic material you can define a residual value of Young's Modulus by selecting the Young's Modulus (residual) check box. This option is only enabled if the Material Type = Plastic and the failure criterion = Mohr-Coulomb, Hoek-Brown or Drucker-Prager. The residual value of Young's Modulus will be used in the analysis under the following conditions:
- Material yielding has occurred (peak strength envelope exceeded)
- After yielding, the material is subjected to a change in load state (i.e. unloading / reloading).
Only under these conditions will the residual modulus be applied. If the material yields but the load state does not change, then the residual modulus will not be applied. This is indicated in the following figure.
Definition of residual Young's modulus
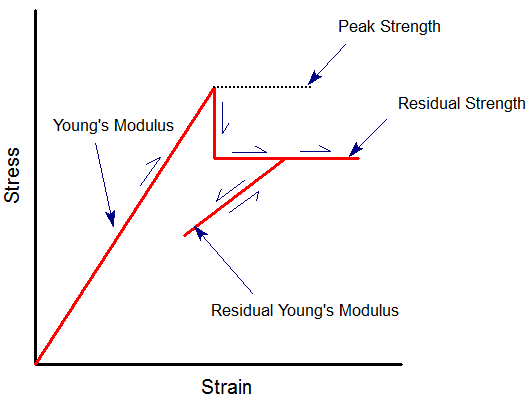
Note: RS2 assumes an abrupt drop from peak to residual strength after failure (i.e. strain softening is not considered). Therefore the residual modulus is NOT the slope of the strain softening curve, since strain softening is not considered.
Transversely Isotropic
A Transversely Isotropic material has properties which vary with direction. The elastic properties are specified in two orthogonal directions as follows:
- E1 and E2 are the in-plane elastic moduli.
- Ez (the out-of-plane elastic modulus) is assumed to be equal to E1.
- The required Poisson’s ratios are n12 and n1z = nz1 = n. Note that nij implies strain in the j-direction due to strain in the i-direction. Also note that Ei / Ej = nij / nji. Therefore, the plane 1-Z is the isotropic plane
- G12 is the in-plane shear modulus
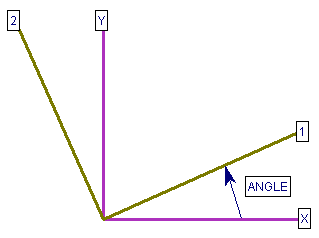
- The Angle is measured between the x-direction and the direction of E1, as shown in the figure below.
Definition of Angle for Transversely Isotropic or Orthotropic materials
Orthotropic
An Orthotropic material has properties which vary with direction. The elastic properties are specified in THREE orthogonal directions.
For an Orthotropic material three Young's moduli are required - E1, E2 and Ez - where the out-of-plane elastic modulus Ez is no longer equal to E1. Three separate Poisson’s ratios are also required, n12, n1z and n2z. The in-plane shear modulus G12 and the Angle definition are the same as for a Transversely Isotropic material.
Duncan-Chang Hyperbolic
The Duncan-Chang Hyperbolic constitutive model [ Duncan and Chang, (1970) ] is widely used for the modeling of soil behaviour, and is capable of modeling the non-linear, stress-dependent and inelastic behaviour of cohesive and cohesionless soils.
The Duncan-Chang Hyperbolic model can only be used in conjunction with the Mohr-Coulomb failure criterion in RS2.
The following input parameters are used to define the Duncan-Chang Hyperbolic model in RS2:
Modulus Number (Ke) - this dimensionless parameter represents Young's modulus (range of values: 350-1120)
Modulus Exponent (n) - governs the stress dependence of Ke on sigma3 (range of values: 0-1)
Unloading Modulus Number (Ku) - is used to calculate the tangential modulus for unloading/reloading conditions
Failure Ratio (Rf) - defines the shape of the stress-strain curve (range of values: 0.60-0.95)
Atmospheric Pressure (Patm) - used for normalization of stress input
Poisson's Ratio (v) - can be specified as either Constant or Stress Dependent.
- If Poisson's Ratio = Constant, then Poisson's Ratio is entered directly as a constant value.
- If Poisson's Ratio = Stress Dependent, then the Bulk Modulus parameters are entered (see below).
Bulk Modulus Number (Kb) - this dimensionless parameter characterizes the volumetric change (range of values: 200-700)
Bulk Modulus Exponent (m) - governs the stress dependence of Kb on sigma3 (range of values: 0-1)
Based on a hyperbolic stress-strain curve and stress-dependent material properties, the following equations are derived [ Duncan and Chang, (1970) ] for the Duncan-Chang Hyperbolic model.
The tangential modulus (Et) for a given stress condition, is given by Eqn.1.
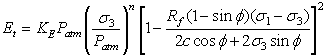 Eqn.1
Eqn.1
The tangential bulk modulus (Bt) and tangential Poisson's ratio are given by Eqn.2 and Eqn.3 respectively.
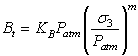 Eqn.2
Eqn.2
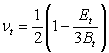 Eqn.3
Eqn.3
Non-linear Isotropic
Non-linear isotropic materials can now be modeled using one of three different non-linear elastic models. For more information about non-linear isotropic models, see the RS2 Elastic Models theory document.
Custom
A Custom option allows users to define their own elastic property model. Tabular values of Young’s Modulus and Poisson’s Ratio can be specified with respect to the chosen Custom Mode. There are six Custom Mode options available:
- Custom P - mean effective stress
- Custom q - scalar deviatoric stress
- Custom S3 - min effective principal stress
- Custom u - pore pressure
- Custom EpsV - volumetric strain
- Custom Gamma - scalar deviatoric strain
The custom stiffness function provides flexibility when none of the predefined models satisfy your needs. In practice, users often assume stiffness behavior based on laboratory testing or fit a known formula to measured data.
If you plan to input lab test data into a custom stiffness function, we recommend first testing it in a single-element model to confirm that the behavior matches expectations before applying it in a more complex analysis. For a typical example of simulating a triaxial test, please see: RS2 Constitutive Model Verification.
Visco-Elastic
Viscoelastic material exhibit both elastic and viscous behaviours when stress applied. The elasticity results in an instantaneous strain, and the viscosity results in a time-dependent strain rate.
The Visco-Elastic model is available to select only when the Apply Viscous Properties option is checked under the Solver Options page in the Project Settings dialog. In addition, the stage time needs to be specified under the Stages page in the Project Setting dialog.
Three types of Visco-Elastic models are available in RS2: Maxwell, Burgers, and Standard. Each model is described below.
The Maxwell Model consists of a linear elastic spring and a linear viscous dashpot. Required parameters include the elastic bulk modulus (K), Maxwell shear modulus (GM), and Maxwell viscosity parameter (ηM).
The Burgers Model consists of a Maxwell unit and a Kelvin unit. Required parameters include the elastic bulk modulus (K), Maxwell shear modulus (GM), Maxwell viscosity parameter (ηM), Kelvin shear modulus (GK), and Kelvin viscosity parameter (ηK).
The Standard Model consists of a linear elastic spring and a Kelvin unit. Required parameters include the elastic bulk modulus (K), elastic shear modulus (G), Kelvin shear modulus (GK), and Kelvin viscosity parameter (ηK).
For more information about Visco-Elastic models, see the RS2 Elastic Models theory document