4 - Vrakas and Anagnostou Method
1.0 Introduction
This problem was taken from Vrakas and Anagnostou (2014). It compares the results of finite-strain and infinitesimal solutions for tunnel convergence for a problem with a significant final wall displacement. The problem uses material properties corresponding to the Sedrun section of the Gotthard Base Tunnel in Switzerland, which passes through heavily squeezing ground.
This problem will compare Vrakas and Anagnostou’s finite strain method with the Duncan-Fama classical small-strain solution.
Topics covered in this tutorial:
- Duncan-Fama Method
- Vrakas and Anagnostou Method
- Deterministic Analysis
- Custom Support
Finished Product:
The finished product of this tutorial can be found in the Tutorial 04 Using the Vrakas and Anagnostou Method.rsp file, located in the Examples > Tutorials folder in your RocSupport installation folder.
1.1 Run RocSupport
If you have not already done so, run RocSupport by double-clicking on the RocSupport icon in your installation folder. Or from the Start menu, select Programs > Rocscience > RocSupport > RocSupport.
If the RocSupport application window is not already maximized, maximize it now, so that the full screen is available for viewing the model.
2.0 Method 1: Duncan-Fama
We begin by creating a new model:
- Select: File > New

2.1 Project Settings
We will start by studying the Duncan-Fama solution method.
- Select: Analysis > Project Settings

- In the General tab, change the Solution Method to Duncan-Fama (1993). Notice the text on the right updates to give a small description of the small strain method. We will assume all input values are exact values (deterministic).
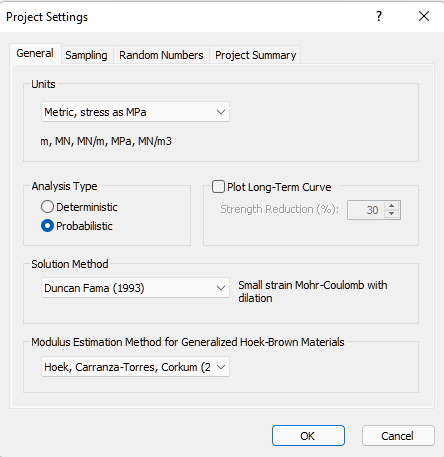
- Click OK.
2.2 Tunnel and Rock Parameters
To open the Tunnel and Rock Parameters dialog:
- Select: Analysis > Tunnel Parameters

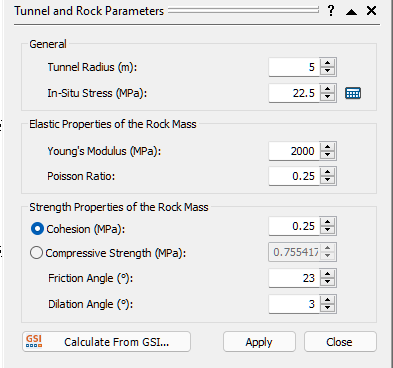
- Enter the following data into the dialog:
- Tunnel Radius = 5 m
- In-Situ Stress = 22.5 MPa
- Young’s Modulus = 2000.00 MPa
- Poisson’s Ratio = 0.25
- Cohesion = 0.25 MPa
- Friction Angle = 23 degrees
- Dilation Angle = 3 degree
- Select Apply and then Close.
- Switch to the Tunnel Section View
 from the toolbar or the Analysis menu.
from the toolbar or the Analysis menu.
The dialog should look as follows:
Your screen should look as follows.
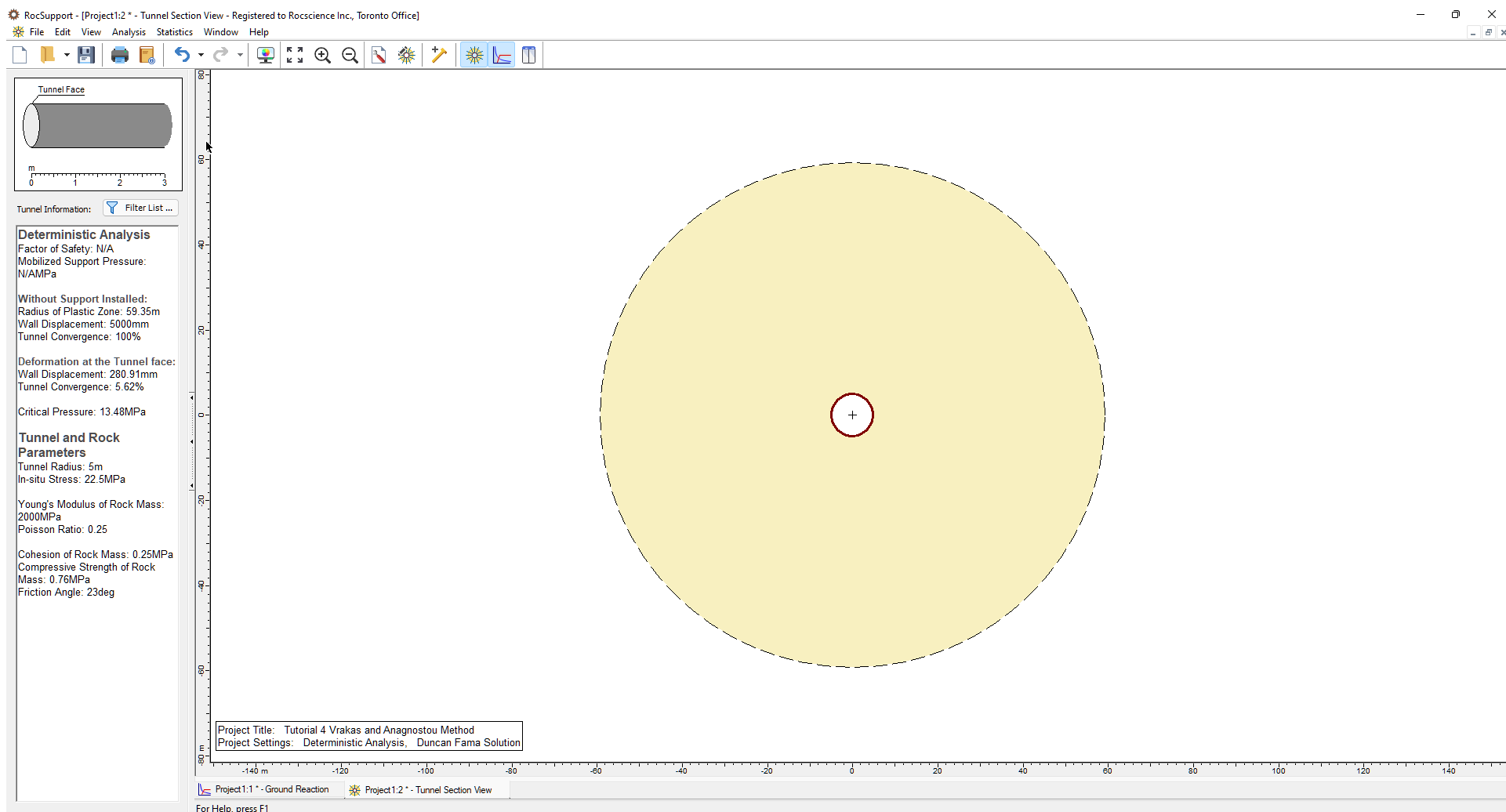
The textbox on the left corner of the screen confirms that the tunnel convergence is 100%. This means that the tunnel walls were displaced by 5 meters (the length of the radius) into the tunnel. Therefore, this problem can clearly be classified as a large-strain problem. We will now see what results we get using the Vrakas and Anagnostou (2014) Solution Method.
3.0 Method 2: Vrakas and Anagnostou
3.1 Project Settings
- Select: Analysis > Project Settings

- In the General tab, change the Solution Method to Vrakas and Anagnostou (2014). Notice the text on the right updates to give a small description of the small strain method. We will assume all input values are exact values (deterministic).
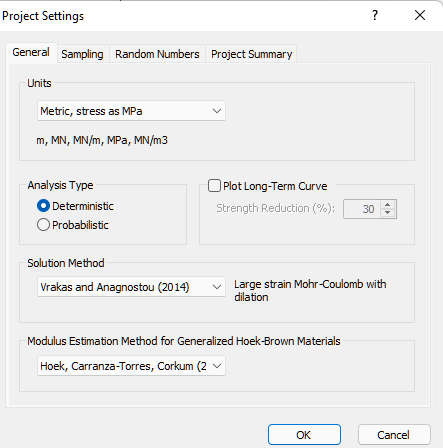
- Click OK.
Immediately the textbox on the left corner of the screen updates the results to show that the tunnel convergence is now approximately 50%. The Ground Reaction curve should look as follows:
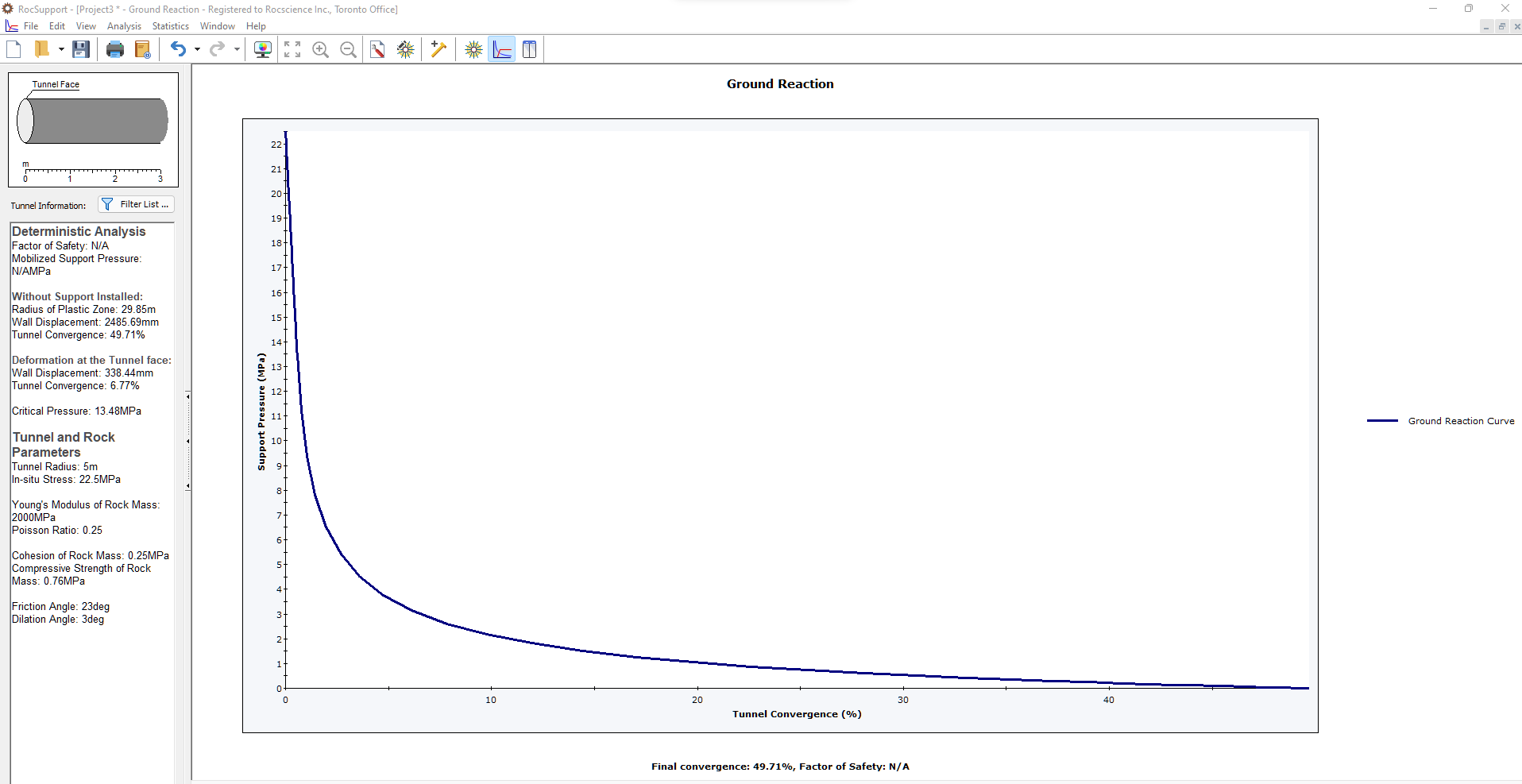
This demonstrates the importance of using the Vrakas and Anagnostou Method for a large strain model.
We will now add support to the tunnel.
4.0 Custom Support
To open the Support Parameters dialog:
- Select: Analysis > Support Parameters

- We will add steelset support to the tunnel. Click on the steelsets tab and check the Add Support box.
- Then click on the Common Types button in the same tab.
- Select the Types button in the tab. You should see the Reinforcement dialog.
- We will apply the type W1100 X 499 steelset. Select OK. The information is now loaded in the dialog.
- Select Apply and Close.
- Switch to the Tunnel Section View
 from the toolbar or the Analysis menu.
from the toolbar or the Analysis menu.
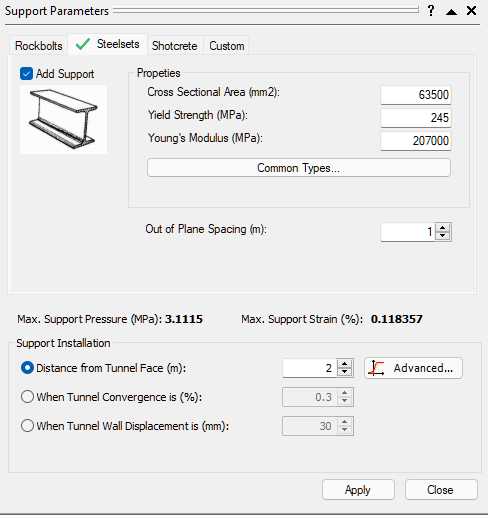
Here, we can define the properties of our custom steelset. Alternatively, we can select a custom support from the table of custom support types.
We can see from the textbox that the radius of the plastic zone has decreased from 30 m to 17 m. The tunnel convergence has also been reduced to 11%.
However, the tunnel will need further reinforcement. This will be left as an exercise to the user.
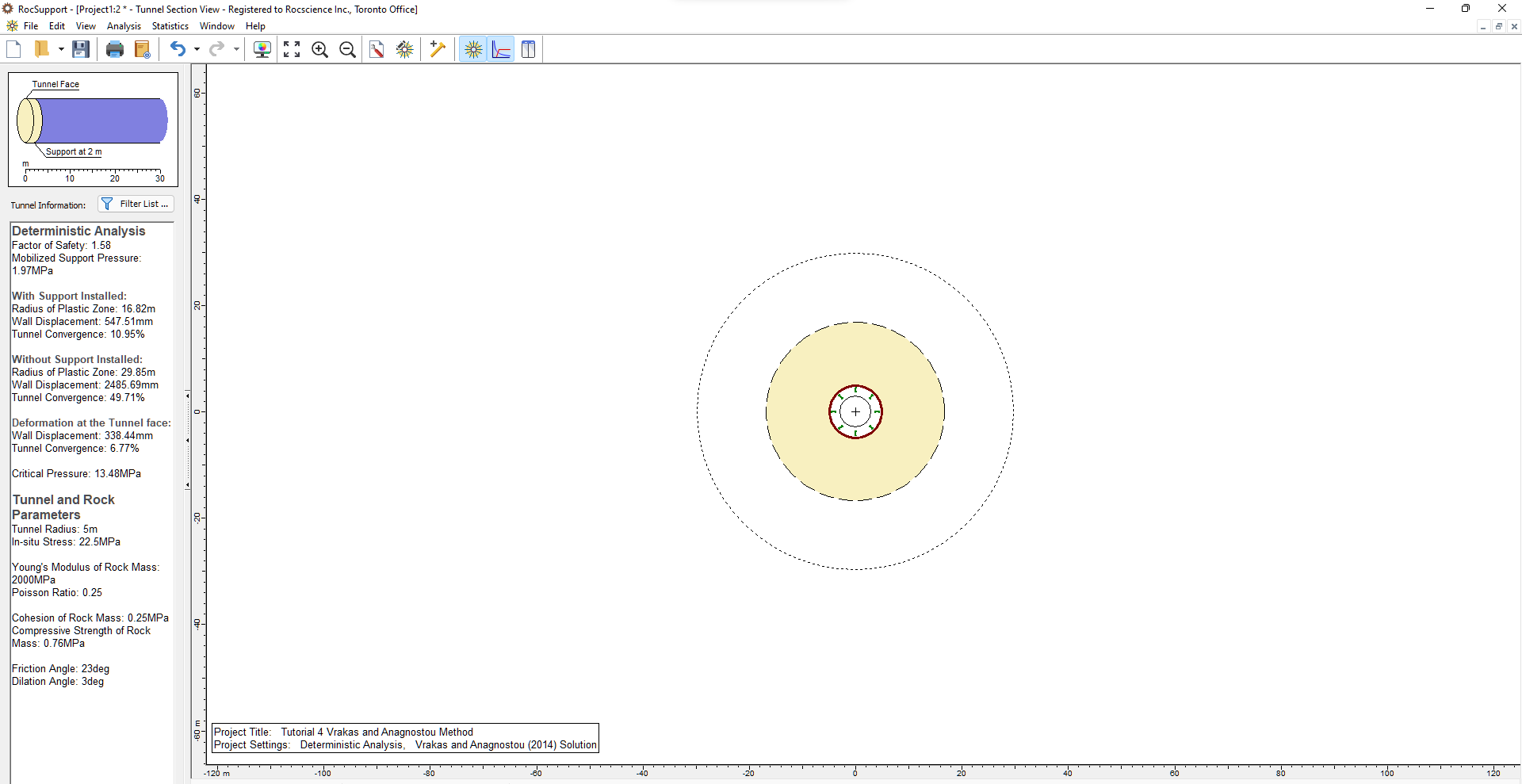
This concludes Tutorial 4 Using the Vrakas and Anagnostou Method.