Joint Shear Strength
If you are performing a Probabilistic analysis with RocPlane, the Joint Shear Strength can be defined as a random variable as follows:
- Select Input Data
 and select the Strength tab in the Probabilistic Input Data dialog.
and select the Strength tab in the Probabilistic Input Data dialog. - Select the Shear Strength Model (e.g., Mohr-Coulomb, Barton-Bandis, Power Curve).
- Select the method of defining shear strength as a random variable from the Random Variables drop-down: Parameters or Strength (see definitions below).
- Enter the probabilistic shear strength parameters as described below.
Random Variables = Parameters
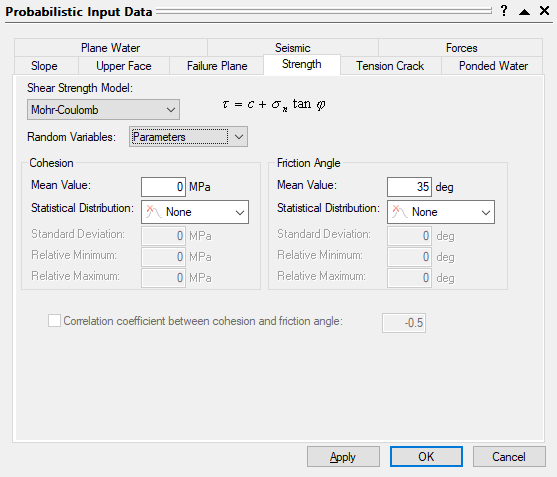
If Random Variables = Parameters, you can define a Statistical Distribution for each parameter used in the strength criteria.
CORRELATION COEFFICIENT
If you are using the Mohr-Coulomb as the Shear Strength Model, you can define a Correlation coefficient between cohesion and friction angle. For details, see Correlation Coefficient in a RocPlane Probabilistic Analysis.
If you are using Barton-Bandis or Power Curve as the Shear Strength Model, then you CANNOT define a correlation between the statistical sampling of the strength parameters (i.e., the statistical sampling of each parameter is performed independently of the sampling of any other random variables).
Random Variables = Strength
If Random Variables = Strength, the shear strength (tau) is defined directly as a random variable rather than defining the individual parameters of the strength criterion as random variables. For a given normal stress, a random value of shear strength is generated. This works as follows:
- Set the Random Variables = Strength.
- Enter the mean values of the strength criterion parameters (e.g., Cohesion and Friction Angle for the Mohr-Coulomb criterion).
- Choose a Statistical Distribution for the shear strength. Only Lognormal and Gamma distributions are allowed because these distributions are only defined for positive values and therefore ensure that randomly generated values of shear strength are always positive.
- Enter the Coefficient of Variation for the shear strength. The Coefficient of Variation is equal to the standard deviation divided by the mean shear strength.
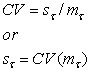
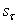 = standard deviation of shear strength,
= standard deviation of shear strength, 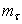 = mean shear strength.
= mean shear strength.NOTE: Typical values of shear strength CV range from 0.15 to 0.35 [Miller et.al. (2000)].
- When the analysis is computed, random values of shear strength are generated as follows:
- The normal stress on a joint plane is computed.
- Using the mean values of the strength criterion parameters (e.g. cohesion and friction angle), the mean shear strength is calculated. This defines a point on the mean strength envelope.
- Using the mean shear strength, coefficient of variation, and the selected statistical distribution (Lognormal or Gamma), a random value of shear strength is generated, for the given normal stress. This will be the actual value of shear strength used in the RocPlane safety factor calculation.
- The above steps are repeated for each probabilistic simulation until the required number of samples are generated.
The random shear strength option is schematically illustrated in the following figure for the Mohr-Coulomb criterion. Essentially, you are defining a variability of shear strength about the mean strength envelope. This is intuitively simpler to grasp than defining variability of individual strength parameters.
The random shear strength option is particularly useful for Barton-Bandis or Power Curve strength models, since it eliminates the need for defining statistical distributions for individual strength parameters (which may be difficult to obtain or unavailable). Furthermore, the issue of statistical correlation of the strength parameters is avoided (i.e., you do not have to worry about generating unrealistic combinations of strength parameters, since variability is defined with respect to the mean envelope).
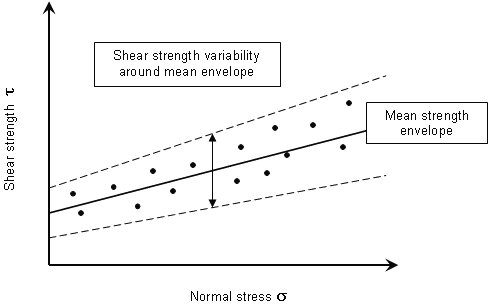
Random shear strength option (Mohr-Coulomb envelope)